Contexte : Premier pas d'un jeune bachelier en Architecture
Jean est un lauréat du baccalauréat série C, il se propose d'utiliser ses connaissances pour l'élaboration du plan et de la décoration de la nouvelle maison que son père projette de construire. Dans ses préoccupations, il suggère la construction d'une paillote dont le plancher aura la forme de l'ensemble $(\sum)$ des points $M$ du plan tels que : $MF+MF'\leq 5$ où $F\ $ et $\ F'$ sont deux points distincts données du plan, matérialisé par le plancher (unité de longueur $1\,m$). La toiture de cette paillote aura la forme d'une pyramide de sommet $S.$
Jean se propose également de dessiner le motif décoratif du mur de la clôture de la maison. Son père veut en savoir un peu plus sur ses intentions. Pour satisfaire la curiosité de son père, Jean a choisi dans le plan du sol un point $O$, puis il a défini un repère orthonormé direct $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ de l'espace tel que le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ soit un repère du plan du plancher.
Dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$, Jean a choisi $F\left(\dfrac{3}{2}\ ;\ 0\right)$ et $F'\left(\dfrac{-3}{2}\ ;\ 0\right)$ et a tracé l'ensemble $(\Gamma)$ des points $M$ tels que $MF+M'F=5.$ Jean explique que dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$, les coordonnées du point $S$ seront des entiers naturels.
Tâche :
Tu es invité (e) à résoudre les problèmes suivants en vue de te faire une idée plus précise du projet de Jean.
Problème 1
1. a) Justifie que $(\Gamma)$ est une ellipse.
b) Précise le centre et l'excentricité de $(\Gamma).$
c) Détermine une équation de $(\Gamma)$ dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
2. a) Précise les coordonnées des sommets de $(\Gamma).$
b) Trace $(\Gamma).$
c) Explique comment Jean a pu tracer $(\Gamma)$ sur le plancher.
Problème 2
Jean a expliqué que deux faces de la pyramide représentant la toiture de la paillote sont contenues dans les plans $(\mathcal{P_{1}})\ $ et $\ (\mathcal{P_{2}})$ d'équations respectives : $x+2y+2z-16=0\ $ et $\ 11x+9y−2z−19=0$ dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}).$
3. a) Démontre que $(\mathcal{P_{1}})\ $ et $\ (\mathcal{P_{1}})$ sont sécants suivant une droite $(\Delta).$
b) Démontre que si $M(x\ ;\ y\ ;\ z)$ est un point de $(\Delta)$ alors : $12x+11y=35.$
c) Résoudre dans $\mathbb{Z^{2}}$ l'équation $12x+11y=35$ d'inconnus $(x\ ;\ y).$
d) Détermine les points de $(\Delta)$ dont toutes les trois coordonnées sont entiers relatifs.
4. a) Détermine les coordonnées du point $S.$
b) Calcule du point $S$ au plan du plancher.
Problème 3
La figure ci-dessous représente une partie du motif de la décoration que propose Jean pour le mur de la clôture.
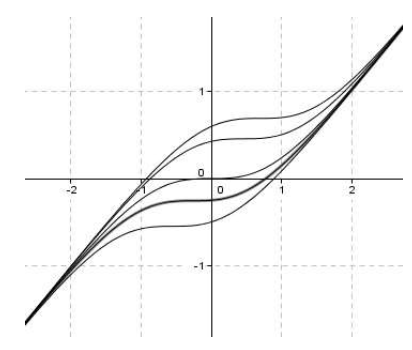
Il l'a obtenu en représentant dans un repère orthonormé $($Unité $2\,cm)$ quelques courbes de la famille de courbes $(\mathcal{C_{k}})$ représentatives des fonctions :
$$\begin{array}{rcl} f_{k}\ :\ \mathbb{R}&\longrightarrow&\mathbb{R}\\ x&\longmapsto& x+\dfrac{1-k\mathrm{e^{2x}}}{1+k\mathrm{e^{2x}}} \end{array}$$
5. a) Justifie que l'ensemble de définition de $f_{k}$ est $\mathbb{R}.$
b) Détermine les limites de $f_{k}$ aux voisinages de $-\infty$ et $+\infty.$
6. a) Justifie que les fonctions $f_{k}$ sont solutions de l'équation différentielle : $y'=(y−x)^{2}.$
b) Justifie que les fonctions dérivées $f'_{k}$ des fonctions $f_{k}$ s'annulent pour un seul nombre $x_{k}$ que tu préciseras.
c) Détermine le sens de variation de $f_{k}.$
d) Dresse le tableau de variation de $f_{k}.$
7. Soit $A_{k}$ le point de $\left(\mathcal{C_{k}}\right)$ d'abscisse $x_{k}.$
a) Précise les coordonnées de $A_{k}.$
b) Justifie que tous les points $A_{k}$ appartiennent tous à une même droite.
8. a) Démontre que pour tout nombre réel $x$ :
i. $f_{k}(x)=x-1+\dfrac{2}{1+k\mathrm{e^{2x}}}$
ii. $f_{k}(x)=x+1-\dfrac{2k\mathrm{e^{2x}}}{1+k\mathrm{e^{2x}}}$
b) Démontre que les droites $\left(\Delta_{1}\right)$ et $\left(\Delta_{2}\right)$ d'équations respectives $y=x+1$ et $y=x-1$ sont des asymptotes aux $\left(\mathcal{C_{k}}\right).$
c) Étudie la position relative des $\left(\mathcal{C_{k}}\right)$ par rapport aux droites $\left(\Delta_{1}\right)$ et $\left(\Delta_{2}\right).$
9. a) Détermine la valeur de $k$ pour laquelle $\left(\mathcal{C_{k}}\right)$ passe par l'origine du repère.
b) Trace les courbes $\left(\mathcal{C_{\dfrac{1}{4}}}\right)$, $\left(\mathcal{C_{1}}\right)$ et $\left(\mathcal{C_{3}}\right)$ dans le même repère.
10. Jean propose de compléter son motif en traçant les courbes $\left(\Gamma_{k}\right)$ d'équations : $x=f_{k}(y−1).$
a) Justifie que les fonctions $f_{k}$ sont des bijections.
b) Soit $f_{k}^{-1}$ les bijections réciproques des $f_{k}.$
Étudie la dérivabilité de $f_{k}^{-1}.$
c) Démontre que les courbes $\left(\Gamma_{k}\right)$ sont les images des courbes $\left(\mathcal{C_{k}}\right)$ par une isométrie plane $\mathcal{s}.$
d) Caractérise $\mathcal{s}.$


Ajouter un commentaire