Bac Maths C et E, Benin 2017

 

Sur un domaine $AFED$ de forme rectangulaire, Arouna, le propriétaire décide d'ériger une maison. Dans le dossier technique, l'architecte en charge du projet propose un aménagement comme l'indique la figure ci-dessous :

 

 

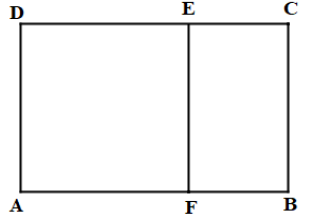
La partie représentée par le carré $AFED$ est destinée au bâtiment et l'autre partie au jardin et autres ouvrages. L'architecte affirme que pour réaliser le découpage du domaine, il a utilisé une similitude direct $y$ qui transforme les points $A$, $B$, $C$ et $D$ respectivement en $B$, $C$, $E$ et $F.$

 

N'étant pas outillé pour comprendre le dossier, Arouna sollicite son fils Ousmane, élève en terminale $C$, pour mieux apprécier certaines informations qui y sont contenues. Afin de vérifier l'existence de la similitude $y$, Ousmane suppose que $AD=1$ et $AB=l\ (l>1)$, puis il munit le plan du repère orthonormé $(A\;,\ \overrightarrow{AF}\;,\ \overrightarrow{AD}).$

 

Il s'intéresse par ailleurs à la quantité de carreaux à utiliser pour le revêtement du plancher dans les pièces du bâtiment et aussi à la configuration du jardin.

Tu es invité(e) à aider Ousmane à répondre à ses différentes préoccupations en résolvant les problèmes ci-dessous.

1. Ousmane suppose que la similitude $y$ existe.

 

a) Démontre que l'on a : $\dfrac{1}{l}=l-1$

 

b) Déduis-en que : $l=\dfrac{1+\sqrt{5}}{2}.$

 

c) Détermine le rapport et l'angle de la similitude $y.$

 

2. a) Justifie l'existence d'une similitude directe $y'$ qui transforme $A$ en $B$ et $B$ en $C.$

 

b) Démontre que dans le repère $(A\;,\ \overrightarrow{AF}\;,\ \overrightarrow{AD})$, la similitude $y'$ a pour écriture complexe : $z'=\dfrac{\sqrt{5}-1}{2}\mathrm{i}z+\dfrac{\sqrt{5}+1}{2}.$

 

c) Détermine les images des points $C$ et $D$ par $y'.$

 

d) Justifie que l'architecte a raison au sujet du procédé de découpage du domaine.

Il est prévu que le plancher des pièces du bâtiment seront carrelés.

 

3. Le plancher de la salle à manger a la forme d'un rectangle dont les dimensions sont : $4.54\,m$ et $3.75\,m.$ 

 

On veut carreler cette pièce avec des carreaux carrés de $33\,cm$ de côté. 

 

On commence la pose à partir d'un coin de la pièce.

 

a) Justifie que qu'il n'est pas possible de couvrir le plancher de cette pièce avec uniquement des carreaux entiers (sans découpe).

 

b) Effectue la division euclidienne de $454$ par $33.$ 

 

Déduis-en le nombre de carreaux non découpés qui sont posés dans le sens de la longueur.

 

c) Détermine le nombre de carreaux non découpés qui seront posés dans cette pièce.

 

4. Le plancher de la cuisine a la forme d'un rectangle de dimension $4.55\,m$ et $3.85\,m.$

 

On veut utiliser deux types de carreaux pour son revêtement : des pièces carrées de type $T_{1}$ de $15\,cm$ de côté et des pièces carrées de type $T_{2}$ de $35\,cm$ de côté ; on doit utiliser plus de pièces de type $T_{2}$ que de pièces de type $T_{1}.$

 

a) Justifie que le nombre $a$ de carreaux du type $T_{1}$ et le nombre $b$ de carreaux du type $T_{2}$ sont tels que : $9a+49b=7007.$

 

b) Résous dans $\mathbb{Z^{2}}$ l'équation $9a+49b=7007.$

 

c) Détermine le nombre de pièces de chaque type que l'on peut poser dans la cuisine.

Pour rendre attrayante la cour de la maison, l'architecte a prévu un parterre de fleurs suivant des configurations bien précises. L'une des configurations est modélisée par une portion $(\Gamma)$ de l'ensemble des points $M$ dont les coordonnées $(x\ ;\ y)$ dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$ Vérifient : $\dfrac{3\ln y}{\sqrt{y}}+y-1-|x|=0.$

 

5. On considère la fonction $g$ définie sur $]0\ ;\ +\infty[$ par $g(x)=2x\sqrt{x}-3\ln x+6.$

 

a) Étudie le sens de variation de $g.$

 

b) Justifie que $g$ admet un minimum que tu préciseras.

 

c) Détermine le signe de $g(x)$ pour tout $x$ élément de l'intervalle $]0\ ;\ +\infty[.$

 

6. On considère la fonction $f$ de $]0\ ;\ +\infty[$ vers $\mathbb{R}$ définie par : $f(x)=\dfrac{3\ln x}{\sqrt{5}}+x-1.$

 

a) Démontre que $f$ est une application.

 

b) Étudie les limites de $f$ à droite en $0$ et en $+\infty.$

 

c) Étudie le sens de variation de $f.$

 

d) Dresser le tableau de variation de $f.$

 

e) Déduis-en le signe de $f(x)$ pour tout $x$ élément de $]0\ ;\ +\infty[.$

 

7. On note $(\mathcal{C})$ la courbe de $f$ dans le plan muni du repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}).$

 

a) Démontre que la droite $(\mathcal{D})$ d'équation $y=x-1$ est asymptote à $(\mathcal{C}).$

 

b) Étudie la position relative de $(\mathcal{C})$ et $(\mathcal{D}).$

 

c) Trace la courbe $(\mathcal{C}).$

 

8. a) Démontre que $f$ est une bijection. 

 

On note $(\mathcal{C'})$ la courbe représentative de sa bijection réciproque.

 

b) Soit $M(x\ ;\ y)$ un point de $(\Gamma).$ 

 

En remarquant que $f(y)=|x|$, démontre que $y\geq 1.$

 

c) Démontre que $(\Gamma)$ est la réunion d'une portion $(\Gamma_{1})$ de $(\mathcal{C'})$ et son symétrique par rapport à l'axe des ordonnées.

 

d) Trace $(\Gamma)$ dans le même repère que $(\mathcal{C}).$