Bac Maths D, Cameroun 2018
Exercice 1
1. On considère $a$ et $b$ deux réels, avec $a$ non nul.
Démontrer que les fonctions de la forme $x\mapsto C\mathrm{e}^{ax}-\dfrac{b}{a}$ où $c$ est un réel, sont de solutions de l'équation différentielles : $y'=ay+b\ (E)$ (on admettra par la suite que ce sont les seules).
2. Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse.
a) Affirmation 1 :
Si une fonction $f$ définie sur l'ensemble des nombres réels $\mathbb{R}$ est solution de l'équation différentielle $y'+3y=6$, alors la courbe représentant $f$ admet une asymptote horizontale en $+\infty$
b) Affirmation 2 :
Si une fonction $f$ définie sur l'ensemble des nombres réels $\mathbb{R}$ est solution de l'équation différentielle $y'=y$, alors pour tous réels $\alpha$ et $\beta$ :
$$f(\alpha+\beta)=f(\alpha)\times f(\beta)$$
c) Affirmation 3 :
La courbe d'une fonction solution de l'équation différentielle $y'=-2y$ coupe l'axe des ordonnées au point d'ordonnée $3/2$ (voir figure ci-dessous).
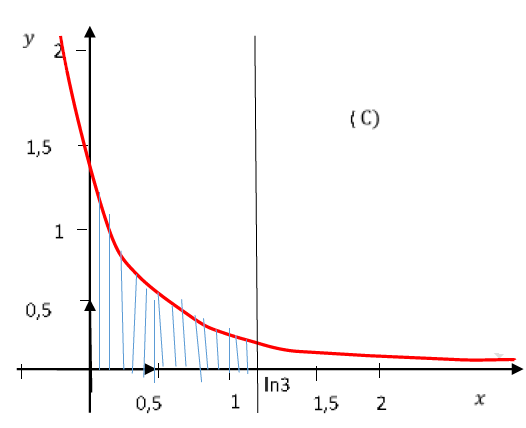
L'aire, en unité d'aire, du domaine délimité par l'axe des abscisses, la courbe et les droites d'équations respectives $x=0\text{ et }x\ln 3\text{ est }3/2$
Exercice 2
Le plan complexe est muni d'un repère orthonormé $\left(O\;,\ \overrightarrow{OI}\;,\ \overrightarrow{OJ}\right).$
On considère les points $A$ et $B$ d'affixes respectives : $z_{A}=2\text{ et }z_{B}=\dfrac{3}{2}+\mathrm{i}$
On considère les points $M$, $N$ et $P$ tels que les triangles $AMB$, $BNO$ et $OPA$ soient des triangles rectangles isocèles de sens direct comme le montre la figure ci-dessous.
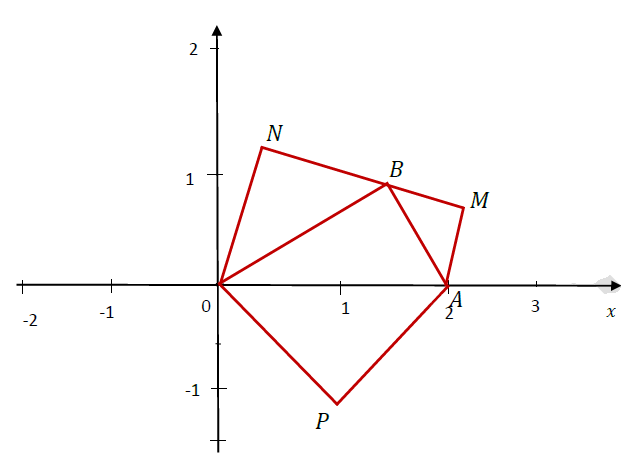
On note $S_{1}$ la similitude directe de centre $A$ qui transforme $M$ en $B.$
On note $S_{2}$ la similitude directe de centre $O$ qui transforme $B$ en $N.$
Le but de cet exercice est de démontrer que les droites $(OM)$ et $(PN)$ sont perpendiculaires.
1) Donner l'angle et le rapport de $S_{1}$ et $S_{2}.$
2) a) En utilisant les résultats de la question 1) donner les écritures complexes de $S_{1}$ et $S_{2}.$
b) En déduire les affixes $z_{M}$ et $z_{N}$ des points $M$ et $N.$
c) Donner par lecture graphique, l'affixe $z_{P}$ du point $P$, puis démontrer que les droites $(OM)$ et $(PN)$ sont perpendiculaires.
Exercice 3 : Problème
On considère la fonction numérique $f$ définie sur $\mathbb{R}$ par : $$f(x)=2x+1-x\mathrm{e}^{x-1}$$
On note $(\mathcal{C})$ sa courbe représentative dans le plan muni d'un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j}).$
A. Étude de la fonction $f$ et construction de la courbe $(\mathcal{C})$
1. Étudier la limite de la fonction $f$ en $-\infty$ puis en $+\infty$
$\left(\text{On poura écrire }x\mathrm{e}^{x-1}=\dfrac{1}{\mathrm{e}}x\mathrm{e}^{x}\right)$
2. Démontrer que la droite $\Delta$ d'équation $y=2x+1$ est asymptote à la courbe $(\mathcal{C})$ en $-\infty$ et préciser la position de la courbe $(\mathcal{C})$ par rapport à la droite $\Delta.$
3. a) Calculer la dérivée $f'$ et la dérivée seconde $f''$ de $f.$
b) Dresser le tableau de variation de la fonction $f$ en précisant les limites de la fonction $f'$ en $-\infty$ et en $+\infty.$
c) Calculer $f'(1)$ et en déduire le signe de $f'$ pour tout réel $x.$
d) Dresser le tableau de variation de la fonction $f$
4. Soit $I$ l'intervalle $[1\;,\ 9\;,\ 2].$
Démontrer que sur $I$, l'équation $f(x)=0$ a une solution unique $\alpha.$
5. Tracer la droite $\Delta$ et la courbe $(\mathcal{C})$ $($unité graphique : $2\,cm).$
B. Recherche d'une approximation de $\alpha.$
On considère la fonction $g$ définie sur l'intervalle $I$ par : $$g(x)=1+\ln\left(2+\dfrac{1}{x}\right)$$
1. Démontrer que, sur $I$, l'équation $f(x)=0$ équivaut à l'équation $g(x)=x.$
2. Étudier le sens de variation de la fonction $g$ sur $I$ et démontrer que, pour tout $x$ appartenant à $I$, $g(x)$ appartient à $I.$
3. Démontrer que, pour tout $x$ de l'intervalle $I$, $g(x)\leq \dfrac{1}{9}$
4. Soit $\left(U_{n}\right)$ la suite des nombres réels définie par : $U_{0}=2$ et pour tout $n$, $U_{n+1}=g\left(U_{n}\right).$
On déduit de la question B.2. que tous les termes de cette suite appartiennent à l'intervalle
I. On ne demande pas de le démontrer.
a) Démontrer que, pour tout $n$, $\left|U_{n+1}-\alpha\right|\leq\dfrac{1}{9}\left|U_{n}-\alpha\right|$
b) En déduire, en raisonnant par récurrence, que : pour tout $n$ de $\mathbb{N}$
$$\left|U_{n}-\alpha\right|\leq\left(\dfrac{1}{9}\right)^{n}\times\dfrac{1}{10}$$
d) En déduire que la suite $\left(U_{n}\right)$ converge et préciser sa limite.

Ajouter un commentaire