Bac Physique chimie 1er groupe S2 S2A S4 S5 2019
Exercice 1 (4 points)
Un groupe d'élèves se propose de synthétiser l'arome tout en suivant l'évolution de la réaction au cours du temps.
Pour ce faire, il dispose, dans le laboratoire de leur lycée, de deux flacons de liquides dont les étiquettes portent les indications ci-dessous
Flacon 1 : Solution d'acide éthanoïque ; pourcentage en masse d'acide pur $57.10\%$ ; densité $1.05$
Flacon 2 : Propan-1-ol pur ; masse volumique : $803\;kg\cdot m^{-3}.$
Le groupe prélève des volumes $V_{1}$ et $V_{2}$ respectivement de propan-1-ol et d'acide éthanoïque de façon à réaliser un mélange de $0.6 \;mol$ de propan-1-ol et $0.6\;mol$ d'acide éthanoïque et y ajoute quelques gouttes d'acide sulfurique.
Le mélange est chauffé à reflux.
1.1 Donner le nom de la réaction qui se produit dans le mélange et préciser ses caractéristiques. (0.5 point)
1.2 Écrire l'équation-bilan de cette réaction en utilisant les formules semi-développées.
Nommer l'arôme synthétisé. (0.5 point)
1.3 Déterminer les volumes $V_{1}$ et $V_{2}$ initialement mélangés. (0.5 point)
1.4 Par une méthode appropriée, les élèves déterminent à divers instants $t$, le nombre de moles $n$ d'acide éthanoïque restant.
Les valeurs obtenues sont consignées dans le tableau ci-après :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{t(min)}&0&10&20&30&40&50&60&70&80&90\\ \hline \text{n(mol)}&0.60&0.45&0.33&0.26&0.23&0.21&0.20&0.20&0.20&0.20\\ \hline \end{array}$$
1.4.1 Tracer la courbe $n=f(t).$
Échelles : $1\;cm$ pour $0.05\;mol$ et $1\;cm$ pour $10\;min$ (0.5 point)
1.4.2 Déterminer graphiquement la vitesse de disparition de l'acide éthanoïque à chacune des dates suivantes :
$t_{1}=25\;min$ ; $t_{2}=40\;min$ ; $t_{3}=75\;min.$
Comparer ces vitesses. (01 point)
1.4.3 Préciser la date à laquelle l'équilibre est atteint.
Déterminer à cet instant le pourcentage d'acide ayant réagi. (0.5 point)
1.4.4 Quel est l'intérêt de procéder à un chauffage à reflux pour synthétiser l'arôme ?
Quel est le rôle joué par l'acide sulfurique ? (0.5 point)
On donne les masses molaires en $g\cdot mol^{-1}$ : $M(C)=12$ ; $M(O)=16$ ; $M(H)=1$
Exercice 2 (04 points)
Il intervient également dans la préparation de fibres synthétiques.
2.1 Une masse de $146\;g$ de diméthylformamide contient $28\;g$ d'azote.
2.1.1 Montrer que la formule brute du diméthylformamide est $C_{3}H_{7}ON.$ (0.5 point)
2.1.2 Écrire les formules semi-développées possibles des amides compatibles avec cette formule brute et donner leurs noms. (01 point)
2.1.3 Sachant que le diméthylformamide possède deux groupes méthyles liés à un même atome, identifier cet amide en précisant sa formule semi-développée et son nom dans la nomenclature officielle. (0.5 point)
2.2 Pour synthétiser cet amide, on dispose des produits suivants :
chlorure de thionyle $(SOCl_{2})$ ;
oxyde de phosphore $(P_{4}O_{10})$ , acide méthanoïque, acide éthanoïque, acide propanoïque, ammoniac, méthylamine, éthylamine, diméthylamine.
2.2.1 Proposer deux méthodes de synthèse rapides et totales du diméthylformamide.
Préciser pour chaque méthode de synthèse les produits utilisés.
2.2.2 Écrire les équation-bilans des réactions correspondant à chaque méthode. (01 point)
On donne les masses molaires atomiques en $g\cdot mol^{-1}$ : $M(C)=12$ ; $M(O)=16$ ; $M(N)=14$ ; $M(H)=1$
Exercice 3 (04 points)
Huit ans plus tard la sonde d'exploration s'est posée sur Titan le plus gros des satellites de Saturne.
Le tableau ci-dessous rassemble les données relatives à Titan et à trois autres satellites de Saturne.
$$\begin{array}{|c|c|c|c|} \hline \text{Satellite}&\text{Distance moyenne}&\text{Période de}&\text{Rapport}\dfrac{T^{2}}{r^{3}}\\ &\text{au centre de}&\text{révolution }T&\\ &\text{Saturne r (en km)}& &\\ \hline \text{Janus}&159\cdot10^{3}&17\;h\ 38\;min&\\ \hline \text{Encelade}&238\cdot10^{3}&1\;j\ 8\;h\ 53\;min&\\ \hline \text{Dione}&377\cdot10^{3}&2\;j\ 17\;h\ 41\;min&\\ \hline \text{Titan}&1220\cdot10^{3}&15\;j\ 22\;h\ 41\;min&\\ \hline \end{array}$$
3.1 On s'intéresse à l'étude du mouvement d'un satellite supposé ponctuel de masse $m$ en orbite circulaire de rayon $r$ autour de Saturne.
Le mouvement est étudié dans un référentiel lié à Saturne qui sera considéré comme un référentiel galiléen.
On suppose que le satellite est soumis à la seule action de Saturne.
On assimile Saturne à un corps sphérique de masse $M$ possédant une répartition sphérique de masse.
3.1.1 Après avoir rappelé la loi de la gravitation universelle, faire un schéma où seront représentés Saturne, le satellite et la force de gravitation exercée par Saturne sur le satellite.
On notera $k$, la constante de gravitation et on prendra $k=6.67\cdot10^{-11}N\cdot m^{2}\cdot kg^{-2}.$ (0.5 point)
3.1.2 Par application de la deuxième loi de Newton déterminer les caractéristiques du vecteur accélération du mouvement du satellite. (0.5 point)
3.1.3 Montrer que le mouvement du satellite est uniforme. (0.25 point)
3.1.4 Établir la relation entre la période de révolution $T$ du satellite et le rayon $r$ de sa trajectoire. (0.25 point)
3.2 Recopier le tableau ci-dessus et le compléter par les valeurs du rapport $\dfrac{T^{2}}{r^{3}}.$
La $3^{ième}$ loi de Kepler est-elle vérifiée ? (0.75 point)
NB :
3.3 Déterminer la masse $M$ de Saturne. (0.5 point)
3.4 On définit l'énergie potentielle d'interaction gravitationnelle $E_{p}$ entre Saturne et le satellite par :
$\dfrac{dE_{p}}{dr}=F(r)$ ; relation où $F(r)$ est l'intensité de la force de gravitation que l'un exerce sur l'autre.
3.4.1 En choisissant $E_{p}=0$ quand $r$ tend vers l'infini, déterminer l'expression de $E_{p}$ (0.5 point)
3.4.2 Comparer l'énergie potentielle $E_{p}$ avec l'énergie cinétique $E_{c}$ du satellite. (0.25 point)
3.4.3 Déterminer l'énergie mécanique totale $E_{m}$ du satellite en fonction de $k$, $M$, $m$ et $r.$
La calculer pour Titan de masse $m=1.35\cdot10^{23}kg.$ (0.5 point)
Exercice 4 (04 points)
$E_{n}=\dfrac{-E_{0}(eV)}{n^{2}}$ où $n$ est un entier tel que $n\geq 1$ et $E_{0}=13.6.$
Le diagramme de la figure 1 (page suivante) représente sans souci d'échelle quelques niveaux d'énergie de l'atome d'hydrogène.
4.1 Comment qualifie-t-on l'état dans lequel se trouve l'atome d'hydrogène lorsque $n=1$ ?
lorsque $n>1$ ? (0.5 point)

Exercice 5 (04 points)
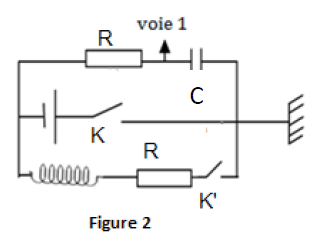
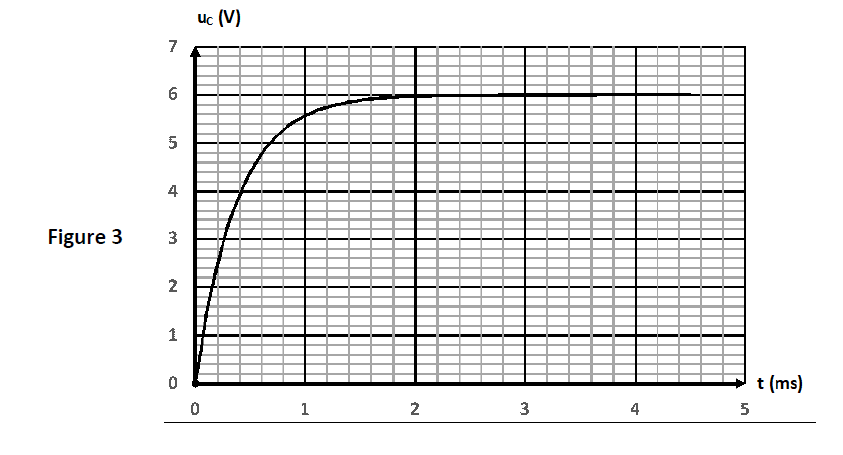
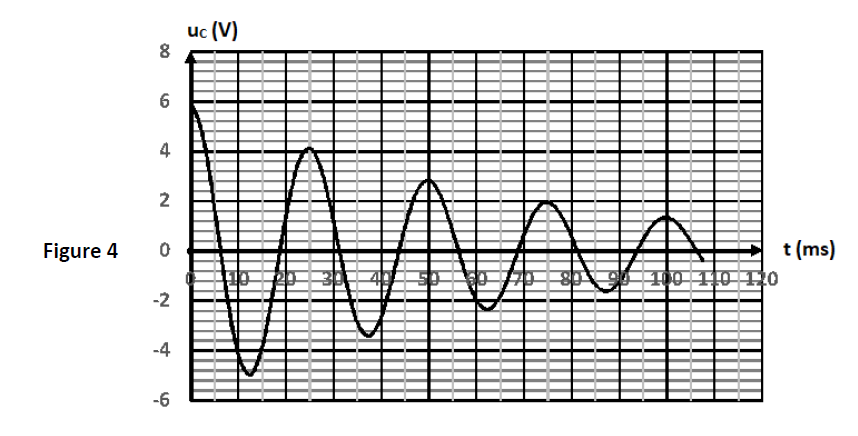

Ajouter un commentaire