Corrigé Bac Maths S1 S3 1er groupe 2008
Exercice 1
1) En désignant par b le terme central de la progression arithmétique et par r sa raison, on peut écrire : a=b−r et c=b+r.
Les autre données se traduisent alors par :
{∑k∈{−1, 1, 2}p(X=k)=1E(X)=1
c'est à dire {ea+eb+ec=11.ea−1.eb+2.ec=1soit{ebe−r+eb+eber=1ebe−r−eb+2.eber=1
En faisant la différence membre à membre et en simplifiant par eb, on trouve er=2 soit r=ln2.
La première équation devient alors :
(12+1+2) c'est à dire eb=27 ⇒ b=ln27
Ensuite a=b−r=ln27−ln2 ⇒ a=ln17
Et c=b+r=ln27+ln2 ⇒ c=ln47
Pour calculer la variance, calculons d'abord E(X2).
E(X2)=12.ea+(−1)2.eb+22.ec=17+27+447=197
Alors
V(X)=E(X2)−(E(X))2=197−1⇒ V(X)=127
2) a) xG=17(1.xA+2xB+4xC)=1 donc G=A
b) φ(G)=17[→GA2+2→GB2+4→GC2]
Soit, en se souvenant que G=A :
φ(G)=17[2→AB2+4→AC2]=17(2.4+4.1)⇒ φ(G)=127=V(X)
On peut écrire en utilisant la relation de Schales et en développant :
φ(M)=17[(→MG+→GA)2+2(→MG+→GB)2+4(→MG+→GC)2]=17[→MG2+→GA2+2→MG.→GA+2(→MG2+→GB2+2→MG.→GB)+4(→MG2+→GC2+2→MG.→GC)]=→MG2+17[→GA2+2→GB2+4→GC2]+17.2→MG[→GA+2→GB+4→GC]
Le troisième du second membre est nul parce que G est le barycentre du système {(A, 1), (B, 2), (C, 4)}.
Donc, φ(M)=→MG2+φ(G)
La relation φ(G)=3 est alors équivalente à : →MG2=97 ou MG=3√77
Par conséquent
(Γ)={M1, M2} où M1 et M2 sont les deux points de (Δ) dont la distance au point A est −3√77 et 3√77
Exercice 2
1) a) On a, pour tout réel x compris entre k et k+1 : 1k+1≤1x≤1k.
Puis en intégrant : ∫k+1k1k+1dx≤∫k+1kdx≤∫k+1k1x1kdx
c'est à dire 1k+1≤∫k+1k1xdx≤1k+1
b)
∫k+1k1xdx=[lnx]k+1k=ln(k+1)−lnk=lnk+1k=1k−f(k)
2) a) En réduisant le deuxième membre au même dénominateur, on obtient : ax+bx+1=(a+b)x+ax(x+1)
Donc a et b sont tels que ∀x≠0 et −1.
Alors a+b=0 et a=1; ce qui entraîne b=−1
Par conséquent 1x(x+1)=1x−1x+1
b) Soit
Un=2n∑k=n1k(k+1)=2n∑k=n[1k−1k+1]=2n∑k=n[αk−αk+1]avec αk=1k
Donc en procédant à une itération :
Un=αn−α2n+1=n+1n(2n+1)
Ensuite limn↦+∞Un=0
c) Dans les inégalités de la question 1) a), remplaçons l'intégrale par sa valeur tirée de la question 1) b) 1k+1≤1k−f(k)≤1k.
ce qui permet d'encadrer f(k) :
0≤f(k)≤1k−1k+1
Puis sommons membre à membre ces inégalités depuis k=n à 2n, on obtient la relation demandée :
0≤2n∑k=nf(k)≤2n∑k=n1k−1k+1=Un
Comme limn↦+∞Un=0, le théorème des gendarmes permet de conclure que limn↦+∞2n∑k=nf(k)=0
d) La relation établie dans la question 1.b. donne par sommation :
2n∑k=n∫k+1kdxx=2n∑k=n1k−2n∑k=nf(k)
ou en faisant intervenir la relation de Schales pour les intégrales : ∫2n+1ndxx=Sn−2n∑k=nf(k)
Ensuite en intégrant : ln(k−1)−lnk=Sn−∑2nk=nf(k)
Finalement 2n∑k=nf(k)=Sn−ln2n+1n
Puisque limn↦+∞∑2nk=nf(k)=0 et limn↦+∞ln2n+1n=ln2, on en déduit que limn↦+∞Sn=ln2
Exercice 3
a)
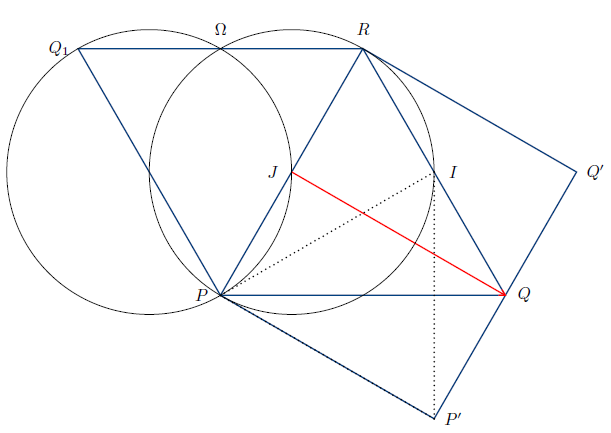
Le point P′ est tel que f(P)=t∘r(P)=t(P)=P′.
Donc le point P′ est entièrement défini par la relation →PP′=→JQ;
P′ est tel que JPP′Q soit un parallélogramme.
Le point Q′ est tel que f(Q)=t∘r(Q)=t(R)=Q′.
Donc le point Q′ est entièrement défini par la relation →RQ′=→JQ;
Q′ est tel que JQQ′R soit un parallélogramme.
b) La droite (IJ) est une droite des milieux pour le triangle PQR, donc JIR a même nature que PQR :
JIR est équilatéral direct
c) La droite (JQ) est la médiatrice du segment [PR] parce que le triangle PQR est équilatéral.
Donc, puisque J est le milieu de [QQ1], l'image PQ1R du triangle équilatéral direct PQR par la symétrie orthogonale d'axe (PR) est un triangle équilatéral indirect.
r est la rotation de centre P et d'angle (→PQ, →PR)=π3. Donc r(R)=Q1.
Ensuite, f(R)=t∘r(R)=t(Q1)=J ⇒ f(R)=J.
On sait que f=t∘r est une rotation de même angle que r c'est à dire π3.
La relation f(R)=J et JIR est équilatéral direct entraîne que le centre de f est I.
f est la rotation de centre I et d'angle π3.
On en déduit, puisque f(P)=P′ que le triangle IPP′ est équilatéral direct .
2) AntécédentΩJRIImage par sΩPIP′
a) L'angle de s est (→JR, →PI)=(→PJ, →PI). L'angle de s est −π6
Le rapport de s est PIJR. Or PI=PRcosπ6=2JR√32.
Donc le rapport de s est √3.
On a
(→RI, →IP′)=(→IQ, →IP′)=(→IQ, →IP)+(→IP, →IP′)=−π2+π3=−π6angle de s
IP′RI=IPRI=√3 rapport de s.
Les trois conditions :
{s(R)=I(→RI, →IP′)=angle de sIP′RI=rapport de ssuffisent pour dire que s(I)=P′
b) Puisque les similitudes planes directes conservent les angles, on peut lire dans le tableau précédent que : angle de s=(→ΩR, →ΩI)=(→JR, →PI).
Or (→JR, →PI)=(→PR, →PI) parce que le point J appartient au segment [PR].
Donc (→ΩR, →ΩI)=(→PR, →PI) et comme les quatre points Ω, R, P et I ne sont pas alignés, ils sont cocycliques.
De même −π6=angle de s=(→ΩJ, →ΩP).
D'un autre côté, la droite (Q1J) étant la bissectrice du triangle équilatéral indirect PQ1R, l'angle (→Q1J, →Q1P) vaut −π6
On en déduit que (→ΩJ, →ΩP)=(→Q1J, →Q1P) puis que les points Ω, J, P et Q1 sont cocycliques
En résumé, le point Ω appartient à l'intersection des deux cercles C1 et C2 ; où C1 est le cercle contenant les points P, I et R et C2 le cercle contenant les points P, J et Q1.
De plus le point Ω est différent de P parce que Ω est fixé par s et P non.
Ces conditions définissent parfaitement le point Ω.
Problème
1) a) Nous sommes en présence d'une équation différentielle linéaire homogène à coefficients constants de degré un ou deux selon que m est égal à 0 ou non.
L'équation caractéristique est : (Ecm) : mr2+2r+2=0
− Si m=0, (Ecm) est une équation du premier degré. Sa seule racine est r0=−1.
La solution générale de l'équation (Em) est alors y=ke−t, k constante réelle.
− Si m≠0, (Ecm) est une équation du second degré dont le discriminant réduit est Δ′=1−2m.
∗ Si Δ′ est égal à 0 c'est à dire m=12, l'équation (Ecm) a une racine double r0=−1m=−2.
La solution générale de l'équation (Em) est alors y=(at+b)e−2t, a et b constantes réelles.
∗ Si Δ′>0 c'est à dire m<12, l'équation (Ecm) a deux racines réelles simples
r1=−1+√1−2mmetr2=−1−√1−2mm
La solution générale de l'équation (Em) est alors y=aer1t+ber2t, a et b constantes réelles.
∗ Si Δ′<0 c'est à dire m>12, l'équation (Ecm) a deux racines complexes simples conjuguées
z1=−1+i√2m−1m=α+iβetz2=−1−i√2m−1m=α−iβ
avec α=−1m et β=√2m−1m
La solution générale de l'équation (Em) est alors y=eαt(acosβt+bsinβt), a et b constantes réelles.
b) Notons h la solution de (E1) dont la courbe passe par le point A et admet en ce point une tangente parallèle à la droite d'équation y=−x.
On doit alors avoir h(0)=1 et h′(0)=−1.
Ici m=1 est > à 12, donc h s'écrit : h(t)=e−t(acost+bsint), a et b constantes réelles.
h′(t)=[(b−a)cost−(b+a)sint]e−t
Les conditions satisfaites par h deviennent : h(0)=a=1 et h′(0)=b−a=−1 c'est à dire a=1 et b=0 puis h(t)=coste−t
2) La fonction f est continue et dérivable dans I=[−π2, 3π2] et ∀t∈I, f′(t)=−(cost−sint)e−t (déjà calculé dans la question précédente).
L'équation cost+sint=0 est équivalente à cos(t−π4)=0. Ses solutions dans R sont telles que
t−π4=π2+kπ, k∈Zsoit t=3π4+kπ, k∈Z
Les solutions de cette équation dans I sont alors t0=3π4 et t1=−π4.
Cette équation et la dérivée f′ ont les mêmes zéro.
Pour déterminer le signe de f′ on peut résoudre des inéquations trigonométriques.
Mais on peut aussi dire que dans tout intervalle où f′ ne s'annule pas, elle garde un signe constant parce qu'elle est continue. C'est une application très pratique du théorème des valeurs intermédiaires.
−π3 appartient à l'intervalle I1=[−π2, −π4] et f′(−π3)=(√32−12)eπ3 est > 0, donc f′ est > 0 dans I1.
0 appartient à l'intervalle I2=[−π4, 3π4] et f′(0)=−1 est < 0, donc f′ est < 0 dans I2.
π appartient à l'intervalle I3=[3π4, 3π2] et f′(π)=e−π est > 0, donc f′ est > 0 dans I3.
Voici le tableau de variations de f.
t−π2−π43π43π2f′+|−|+r0f↗↘↗0s
s=−√22e−3π4,r=√22eπ4
Et voici les courbes représentatives de f, u et v.
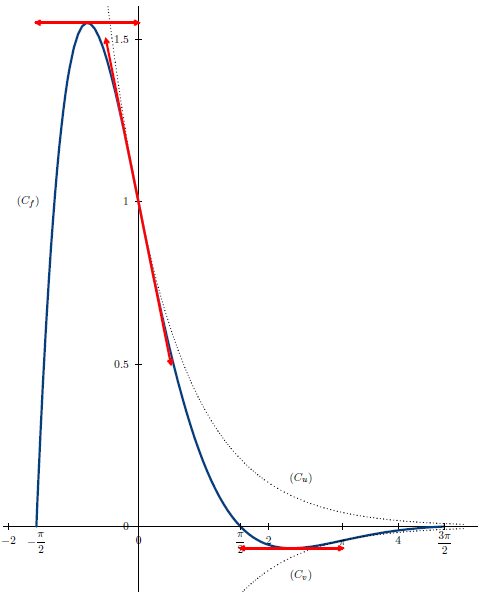
3) a) Pour tout k appartenant à Z et tout t appartenant à R, g(t+2kπ)=e−t−2kπcost parce que la fonction cosinus est périodique de période 2π.
Donc g(t+2kπ)=e−2kπg(t).
En dérivant cette dernière expression par rapport à t on obtient : g′(t+2kπ)=e−2kπg′(t).
En particulier pour tout t appartenant à I et tout k appartenant à Z, g′(t+2kπ)=e−2kπf′(t).
Cette relation permet de déterminer parfaitement le signe de g′ dans R.
Plus précisément :
Si t appartient à un intervalle du genre [−π2+2kπ, −π4+2kπ] ou [3π4+2kπ, 3π2+2kπ], k∈Z alors g′(t) est positif
Si t appartient à un intervalle du genre [−π4+2kπ, 3π4+2kπ], k∈Z alors g′(t) est positif
b) Un point M de coordonnées (t, u(t)) appartient à Γ∩Cu si et seulement si u(t)=g(t) c'est
à dire cost=1 ou t=2kπ, k appartenant à Z, et alors u(t)=e−2kπ.
Donc Γ∩Cu={M(2kπ, e−2kπ), k∈Z}
Un point M de coordonnées (t, v(t)) appartient à Γ∩Cv si et seulement si v(t)=g(t) c'est
à dire cost=−1 ou t=(2k+1)π, k appartenant à Z, et alors v(t)=e−(2k+1)π.
Donc Γ∩Cv={M((2k+1)π, e−(2k+1)π), k∈Z}
c) En un point M(2kπ, e−2kπ) commun à Γ et à Cu, la pente de la tangente à Γ est
g′(2kπ)=e−2kπg′(0)=e−2kπf′(0)=−e−2kπ
et la pente de la tangente à Cu est
u′(2kπ)=−e−t|t=2kπ=−e−2kπ
Les deux tangentes ayant même pente et passant par le point M sont confondues.
En un point M((2k+1)π, e−(2k+1)π) commun à Γ et à Cv, la pente de la tangente à Γ est
g′((2k+1)π)=e−2kπg′(π)=e−2kπf′(π)=−e−(2k+1)π
et la pente de la tangente à Cv est
v′((2k+1)π)=−e−t|t=(2k+1)π=−e−(2k+1)π
Les deux tangentes ayant même pente et passant par le point M sont confondues.
d) 0≤|coste−t|≤e−t. Or limt→+∞e−t=0
Le théorème des gendarmes permet de conclure que limt→+∞g(t)=0.
4) a) Pour simplifier posons rk=−π2+kπ, sk=π2+kπ de sorte que ak=∫skrkgk(t)dt
ensuite intégrons une première fois par parties en posant :
{u(t)=e−t⇒u′(t)=−e−tv′(t)=cost⇐v(t)=sint
Alors ak=[sinte−t]skrk+∫skrksinte−tdt
intégrons une deuxième fois par parties en posant :
{u(t)=e−t⇒u′(t)=−e−tv′(t)=sint⇐v(t)=−cost
Alors ak=[sinte−t]skrk+[−coste−t]skrk−∫skrkcoste−tdt
c'est à dire ak=[(sint−cost)e−t]skrk−ak ou ak=12[(sint−cost)e−t]skrk
Or cosrk=cossk=0 et sinrk=(−1)k+1 et sinsk=(−1)k
Donc
ak=12(−1)k[e−sk−(−1)k+1e−rk]=12(−1)k[e−sk+e−rk]=12(−1)ke−kπ[e−π2+eπ2]
b) sn=Ch∑nk=0e−kπ avec Ch=12[e−π2+eπ2]
La somme est la somme des n+1 premiers termes de la progression géométrique de premier terme 1 et de raison e−π
Donc sn=Ch.1.1−e−(n+1)π1−e−π
Puisque limn↦+∞e−(n+1)π=0, la suite (sn) admet une limite et cette limite est égale à : s=limn↦+∞sn=Ch11−e−π
sn représente l'aire géométrique du domaine plan délimité par l'axe des abscisses, la verticale d'équation x=−π2, la verticale d'équation x=π2+nπ et la courbe représentative de g.
s représente l'aire géométrique du domaine plan délimité par l'axe des abscisses, la verticale d'équation x=−π2 et la courbe représentative de g.
5) a) x′t=−(cost+sint)e−t et y′t=(cost−sint)e−t
On a :
x′t=−(cost+sint)e−t=−cos(t−π4)√2e−t=cos(π+t−π4)√2e−t=cos(t+3π4)√2e−t
et
y′t=(cost−sint)e−t=−sin(t−π4)√2e−t=sin(π+t−π4)√2e−t=sin(t+3π4)√2e−t
Les zéro de x′ sont t1=−π4 et t2=3π4
Le zéro de y′ est t3=π4
On détermine les signes de x′ et y′ par la méthode utilisée pour déterminer le signe de f′.
Voici le tableau de variations conjointes.
t−π2−π4π43π43π2x′+|−|−|+r||0x↗|↘s↘|↗0||t|s|y↗−r↗|↘−t↘v|||uy′+|+|−|−
r=√22eπ4,s=√22e−π4,t=−√22e−3π4,u=−e−3π2,v=−eπ2
Voici la courbe (Λ)
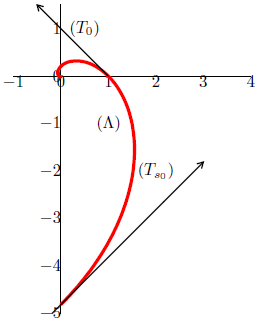
La tangente (Ts0) au point de paramètre s0=−π2 est la droite passant par le point de coordonnées (0, −e−s0) et dont un vecteur directeur a pour coordonnées (x′s0, y′s0)=(e−s0, e−s0) ou (1, 1).
La tangente (T0) au point de paramètre 0 est la droite passant par le point de coordonnées (1, 0)
et dont un vecteur directeur a pour coordonnées (x′s0, y′s0)=(−1, 1).
b) Rappelons que θ étant un réel, le plan étant muni d'un repère orthonormé (O; →i, →j) et en désignant par Mθ le point de cordonnées (λcosθ, λsinθ), λ>0 alors θ est une mesure de l'angle (→i, →OMθ).
On en déduit que (→i, →OMt)≡t
→Vt a pour coordonnées x′t=cos(t+3π4)√2e−t et y′t=sin(t+3π4)√2e−t
Donc (→i, →Vt)≡t+3π4.
Puis (→OMt, →Vt)=(→OMt, →i)+(→i, →Vt)≡3π4.
Auteur: Mouhamadou Ka

Ajouter un commentaire