Corrigé Bac Maths S2 1er groupe 2016
Exercice 1
1. a. Soit α une solution réelle de (E) alors α vérifie α3−13α2+59α−87=0.
Une solution évidente est 3.
D'où α=3
1. b. (z−3)(z2−10z+29)=0.
D'où z=3 ou z2−10z+29=0.
Après calculs z=3 ou z=5−2i ou z=5+2i.
L'ensemble des solutions est : S={3; 5−2i; 5+2i}.
2. a b−ac−a=−i.
{arg(b−ac−a)≡−π2⇔(→AC, →AB)≡−π2[2π]AB=AC
ABC est rectangle et isocèle en A et direct.
2. b. ArgZ≡(→MB, →MA) [2π].
Z réel non nul si et seulement si argZ≡0 (π).
(→MB, →MA) (π).
M décrit la droite (AB) privée de A et de B.
3. a. Soit M′(Z′) l'image de M(Z) par la rotation r de centre I et d'angle −π2
Donc Z′−Zi=e−π2(Z−Zi).
On obtient Z′=−iZ+3+i
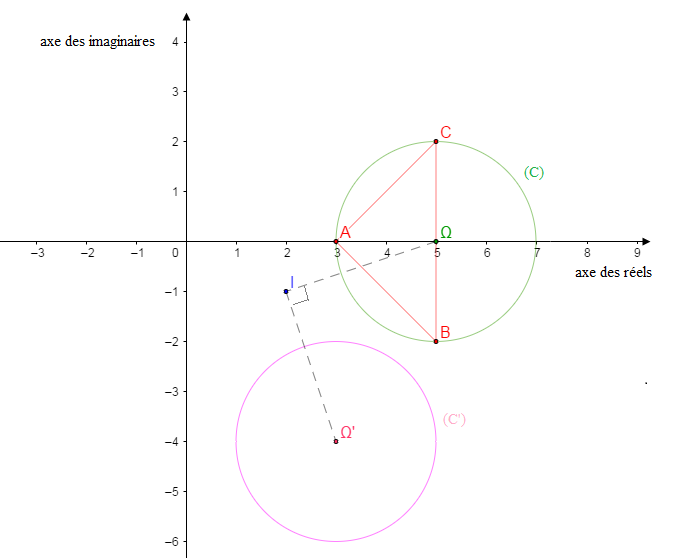
3. b. Soit Ω centre du cercle circonscrit à ABC.
Ω est le milieu de [BC].
On a ZΩ=ZB+ZC2
ce qui donne ZΩ=5.
Soit r(Ω)=Ω′, ZΩ′=−iZΩ+3+i. D'où ZΩ′=3−4i.
Donc (C′) est le cercle de centre Ω′ et de même rayon que (C).
Exercice 2
1. p(A)=C24C25p(A)=35.
p(B)=C14×C11C25p(B)=25.
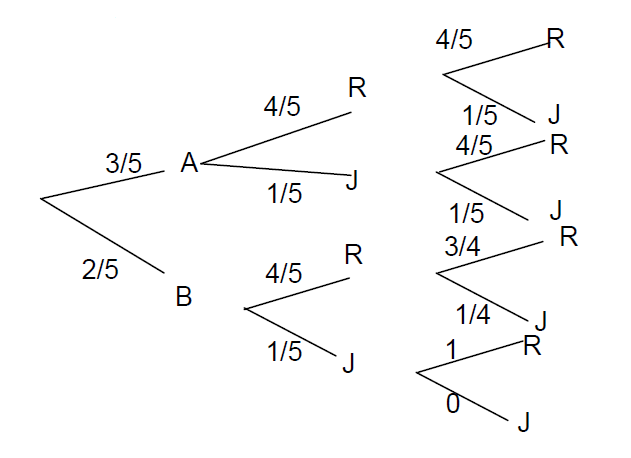
p(C)=45×45+15×15p(C)=1725.
p(D)=45×34p(D)=35.
p(E)=45×14+15×1p(E)=25.
p(F)=25×45×14+25×15×1p(F)=425.
2.a. X(Ω)={(R, R), (R, J), (J, R), (J, J)} Les différentes valeurs prises par X sont 0; 1000 et 2000.
a010002000P(X=a)31254412578125
b. Fonction de répartition
− si x<0, F(x)=0.
− si 0≤x<1000, F(x)=3125
− si 1000≤x<2000, on a F(x)=3125+44125.
D'où si 1000≤x<2000, F(x)=47125
− si x≥2000 F(x)=35+44125+78125=1
3. p(G)=(78125)50p(H)=(3125)50p(I)=(44125)50+C2550(3125)25(78125)25
Problème
Partie A
1. a. g(x) existe si et seulement si: {x+1>0x+1≠0
ce que donne x>−1.
Dg=]−1, +∞[.
limx→−1+−2(x+1)ln(x+1)+x(x+1),
limx→−1+g(x)=−∞ par quotient
limx→+∞g(x)=−∞ car {−2ln(x+1)→−∞ par composée puis produit xx+1→1
1. b. g′(x)=−2x+1+(xx+1)′g′(x)=−2x−1(x+1)2
x−1−12+∞g′(x)+0−
Tableau de Variation
x−1−12+∞g′(x)+0−g↗2ln2−1↘−∞−∞
2. a. g(0)=0.
La restriction de g à ]−1; −12 est strictement croissante et continue et prend ses valeurs dans ]−∞, 2ln2−1[ qui contient donc l'équation g(x)=0 admet sur ]−1; −12
une solution unique α.
Idem sur ]−12; +∞[, l'équation g(x)=0 admet un solution unique 0 .
]−0.72; −0.71[⊂]−1; −12[
et g(−0.72)×g(−0.71)<0 donc α∈]−0.72; −0.71[.
2. b. 0 étant l'autre zéro de g :
x−1α0+∞g(x)−0+0−
Partie B
1. a. Domaine de définition de f.
f(x) existe si et seulement si: {x+1>0ln(x+1)≠0
- ou x∈]−∞, −1],
- ou x=0
d'où {x>−1x≠0 ou x∈]−∞, −1] ou x=0
Df=(]−1, +∞∖{0})∪]−∞, −1]∪{0}
Df=R
Limites aux bornes du domaine de définition de f.
limx→−∞f(x)=−∞; limx→+∞f(x)=limx→+∞x2x+1×(x+1)ln(x+1)=+∞,
limx→+∞f(x)=+∞
1.b. Étudions la nature de la branche infinie au voisinage de −∞ .
limx→−∞f(x)x=limx→−∞(x+1x)e−x−1=+∞
limx→−∞f(x)x=+∞
Donc (Cf) admet au voisinage de −∞ une branche parabolique de direction celle de l'axe des ordonnées
Étudions la nature de la branche infinie au voisinage de +∞.
limx→+∞f(x)x=limx→+∞(xx+1)(x+1)ln(x+1)=+∞
Donc (Cf) admet au voisinage de −∞ une branche parabolique de direction celle de l'axe des ordonnées
2. a.
f(−1)=0.
limx→−1+f(x)=0 par quotient et limx→−1−f(x)=f(−1)=0
D'où limx→−1+f(x)=limx→−1−f(x)=f(−1)=0
Donc est continue en -1.
On a f(0)=0
limx→0f(x)=limx→0x×xln(x+1)=0
D'où limx→0f(x)=f(0)
Donc est continue en 0.
2. b. Dérivabilité de f en -1.
limx→−1−f(x)−f(−1)x+1=limx→−1(x+1)(x+1)e−x−1=1
f dérivable en -1 à gauche et f′g(−1)=1
limx→−1+f(x)−f(−1)x+1=limx→−1+x2(x+1)ln(x+1)=−∞
Donc non dérivable en -1 car non dérivable en -1 à droite.
Interprétation point d'abscisse -1.
Au point d'abscisse -1 (Cf) admet une demi-tangente verticale et une demi- tangente de pente 1 à gauche.
Dérivabilité de f en 0.
limx→0f(x)−f(0)x−0=limx→0xln(x+1)=1
Donc est dérivable en 0 et f′(0)=1.
Interprétation au point d'abscisse 0.
(Cf) admet à l'origine une tangente de coefficient directeur 1.
3. a. Pour tout x∈]−1, +∞[∖{0} on a f′(x)=(x2ln(x+1))′=2xln(x+1)−x2x+1(ln(x+1))2=−x(−2ln(x+1)+xx+1)(ln(x+1))2
f′(x)=−xg(x)(ln(x+1))2
Pour x<−1, f′(x)=−xe−x−1
3. b.
x−∞−1α0+∞f′(x)+||−0+f00+∞↗↘↗−∞f(α)
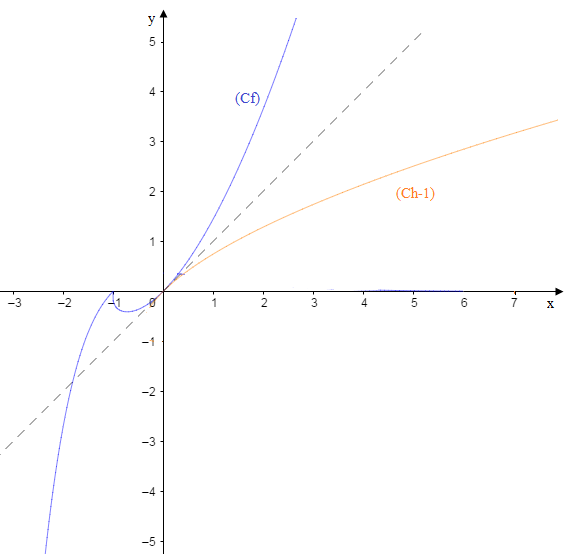
4. a h est continue et strictement croissante sur [0, +∞[, elle réalise donc une bijection de [0, +∞[ vers [0, +∞[=J
4. b. h−1 a le même sens de variation que , elle est strictement croissante sur J.
4. c. Figure :
Partie C
1. a. Posons u′(x)=1x2 et v′(x)=1x+1 avec u(x)=−1x et v(x)=ln(x+1).
Sur ]0, +∞[, on a m(x)=1x2ln(x+1)+(−1x)(1x+1).(R)
1. b. On a m(x)=(u(x)v(x))′.
Pour tout x∈]0, +∞[ on a H′(x)=m(x) avec m(x)=(u(x)v(x))′.
D'où on a : H(x)=u(x)v(x)+c=−ln(x+1)x+c.
On a sur x∈]0, +∞[, 1f(x)=ln(x+1)x2 on ’ m e m ’
Or d'après (R) : ln(x+1)x2=m(x)+1x×1x+1=m(x)+1x−1x+1.
Soit G une primitive de la fonction x→ln(x+1)x2.
∫211f(x)dx=[G(x)]21=[H(x)+ln(xx+1)]21=[−ln(x+1)x+c+ln(xx+1)]21=−3ln22+3ln2
∫211f(x)dx=3(ln2−ln√3)=3ln(2√33)
Source: Office du Bac Sénégal

Ajouter un commentaire