Vous êtes ici

Corrigé BFEM Maths 2018

Exercice 1

1) Recopions et complétons chacune des phrases ci-dessous.

1-1) Soit

$a\$ et

$\ b$ deux réels tels que

$b$ soit positif,

$\sqrt{ba^{2}}=|a|\sqrt{b}$

1-2) L'équation

$x\sqrt{8}-8=0$ a pour solution

$x=2\sqrt{2}$

1-3)

$m\;,\ n\$ et

$\ q$ sont des entiers naturels.

Une expression conjuguée de

$-m+q\sqrt{n}$ est

$-m-q\sqrt{n}$

2) Soit les nombres réels suivants :

$a=5-2\sqrt{6}\quad b=5+2\sqrt{6}\quad\text{et}\quad c=-5+2\sqrt{6}$

2-1) Montrons que

$a\$ et

$\ b$ sont inverses.

On a :

$a$ et

$b$ sont inverses si, et seulement si,

$a\times b=1$

Donc, calculons le produit

$a\times b$

On a :

$\begin{array}{rcl} a\times b&=&(5-2\sqrt{6})(5+2\sqrt{6})\\\\&=&(5)^{2}-(2\sqrt{6})^{2}\\\\&=&25-4\times 6\\\\&=&25-24\\\\&=&1\end{array}$

Ainsi,

$a\times b=1$ , d'où

$a\$ et

$\ b$ sont inverses.

2-2) Montrons que

$a\$ et

$\ c$ sont opposés.

$a\$ et

$\ b$ sont opposés si, et seulement si,

$c=-a$ ou encore

$a+c=0.$

On a :

$c=-5+2\sqrt{6}=-(5-2\sqrt{6})$

donc, on voit bien que

$c=-a$

Ce qui montre alors que

$a\$ et

$\ c$ sont opposés.

$MARE$ est un carré de coté

$MA=5+2\sqrt{6}.$

Déterminons la valeur exacte de sa diagonale.

$MARE$ étant un carré alors,

$MAR$ est un triangle rectangle en

$A.$

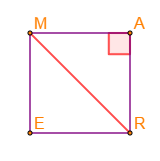
Donc, sa diagonale

$MR$ représente l'hypoténuse du carré

$MAR.$

Ainsi, d'après le théorème de Pythagore on aura :

$MR^{2}=MA^{2}+AR^{2}=2MA^{2}$

par suite :

$\begin{array}{rcl} MR&=&\sqrt{2\times MA^{2}}\\\\&=&\sqrt{2\times(5+2\sqrt{6})^{2}}\\\\&=&\sqrt{2}\times|5+2\sqrt{6}|\\\\&=&\sqrt{2}\times(5+2\sqrt{6})\\\\&=&5\sqrt{2}+2\sqrt{12}\\\\&=&5\sqrt{2}+4\sqrt{3}\end{array}$

D'où,

$\boxed{MR=5\sqrt{2}+4\sqrt{3}}$

Exercice 2

On considère la liste des notes obtenues par les élèves d'une classe de troisième, lors d'un devoir de mathématiques.

$\begin{array}{cccccccccc} 5&8&7&8&9&6&10&11&15&13 \\ 10&18&16&15&12&9&14&16&17&15 \\ 10&16&17&8&9&10&16&9&10&7 \\ 10&6&12&13&11&13&18&10&11&6 \\ 10&13&17&12&11&12&9&16&17&14\end{array}$

1) Regroupons ces notes par classes d'amplitude 3.

L'amplitude des classes étant égale à 3 alors, nous obtenons les classes suivantes :

$[5\;;\ 8[\;,\ [8\;;\ 11[\;,\ [11\;;\ 14[\;,\ [14\;;\ 17[\$ et

$\ [17\;;\ 20[$

2) Calculons la note moyenne.

Soit le tableau de notes suivants :

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline\text{Notes}&5&6&7&8&9&10&11&12&13&14&15&16&17&18\\ \hline\text{Effectifs}&1&3&2&3&5&8&4&4&4&2&3&5&4&2 \\ \hline\hline\text{"Produits"}&5&18&14&24&45&80&44&48&52&28&45&80&68&36 \\ \hline\end{array}$

Nous calculons d'abord les "Produits" partiels pour chaque note.

On a :

$\text{"Produit"}=\text{effectif partiel}\times\text{note}$

La note moyenne sera alors donnée par :

$M=\dfrac{\text{total des "Produits"}}{\text{effectif total}}$

ainsi, d'après les données du tableau ci-dessus on aura :

$\begin{array}{rcl} M&=&\dfrac{5+18+14+24+45+80+44+48+52+28+45+80+68+36}{50}\\\\&=&\dfrac{587}{50}\\\\&=&11.74\end{array}$

D'où,

$\boxed{\text{Note moyenne}=11.74}$

3) Calculons l'effectif cumulé croissant de chaque classe.

Pour cela, nous dressons le tableau suivant :

$\begin{array}{|c|c|c|c|c|c|}\hline\text{Classes de notes}&[5\;;\ 8[&[8\;;\ 11[&[11\;;\ 14[&[14\;;\ 17[&[17\;;\ 20[\\ \hline\text{Effectifs}&6&16&12&10&6 \\ \hline\hline\text{E.C.C}&6&22&34&44&50 \\ \hline\end{array}$

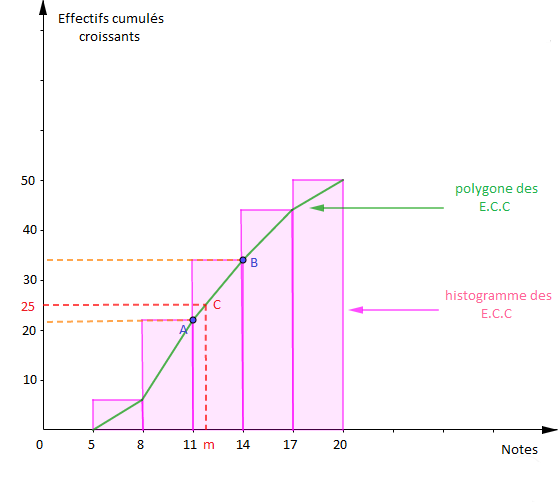
4) Traçons le diagramme des effectifs cumulés croissants.

$\text{Diagramme des effectifs cumulées croissants}$

5) Déterminons graphiquement la médiane de cette série.

La moitié de l'effectif total est

$\dfrac{50}{2}=25.$

Soit alors le point

$C$ d'ordonnée 25.

L'abscisse

$m$ du point

$C$ est appelée médiane de la série.

Calculons

$m.$

D'après le graphique, on voit bien que

$m$ appartient à la classe

$[11\;;\ 14[.$

De plus,

$A\;,\ C\;,\ B$ sont trois points alignés car

$C\in[AB]$ , donc les points

$A\;,\ C\$ et

$\ B$ appartiennent à la même droite.

Par ailleurs, les droites

$(AB)\$ et

$(AC)$ étant confondues donc, elles ont le même coefficient directeur.

Or, les coefficients directeurs de

$(AB)\$ et

$\ (AC)$ sont donnés respectivement par

$\dfrac{y_{B}-y_{A}}{x_{B}-x_{A}}\$ et

$\ \dfrac{y_{C}-y_{A}}{x_{C}-x_{A}}$

Donc on aura :

$\dfrac{y_{B}-y_{A}}{x_{B}-x_{A}}=\dfrac{y_{C}-y_{A}}{x_{C}-x_{A}}$

Ainsi,

$\dfrac{34-22}{14-11}=\dfrac{25-22}{m-11}\$ par suite,

$\dfrac{12}{3}=\dfrac{3}{m-11}$

Ce qui donne :

$12(m-11)=9\$ soit alors,

$m-11=\dfrac{9}{12}=\dfrac{3}{4}$

En résolvant cette équation on obtient alors :

$\begin{array}{rcl} m&=&\dfrac{3}{4}+11\\\\&=&\dfrac{3+44}{4}\\ \\&=&\dfrac{47}{4}\\ \\&=&11.75\end{array}$

D'où,

$\boxed{m=11.75}$

Autre méthode

$C\in[AB]$ alors, les points

$A\;,\ C\$ et

$\ B$ sont alignés.

Donc, les vecteurs

$\overrightarrow{AB}\begin{pmatrix} 14-11\\34-22\end{pmatrix}\$ et

$\ \overrightarrow{AC}\begin{pmatrix} m-11\\25-22\end{pmatrix}\$ sont colinéaires.

On a :

$\overrightarrow{AB}\begin{pmatrix} 3\\12\end{pmatrix}\$ et

$\ \overrightarrow{AC}\begin{pmatrix} m-11\\3\end{pmatrix}$ colinéaires si, et seulement si,

$3\times 3-12\times(m-11)=0$

Soit alors,

$9-12m+132=0$

Ce qui donne :

$12m=141$

et par suite,

$m=\dfrac{141}{12}=\dfrac{47}{4}$

Ainsi,

$\boxed{m=11.75}$

Exercice 3

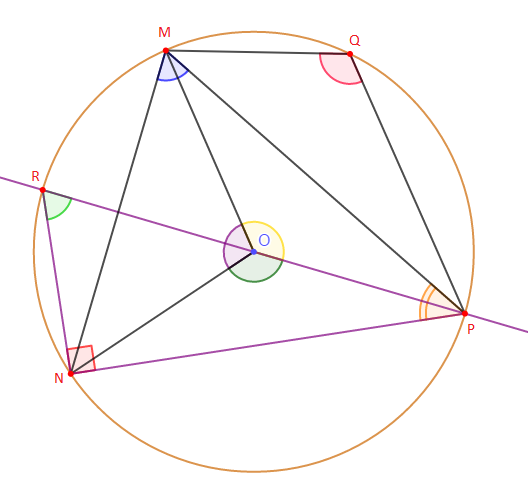
Soit un cercle de centre

$O$ et de rayon

$4\;cm.$

$M\;,\ N\$ et

$\ P$ sont trois points de ce cercle tels que :

$\widehat{NOP}=130^{\circ}\;,\quad\widehat{MPN}=50^{\circ}$ et la bissectrice de

$\widehat{MPN}$ passe par

$O.$

1) Faisons la figure

2) Déterminons les mesures des angles

$\widehat{MON}\;,\ \widehat{NMP}\$ et

$\ \widehat{MOP}$

$\centerdot\ mes\;\widehat{MON}$

On a :

$\widehat{MPN}$ un angle inscrit dans

$(C)$ ayant pour angle au centre associé

$\widehat{MON}$

donc,

$\ \widehat{MON}=2\widehat{MPN}$

puisque

$\ \widehat{MPN}=50^{\circ}$ alors,

$\ \widehat{MON}=2\times 50=100^{\circ}$

d'où,

$\boxed{mes\;\widehat{MON}=100^{\circ}}$

$\centerdot\ mes\;\widehat{NMP}$

On a :

$\widehat{NMP}$ un angle inscrit dans

$(C)$ ayant pour angle au centre associé

$\widehat{NOP}$

donc,

$\ 2\widehat{NMP}=\widehat{NOP}$

et comme

$\ \widehat{NOP}=130^{\circ}$ alors,

$\ 2\widehat{NMP}=130^{\circ}$

par suite,

$\ \widehat{NMP}=\dfrac{130}{2}=65^{\circ}$

par conséquent,

$\boxed{mes\;\widehat{NMP}=65^{\circ}}$

$\centerdot\ mes\;\widehat{MOP}$

On a :

$\widehat{MNP}$ un angle inscrit dans

$(C)$ ayant pour angle au centre associé

$\widehat{MOP}$

donc,

$\ \widehat{MOP}=2\widehat{MNP}$

mais on sait que dans un triangle, la somme des angles est égale à

$180^{\circ}$

donc, pour le triangle

$MNP$ on aura :

$\widehat{MNP}+\widehat{NMP}+\widehat{MPN}=180^{\circ}$

De cette relation, on en déduit alors la mesure de l'angle

$\widehat{MNP}.$

Ainsi :

$\begin{array}{rcl} \widehat{MNP}&=&180-\widehat{NMP}-\widehat{MPN}\\\\&=&180-65-50\\\\&=&180-115\\\\&=&65 \end{array}$

D'où,

$mes\;\widehat{MNP}=65^{\circ}$

Comme on avait

$\widehat{MOP}=2\widehat{MNP}$ et que

$mes\;\widehat{MNP}=65^{\circ}$ alors,

$\widehat{MOP}=2\times 65=130.$

Par conséquent,

$\boxed{mes\;\widehat{MOP}=130^{\circ}}$

Remarque :

On a :

$mes\;\widehat{MNP}=mes\;\widehat{NMP}=65^{\circ}$ donc, le triangle

$MNP$ est isocèle en

$P.$

3) Soit

$Q$ un point de l'arc

$\overset{\displaystyle\frown}{MP}$ distinct de

$P\$ et

$\ M.$

Montrons que les angles

$\widehat{NMP}\$ et

$\ \widehat{MQP}$ sont supplémentaires.

$MNPQ$ étant un quadrilatère convexe inscriptible dans le cercle

$(C)$ alors, les angles opposés sont supplémentaires.

Donc,

$\widehat{MNP}\$ et

$\ \widehat{MQP}$ sont supplémentaires.

Ce qui revient à dire :

$\widehat{MNP}+\widehat{MQP}=180^{\circ}$

Or, d'après la remarque de la question 2)

$\widehat{MNP}=\widehat{NMP}$ car

$MNP$ est isocèle en

$P.$

Ainsi,

$\begin{array}{rcl} \widehat{NMP}+\widehat{MQP}&=&\widehat{MNP}+\widehat{MQP}\\\\&=&180\end{array}$

d'où,

$\boxed{\widehat{NMP}+\widehat{MQP}=180^{\circ}}$

Ce qui montre que les angles

$\widehat{NMP}\$ et

$\ \widehat{MQP}$ sont supplémentaires.

4) La bissectrice de l'angle

$\widehat{MPN}$ recoupe le cercle au point

$R.$

Déterminons les mesures des angles du triangle

$NRP.$

$NRP$ est un triangle inscrit dans

$(C)$ et on sait que la bissectrice de l'angle

$\widehat{MPN}$ passe par

$O$ et recoupe le cercle au point

$R.$

Donc,

$[RP]$ est un diamètre de

$(C).$

D'où,

$NRP$ est rectangle en

$N$

Par suite :

$\boxed{mes\;\widehat{RNP}=90^{\circ}}$

La droite

$(RP)$ étant bissectrice de l'angle

$\widehat{MPN}$ alors,

$\begin{array}{rcl}\widehat{RPN}&=&\dfrac{\widehat{MPN}}{2}\\ \\&=&\dfrac{50}{2}\\ \\&=&25\end{array}$

Ainsi,

$\boxed{mes\;\widehat{RPN}=25^{\circ}}$

Enfin, on sait que dans un triangle rectangle les angles aigus sont complémentaires.

Donc :

$\widehat{NRP}+\widehat{RPN}=90^{\circ}$

Comme

$\widehat{RPN}=25^{\circ}$ alors,

$\begin{array}{rcl} \widehat{NRP}&=&90-\widehat{RPN}\\\\&=&90-25\\\\&=&65\end{array}$

D'où,

$\boxed{mes\;\widehat{NRP}=65^{\circ}}$

Autre méthode

$\widehat{NRP}$ un angle inscrit dans

$(C)$ ayant pour angle au centre associé

$\widehat{NOP}$

donc,

$\ 2\widehat{NRP}=\widehat{NOP}$

et comme

$\ \widehat{NOP}=130^{\circ}$ alors,

$\ 2\widehat{NRP}=130^{\circ}$

par suite,

$\ \widehat{NRP}=\dfrac{130}{2}=65^{\circ}$

D'où,

$\boxed{mes\;\widehat{NRP}=65^{\circ}}$

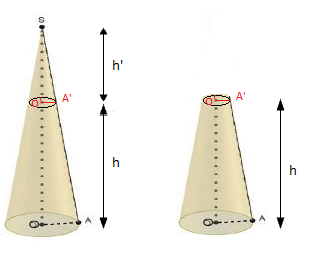
Exercice 4

La figure ci-dessous représente une bougie qui a la forme d'un cone de révolution de rayon de base

$OA=22.5\;cm$ et de génératrice

$AS=37.5\;cm$

1) Montrons que la hauteur

$OS$ de la bougie est de

$30\;cm$

On sait que

$AOS$ est un triangle rectangle en

$O$ donc, d'après le théorème de Pythagore on a :

$OS^{2}+OA^{2}=AS^{2}$

par suite :

$OS^{2}=AS^{2}-OA^{2}$

d'où :

$\begin{array}{rcl} OS&=&\sqrt{AS^{2}-OA^{2}}\\\\&=&\sqrt{(37.5)^{2}-(22.5)^{2}}\\\\&=&\sqrt{1406.25-506.25}\\\\&=&\sqrt{900}\\\\&=&30\end{array}$

Ainsi, on a bien

$\boxed{OS=30\;cm}$

2) Calculons le volume de cire nécessaire à sa confection.

Pour calculer le volume

$\mathcal{V}$ de cire nécessaire à sa confection, on calcule tout simplement le volume de ce cône.

Comme

$\mathcal{V}_{\text{cône}}=\dfrac{1}{3}\times\pi\times(\text{Rayon de base})^{2}\times(\text{Hauteur})$

alors,

$\begin{array}{rcl} \mathcal{V}&=&\dfrac{1}{3}\times\pi\times OA^{2}\times OS\\ \\&=&\dfrac{1}{3}\times\pi\times(22.5)^{2}\times(30)\\ \\&=&\dfrac{3.14\times 506.25\times 30}{3}\\ \\&=&15896.25\end{array}$

D'où, le volume de cire nécessaire à la confection de cette bougie est :

$\boxed{\mathcal{V}=15896.25\;cm^{3}}$

3) Calculons l'aire

$\mathcal{A}$ de la surface minimale de papier nécessaire pour l'envelopper entièrement.

Pour cela, on calcule l'aire latérale

$\mathcal{A}_{L}$ du cône.

Or,

$\mathcal{A}_{L}=\pi\times(\text{Rayon de base})\times(\text{Génératrice})$

Donc,

$\begin{array}{rcl} \mathcal{A}_{L}&=&\pi\times OA\times AS\\\\&=&3.14\times 22.5\times 37.5\\\\&=&2649.375\end{array}$

Ainsi, l'aire de la surface minimale de papier nécessaire pour l'envelopper entièrement est :

$\boxed{\mathcal{A}=2649.375\;cm^{2}}$

4) Déterminons le temps

$t$ nécessaire pour que la bougie soit entièrement consumée.

On sait que chaque minute, la bougie se consume en diminuant de

$101.25\;cm^{3}$ de son volume.

Donc,

$\begin{array}{rcl} t&=&\dfrac{\mathcal{V}}{101.25}\\\\&=&\dfrac{15896.25}{101.25}\\\\&=&157\end{array}$

Ce qui donne alors,

$t=157\;mn$ soit ; 2 heures et 37 minutes.

Ainsi, au bout de 2 heures 37 minutes, la bougie sera entièrement consumée.

5) Soit

$k$ le coefficient de réduction du cone réduit représentant la partie consumée de la bougie,

$\mathcal{V}$ le volume du cone initial qui représente la bougie et

$\mathcal{V}'$ le volume de la partie restante de la bougie.

5)1) Montrons que

$\mathcal{V}'=(1-k^{3})\mathcal{V}$

Appelons

$\mathcal{V}''$ le volume du cône réduit représentant la partie consumée.

Comme nous sommes dans le cas d'une réduction avec

$k$ coefficient de réduction alors,

$\mathcal{V}''=k^{3}\times\mathcal{V}.$

Ainsi,

$\begin{array}{rcl} \mathcal{V}'&=&\mathcal{V}-\mathcal{V}''\\\\&=&\mathcal{V}-k^{3}\mathcal{V}\\\\&=&\mathcal{V}(1-k^{3})\end{array}$

Ce qui montre que

$\boxed{\mathcal{V}'=(1-k^{3})\mathcal{V}}$

5)2) Montrons que

$k=\dfrac{30-h}{30}$

On a :

$k=\dfrac{O'S}{OS}\$ or,

$O'S=OS-h$

donc,

$k=\dfrac{OS-h}{OS}\$ avec

$OS=30\;cm$

Par conséquent,

$\boxed{k=\dfrac{30-h}{30}}$

5)3) Calculons la hauteur de la partie restante de la bougie au bout d'une heure d'éclairage.

Soit

$h$ la hauteur de la partie restante de la bougie au bout d'une heure d'éclairage.

D'après question 5)2) on a :

$k=\dfrac{30-h}{30}.$

Donc,

$30k=30-h$ soit ;

$h=30-30k$

Ce qui peut s'écrire encore

$h=30(1-k)$

Donc, pour trouver

$h$ essayons de déterminer

$k.$

Pour cela, trouvons d'abord les volumes de la partie de bougie consumée et restante.

Au bout d'une heure d'éclairage, le volume

$\mathcal{V}''$ du cône réduit représentant la partie consumée est donnée par :

$\mathcal{V}''=101.25\times t$

Or,

$t=1\;h=60\;mn$ donc,

$\begin{array}{rcl} \mathcal{V}''&=&101.25\times t\\\\&=&101.25\times 60\\\\&=&6075\end{array}$

d'où,

$\boxed{\mathcal{V}''=6075\;cm^{3}}$

Par suite, le volume

$\mathcal{V}'$ de la partie restante de la bougie est :

$\begin{array}{rcl} \mathcal{V}'&=&\mathcal{V}-\mathcal{V}''\\\\&=&15896.25-6075\\\\&=&9821.25\end{array}$

Ainsi,

$\boxed{\mathcal{V}'=9821.25\;cm^{3}}$

D'après question 5)1) on a :

$\mathcal{V}'=(1-k^{3})\mathcal{V}$

Donc,

$\dfrac{\mathcal{V}'}{\mathcal{V}}=1-k^{3}$

On peut alors en déduire que :

$\begin{array}{rcl} k^{3}&=&1-\dfrac{\mathcal{V}'}{\mathcal{V}}\\\\&=&1-\dfrac{9821.25}{15896.25}\\\\&=&1-0.6\\\\&=&0.4\end{array}$

Ainsi,

$k^{3}=0.4$

Or, d'après les données on a :

$(0.7)^{3}=0.4$

Ce qui permet de conclure que

$k=0.7$

Par conséquent, en remplaçant cette valeur de

$k$ dans l'expression de

$h$ on aura :

$\begin{array}{rcl} h&=&30(1-0.7)\\\\&=&30\times 0.3\\\\&=&9\end{array}$

Ainsi, la hauteur de la partie restante de la bougie au bout d'une heure d'éclairage est de

$9\;cm.$

Auteur:

Diny Faye

Commentaires

Anonyme (non vérifié)

mar, 09/01/2020 - 19:45

Permalien

Content d'avoir cette cette

Content d'avoir cette cette correction pour puisse aider nos frère

répondre

Anonyme (non vérifié)

mar, 09/01/2020 - 19:45

Permalien

Content d'avoir cette cette

Content d'avoir cette cette correction pour puisse aider nos frère

répondre

Anonyme (non vérifié)

mar, 05/18/2021 - 13:24

Permalien

Bien fait

répondre

Anonyme (non vérifié)

mer, 05/03/2023 - 01:38

Permalien

Je suis en classe de befem et

Je suis en classe de befem et je les besson

répondre

Anonyme (non vérifié)

dim, 07/09/2023 - 20:01

Permalien

Merci pour votre aide

répondre

Awa Gueye Basse (non vérifié)

mer, 07/17/2024 - 18:40

Permalien

Vraiment merci au fond cœur

Vraiment merci au fond cœur ces corrections nous sont très utiles

répondre

Anonyme (non vérifié)

dim, 05/18/2025 - 19:40

Permalien

n

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Corrigé BFEM Maths 2018

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Commentaires

Content d'avoir cette cette

Content d'avoir cette cette

Bien fait

Je suis en classe de befem et

Merci pour votre aide

Vraiment merci au fond cœur

n

Ajouter un commentaire

Plain text