1. Généralité sur les fonctions

1.1.  Définitions

$\mathbb{R}$ est l’ensemble des nombres réels. C’est un ensemble à la fois ouvert et fermé

$\mathbb{R}^*$ est l’ensemble des réels non nuls.  $\mathbb{R}$= ]−∞, 0[ ∪ ]0,+∞[ est un ouvert

$\mathbb{R}_+$ est l’ensemble des réels positifs ou nuls. $\mathbb{R}_+$ = [0,+∞[ est un ensemble fermé

$\mathbb{R}_{+}^{*}$ est l’ensemble des réels strictement positifs. $\mathbb{R}_{+}^{*}$ est un ouvert.

$\mathbb{R}_{-}$ est l’ensemble des réels négatifs ou nuls. $\mathbb{R}_{-}$ est un fermé.

$\mathbb{R}_{-}^{*}$ est l’ensemble des réels strictement négatifs. $\mathbb{R}_{-}^{*}$ est un  ouvert.

Comment savoir si un intervalle I est ouvert ou fermé ?

• Si I = ]a, b[ = {x tel que a < x < b}, avec a et b finis Alors I est ouvert
• Si I = [a, b] = {x tel que a ≤ x ≤ b}. avec a et b finis, Alors I est fermé
• Si I = [a, b[ = {x tel que a ≤ x < b}. avec a et b finis, alors I n’est ni ouvert, ni fermé
• Si I = ]a, b] = {x tel que a < x ≤ b}. avec a et b finis, alors I n’est ni ouvert, ni fermé
• Si a = −∞ ou si b = +∞, on ne regarde que la borne finie.

Définition : On appelle fonction numérique d’une variable réelle une application d’une partie $E \subset \mathbb{R}$  à valeurs dans $ \mathbb{R}$  . On note

$ f : E \to \mathbb{R} \\  x \mapsto f(x)$

Une fonction numérique n’est pas nécessairement définie pour tous les réels. Ainsi, la fonction

Exemples

En macroéconomie, on cherche souvent à représenter les comportements agrégés de consommation à l’aide d’une fonction de consommation. Celle-ci associe au revenu disponible des ménages Y d le niveau de consommation agrégée dans l’économie C. Modéliser les comportements de consommation à l’aide d’une telle fonction revient à considérer l’existence d’un lien systématique et automatique entre PIB et consommation agrégée. Cela revient également à négliger d’autres facteurs pouvant influencer la consommation agrégée. Il s’agit donc d’une hypothèse permettant une représentation commode mais très simplifiée de la réalité. Du point de vue mathématique, une telle fonction de consommation constitue une fonction numérique définie de $\mathbb{R}_+$ à valeurs dans $\mathbb{R}_+$

Les séries temporelles peuvent également être considérées comme des fonctions numériques pourvu que l’on adopte une représentation continue du temps. Ainsi la fonction qui à la date t ∈ R associe le PIB Yt à cette date constitue également une fonction numérique.

En microéconomie, on s’intéressera à la fonction de coût qui à un niveau de production y (par une unité de temps) associe le coût de production minimal

C (y) requis à la firme pour assurer cette production (sur cette unité de temps).

1.2. Domaine de définition

Définition : L’ensemble des réels pour lesquels la fonction f est définie s’appelle l’ensemble de définition de la fonction  . Il est noté $ D_f$ .

Remarque Les fonctions numériques sont, le plus souvent, définies par une expression mathématique, comme par exemple :

$f(x)=x^2+2x-5$           où    $f(x=\frac{3x+1}{2x-3}  $     .

Parfois, l’ensemble de définition est explicitement donné avec la définition de la fonction. Par exmple Soit  la fonction définie sur  .

Lorsque l’ensemble de définition n’est pas indiqué, il suffit d’examiner l’expression pour déterminer les conditions d’existence de f(x) :

• Y-a-t’il un dénominateur ? (celui-ci doit être non nul)
• Y-a-t’il une racine carrée ? (le radicande doit être positif ou nul)
• Y-a-t’il une fonction particulière non définie sur $\mathbb{R}$ (comme  ln par exemple).

Exemple : Donner le domaine de définition

$ f(x)=\frac{x+1}{x+1} \ \ \ g(x)=\sqrt{x-6} \ \ \ h(x)=x+3+\frac{1}{x}$

Définition : (fonction composée)

Soient f  et g deux fonctions numériques, on appelle fonction composée de g et de f et on note g ◦ f, la fonction g ◦ f (x) = g [f (x)]

Il ne faut pas confondre  g ◦ f (x) = g [f (x)] et  f ◦ g (x) = f [g (x)]

1.3.  Variation de fonction

Définition : Soit f une fonction numérique définie de E ⊂

• f  est croissante sur E ssi ∀x, y ∈ E tels que x < y, on ait f (x) ≤ f (y)
• f  est décroissante sur E ssi ∀x, y ∈ E tels que x < y, on ait f (x) ≥ f (y)
• f est strictement croissante sur E ssi ∀x, y ∈ E tels que x < y, on ait

f (x) < f (y)

• f  est strictement décroissante sur E ssi ∀x, y ∈ E tels que x < y, on ait

f (x) > f(y)

• f est monotone sur E ssi elle est croissante ou décroissante
• f est strictement monotone sur E ssi elle est strictement croissante ou décroissante.

1.4 Fonctions usuelles

2. Continuité d’une fonction

2.1. Notion de continuité

Définition : On considère une fonction f définie sur un intervalle I.

On dit que la fonction f est continue sur I si la courbe représentant la fonction f « se trace d’un trait continue ». (Sans lever le crayon)

Exemples :

• La fonction racine carrée est continue sur ]0,+∞[
• La fonction inverse est continue sur ]0,+∞[  mais n’est pas continue sur [-1 ; 1]

2.2. Fonctions usuelles

Propriétés :

• Les fonctions $x \mapsto x^n$ , où n est un entier naturel, sont continues sur $\mathbb{R}$
• Toute fonction polynôme est continue sur $\mathbb{R}$.
• Les fonctions $x \mapsto \frac{1}{x^n}$, où n est un entier naturel, sont continues sur    et sur .
• Toute fonction rationnelle est continue sur chaque intervalle de son ensemble de définition.

Exemples :

• La fonction f définie sur $\mathbb{R}$ par $f(x)=x^2-2x^3+x-7$ est continue sur $\mathbb{R}$.
• La fonction g définie par $g(x)=\frac{4x-1}{x-2}$  est continue sur $\mathbb{R}-\{ 2 \} $

Proposition: Si f et g sont continués en a alors, f + g, f − g, f · g, sont continués en a. Il en est de même de et si f (a) non nul ) et  (si g (a) non nul).

Pour les économistes, la notion de continuité sert à garantir l’existence de solutions à des  équations non linéaires. En effet, les théories économiques se formalisent souvent par des systèmes  de plusieurs équations à plusieurs inconnues (a priori il y a autant d’équations que d’inconnues).

Il est rare que ces systèmes soient linéaires, ce qui rend leur résolution explicite difficile voire  impossible. Or il existe néanmoins des outils mathématiques pour caractériser ces solutions. La première chose à caractériser est de savoir si une solution existe.

2.3. Théorème de la valeur intermédiaire

Définition : Une fonction est strictement monotone sur un intervalle I si elle est strictement croissante (ou strictement décroissante) sur cet intervalle.

Théorème (dit de la valeur intermédiaire) :

Si f est une fonction continue et strictement monotone sur un intervalle [a ; b] alors pour tout réel k compris entre f(a) et f(b) il existe un unique réel c de l’intervalle [a ; b] tel que f(c)=k .

Exemple :

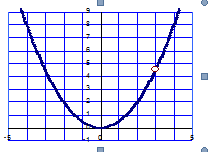
La courbe représentative de la fonction f est une parabole.

Le nombre réel  4 est une valeur intermédiaire entre f(0) et f(4)  et la fonction f est strictement croissante sur [0;4]  d’après le théorème des valeurs intermédiaires,  il existe un unique réel c vérifiant f(c)=4.

3.  Limites des fonctions

La notion de limite d’une fonction est assez intuitive. Mais elle est beaucoup plus difficile à formaliser mathématiquement. On veut donner un sens à la phrase :

f(x) tend vers  l quand x  tend vers a .

On entend par là que f (x) se rapproche de l “autant qu’on le souhaite”, pourvu que x soit “suffisamment proche” de a. Cela nous conduit à la définition suivante :

Définition: On dit que f (x) admet l pour limite quand x tend vers a et on note $\lim_{x \to a}f(x)$ ssi ∀ε > 0, ∃d > 0 tel que x vérifiant |x − a| ≤ d, on ait |f (x) − l| ≤ ε

ou encore

∀ε > 0, ∃d > 0 tel que pour tout x ∈ [a − d, a + d], on ait |f (x) − l| ≤ ε.

3.1 Limites usuelles

4. Limites par opérations

Dans tout ce qui suit, $\alpha$  désigne, soit un nombre réel, soit $+\infty$, soit $-\infty$ et L et L’ sont des nombres réels.

4.1.  Limite d’une somme

Définition : f et g étant deux fonctions définies sur le même intervalle I, leur somme f + g est la fonction définie sur I par

Théorème :

Exemples :    $f: x\mapsto (x^2 +\frac{1}{x})$ si $x \to -\infty$;$g : x\mapsto (x^2+x)$ si $x \to -\infty$ (indéterminé)

4.2.  Limite d’un produit

Définition : $f$ et $g$ étant deux fonctions définies sur le même intervalle I, leur produit $f g$ est la fonction définie sur I par $f\times g(x)=f(x)\times g(x) $

Théorème :

$h: x\mapsto 2x^3(\frac{1}{x}-3 ) $ si $x\to +\infty$   $k: x\mapsto 2x^2(x^2-1)$ si $x\to -\infty$ (indeterminé)

4.3.  Limite d’un quotient

Exemple :  $l:x\mapsto \frac{x-3}{1-x^2}$ si $x\to 1$ avec $x>1$ $p:x\mapsto \frac{1+4x^2}{x^2-9}$ si $x\to +\infty$

4.4.  Lever une indétermination.

Méthodes : Dans le cas où les théorèmes par opérations ne s’appliquent pas, on détermine une limite à l’infini d’une fonction polynôme ou rationnelle en transformant l’expression : dans chaque polynôme, on met en facteur la plus grande puissance de x et on simplifie pour appliquer les théorèmes.      

Dans le cas d’une fonction rationnelle $\frac{P(x)}{Q(x)}$ , pour lever une indétermination du type « $\frac{0}{0}$ » en une valeur a, on pose $x = a + h$ et on étudie la limite en 0 de la fonction de h obtenue.

Exemples

$g:x\mapsto (x^2 + x)$ si $ x\to -\infty$          

$ k:x\mapsto \frac{2}{x^2}{x^2-1}$ si $x\to -\infty$

$p:x\mapsto\frac{1+4x^2}{x^2 - 9}$ si $ x\to +\infty$  

$ t: x \mapsto \frac{2x^2-x-3}{6x^2+4x-2}$ si $ x \to -1 $

Théorème :

• La limite à l’infini d’un polynôme est égale à la limite de son monôme de plus haut degré :

$\lim\limits_{x\to \infty} ax^n+bx^{n-1}+ ... +c = \lim\limits_{x\to \infty} ax^n $

• La limite à l’infini d’une fonction rationnelle est égale à la limite du quotient des monômes de plus haut degré :

$\lim\limits_{x\to \infty} \frac{ax^n+bx^{n-1}+ ... +c}{\alpha x^p+\beta x^{p-1}+ ... +\delta} = \lim\limits_{x\to \infty}\frac{ax^n}{\alpha x^p} $

4.5. Asymptotes

Propriété : Soit $c$ un nombre réel. Si  $ \lim\limits_{x\to c} f(x) =+\infty$ (ou $-\infty$)  alors la droite d’équation $x=c $ est une asymptote « verticale »  à la courbe représentant la fonction f au voisinage de $c$

Exemple :

Propriété : Soit b un nombre réel. Si $ \lim\limits_{x\to +\infty} f(x) =b$ (ou $\lim\limits_{x\to -\infty} f(x) =b$) alors la droite d’équation y = b est une asymptote « horizontale » à la courbe représentant la fonction f au voisinage de $+\infty$ (ou $-\infty$ .

Remarque: On peut démontrer  que $ \lim\limits_{x\to +\infty} (f(x)-b) =0$ ( $ \lim\limits_{x\to -\infty} (f(x)-b) =0$

Exemple :

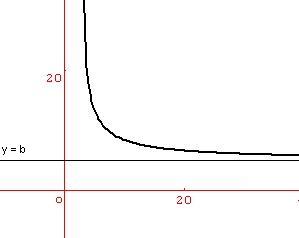
Propriété : Soient a et b deux nombres réels.

Si $ \lim\limits_{x\to +\infty} (f(x)-(ax+b)) =0$ alors la droite $\Delta$ d’équation $y = ax + b$ est une asymptote « oblique » à la courbe représentant la fonction f au voisinage de $+\infty$ (ou $-\infty$).

Exemple :

Corollaire : Si la fonction $f$ peut s’écrire $f(x)=ax+b +\phi (x)$ avec $ \lim\limits_{x\to \pm\infty} (\phi (x)=0$   alors la droite d’équation $y = ax + b$ est une asymptote « oblique » à la courbe représentant la fonction $f$ au voisinage de $\pm\infty$.

Remarques :

Pour connaître la position relative d’une courbe et de son asymptote oblique, on étudie le signe de la différence $f(x)-(ax+b)$ .

Une courbe peut traverser son asymptote horizontale ou oblique, mais jamais une asymptote verticale.

4.5.  Limites par comparaison

Théorème :

S’il existe un réel A tel que pour tout $x \geq A$, $f(x)\geq g(x)$ et  $ \lim\limits_{x\to +\infty} g(x) =+\infty$ alors $ \lim\limits_{x\to +\infty} f(x) =+\infty$.

Exemple : Soit f une fonction telle que pour tout $x\neq 0$, $f(x)\geq x^2+x-\frac{1}{x^2}$ , en déduire $ \lim\limits_{x\to +\infty} f(x)$ .

Théorème :

S’il existe un réel A tel que pour tout $x \geq A$, $f(x)\leq g(x)$ et $ \lim\limits_{x\to +\infty} g(x) =-\infty$  $ \lim\limits_{x\to +\infty} f(x) =-\infty$

Exemple : Soit f une fonction telle que pour tout $x\neq 2$, $f(x)\leq \frac{-2x^3+x-3}{2x^2-5}$ , en déduire $\lim\limits_{x\to +\infty} f(x)$ .

Théorème : (dit des gendarmes)

L désigne un nombre réel. S’il existe un réel A tel que pour tout $x\geq A$ , $u(x)\leq f(x) \leq v(x) $ et si $ \lim\limits_{x\to +\infty} u(x) =\lim\limits_{x\to +\infty} v(x) = L $    alors $ \lim\limits_{x\to +\infty} f(x) =L$

Exemple : Soit f une fonction telle que pour tout $x\geq 3$, $\frac{-x+2}{x^2+3}\leq f(x) \leq \frac{3x+1}{x^2-8}$, , en déduire $ \lim\limits_{x\to +\infty} f(x)$

Remarque : On dispose de théorèmes analogues quand x tend vers $-\infty$ en remplaçant $x\geq A$ par $x\neq A$ ou quand x tend vers un réel a.

Exemple : Soit k une fonction telle que pour tout $x\geq 0$,

$\frac{4x^2-4x+2}{x^2+1}\leq k(x) \leq \frac{4x^2+x+4}{x^2+2}$, , en déduire $ \lim\limits_{x\to +\infty} k(x)$  et $ \lim\limits_{x\to +0^+} k(x)$ .

4.6. Limite d’une fonction composée

Théorème :

$\alpha$, $m$ et $l$ désignent des nombres réels ou $+\infty$ ou $-\infty$

$ \lim\limits_{x\to +\infty} u(x)=m$ et $ \lim\limits_{x\to +\infty} v(x)=l $ donc $ \lim\limits_{x\to \alpha} v\circ u (x) =l$

Exemple

Soit f la fonction définie sur $\mathbb{R}$  par $f(x) = \sqrt{x^2+x+2}$ peut s’écrire sous la forme $ v \circ u $ avec $u(x) = x^2+x+1$ . et $v(x) = \sqrt{x}$ .

$ \lim\limits_{x\to -\infty} u(x)=+\infty$ et $ \lim\limits_{x\to +\infty} v(x)=+\infty $ donc $ \lim\limits_{x\to -\infty} f(x) =+\infty$