Bac maths, Etranger

 

La molécule de méthane $(CH_{4})$ a la forme d'un tétraèdre régulier de côté $a$ dont les sommets sont occupés par des atomes d'hydrogène et le centre est occupé par l'atome de carbone. On considère par la suite que chaque atome peut être assimilé à un point.

 

1. Sur la figure ci-après construire le centre de gravité $G$ du tétraèdre $ABCD.$

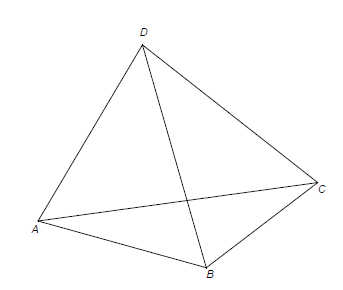
Montrez que la droite $(GD)$ est orthogonale au plan $(ABC).$ Soit $H$ le projeté orthogonal de $D$ (et donc de $G)$ sur $(ABC).$

 

Que peut-on dire de $H$ dans le triangle $(ABC)\ ?$

 

Montrez que $$GH=\dfrac{1}{4}DH$$

 

On note $I$ le milieu de $[AB]$.

 

2. Que peut-on dire du triangle $CID$ ? 

 

Calculez les distances $CI\;,\ CH\;,\ GH\;,\ GC$. 

 

Déduisez-en le cosinus de l'angle $\widehat{CGD}$ puis une valeur approchée en degrés de cet angle à $10^{-2}$ près.

 

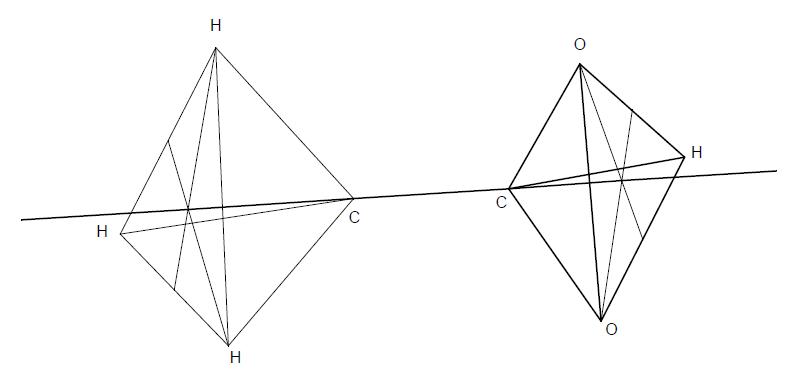
3. A la suite d'une expérience de chimie amusante on a remplacé un des atomes d'hydrogène par la molécule $(COOH)$ ce qui donne de l'acide acétique. La molécule a alors la forme de deux tétraèdres reliés par les deux atomes de carbone comme l'indique le schéma joint.

 

Sachant que l'atome de carbone a pour masse $12$, celui d'oxygène $16$ et celui d'hydrogène $1$ construire le centre de gravité de la molécule $(CH_{3}COOH)$ sur la figure suivante (les lettres représentent les divers atomes).

1. Pour construire le centre de gravité $G$ du tétraèdre $ABCD$ on construit le barycentre de $$\{(A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 1)\;,\ (D\;;\ 1)\}$$ 

 

Par ailleurs, $G$ est tel que $GA=GD=GB=GC$ et appartient aux plans médiateurs de $[AB]\;,\ [BC]$ et $[AC]$ ; ces trois plans sont perpendiculaires respectivement à $(AB)\;,\ (BC)$ et $(AC)$, l'intersection de ces trois plans est la droite $(GD)$ qui est donc perpendiculaire au plan $(ABC)$.

 

$H$ est à l'intersection des médiatrices dans le triangle $(ABC)$ qui est équilatéral ; c'est le centre de ce triangle.

 

En prenant le barycentre $H$ de $\{(A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 1)\}$, on a $G$ barycentre de $\{(H\;;\ 3)\;,\ (D\;;\ 1)\}$ et donc $\overrightarrow{HG}=\dfrac{1}{4}\overrightarrow{HD}\;,$ soit $GH=\dfrac{1}{4}DH.$

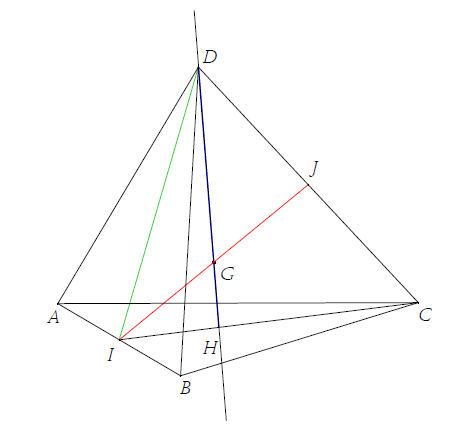
2. $CID$ est isocèle et $CI=ID$.

 

Comme les triangles $ABC\;,\ CBD$, etc. sont équilatéraux, $$CI=ID=a\dfrac{\sqrt{3}}{2}$$

 

$H$ est le centre de gravité de $ABC$ donc $$CH=\dfrac{3}{2}a\dfrac{\sqrt{3}}{2}=a\dfrac{\sqrt{3}}{3}$$

$DHC$ est rectangle en $H$ donc :

 

$\begin{array}{rcl} CH^{2}+DH^{2}=DC^{2}&\Leftrightarrow&DH^{2}=a^{2}-a^{2}\dfrac{3}{9}=a^{2}\dfrac{2}{3} \\ \\ &\Leftrightarrow&DH=a\dfrac{\sqrt{6}}{3}\end{array}$ 

 

On en tire $$GH=\dfrac{1}{4}DH=a\dfrac{\sqrt{6}}{12}$$ enfin $$GC=GD\dfrac{3}{4}DH=a\dfrac{\sqrt{6}}{4}$$

 

Avec Al-Kashi :

 

$\begin{array}{rcl} \cos\widehat{CGD}&=&\dfrac{CD^{2}-GC^{2}-GD^{2}}{-2GC.GD} \\ \\ &=&\dfrac{a^{2}\left(1-\dfrac{6}{16}-\dfrac{6}{16}\right)}{-2a^{2}\dfrac{6}{16}.\dfrac{6}{16}} \\ \\ &=&\dfrac{\dfrac{1}{4}}{-\dfrac{9}{32}} \\ \\ &=&-\dfrac{8}{9} \\ \\ \Rightarrow\ \widehat{CGD}&\approx&152.73^{o}\end{array}$

 

3. On construit le centre de gravité de gauche, $G_{1}\ :\ \{(H\;;\ 1)\;,\ (H\;;\ 1)\;,\ (H\;;\ 1)\;,\ (C\;;\ 12)\}$ qui aura la masse 15 et celui de droite, $G_{2}\ :\ \{(H\;;\ 1)\;,\ (O\;;\ 16)\;,\ (C\;;\ 12)\}$ qui aura la masse $45.$ 

 

Le centre de gravité de la molécule sera en $G$ tel que $$\overrightarrow{G_{1}G}=\dfrac{45}{64}\overrightarrow{G_{1}G}_{2}$$