Corrigé Bac Maths S1 1er groupe 2015
Exercice 1
1) a) Il suffit de l'écrire.
b) Soit k un entier non nul et T=(p, q, r) un triplet d'entiers relatifs tel que r non nul.
T∈Γ⇔p2+q2=r2⇔(kp)2+(kq)2=(kr)2⇔kT∈Γ
2) a) Posons T1=(p1, q1, r1) et T2=(p2, q2, r2). Alors.
→OM1⋅→OM2=p1p2+q1q2||→OM1∧→OM2||=||(p1q2p2q1)→k||=|p1q2−p2q1|et ||→OM1||×||→OM2||=r1r2
sont bien des entiers. Ensuite
(→OM1⋅→OM2)2=||→OM1||2×||→OM2||2cos2θ||→OM1∧→OM2||2=||→OM1||2×||→OM2||2sin2θ
Donc
(→OM1⋅→OM2)2+||→OM1∧→OM2||2=(||→OM1||×||→OM2||)2
et T1∗T2∈Γ.
Ou bien :
(→OM1⋅→OM2)2+||→OM1∧→OM2||2=(p1p2+q1q2)2+|p1q2p2q1|2=p21p22+q21q22+p21q22+p22q21=(p21+q21)(p22+q22)=r21r22=(||→OM1||×||→OM2||)2
b) Le triplet T1∗T2 est trivial si et seulement si →OM1⋅→OM2=0 (c'est à dire (OM1) et (OM2) sont perpendiculaires) ou →OM1∧→OM2=0 (c'est à dire →OM1 et →OM2 sont colinéaires donc, (OM1) et (OM2) sont confondues).
c) Notons M′ et M″ les points associés au triplets T′ et T″.
Alors,
S′=T′∗T″=(|→OM′⋅→OM″|, ||→OM′∧→OM″||, ||→OM′||×||→OM″||)=(63, 16, 65)
appartient à Γ et il est irréductible.
T″0=(−5, 12, 13) est aussi un élément de Γ; notons M″0 le point associé au triplet T″0.
Alors,
S″=T′∗T″0=(|→OM′⋅→OM″0|, ||→OM′∧→OM″0||, ||→OM′||×||→OM″0||)=(33, 56, 65)
appartient à Γ et il est irréductible.
Notons N′ et N″ les points associés au triplets S′ et S″.
Alors,
S′∗S″=(|→ON′⋅→ON″|, ||→ON′∧→ON″||, ||→ON′||×||→ON″||)=(2975, 3000, 4225)
appartient à Γ mais est réductible. Le triplet irréductible correspondant est (119, 120, 169).
on obtient d'autres triplets en combinant par exemple T′ et S′ ou T″ et S′ etc...
Exercice 2
1) A′ appartient à (C) car la droite (OM) est un axe de symétrie de ce cercle.
De plus (→OA, →OA′)=2(→OA, →OM)=2θ [2π].
C appartient à (C) et (→OA, →OC)=2θ+π [2π].
Il vient : (→OA′, →OC)=(→OA′, →OA)+(→OA, →OC)=π [2π]
Donc A′ et C sont bien symétriques par rapport à O.
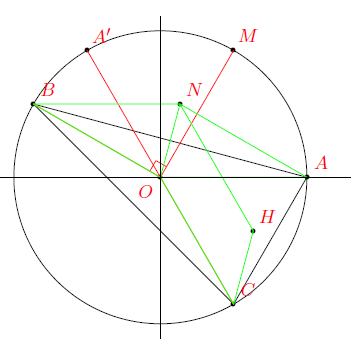
2) a) b=ei(θ+π2)=eiπ2.eiθ=iz et c=ei(2θ+π)=eiπ.e2iθ=−z2.
b) →ON=→OA+→OB; donc N est le quatrième sommet du parallélogramme dont trois points consécutifs sont B, O et A.
→OH=→ON+→OC; donc H est le quatrième sommet du parallélogramme dont trois points consécutifs sont C, O et N.
3) a) θ est différent de π2 [π] signifie que z est différent de i et de −i
Alors b=iz différent de 1 (et de -1) ; A et B sont donc distincts.
De même c=−z2 différent de 1 (et de -1) ; A et C sont donc distincts.
Enfin b−c est différent de 0 (et de -2) ; par conséquent B et C sont distincts.
z→AHz→CB=b+cb−c=iz−z2iz+z2=1−iz1+iz et z→CHz→BA=1+b1−b=1+iz1−iz
Ensuite :
1+iz1−iz=1+e2iα1−e2iα avec α=θ2+π4=e−iα+eiαe−iα−eiα=cosαsinαi est bien imaginaire pur
On en déduit que les angles (→AH, →CB) et (→CH, →BA) sont droits ; H est donc l'intersection des hauteurs c'est à dire l'orthocentre du triangle ABC.
b) Le discriminant de l'équation est i2+4=3. Les racines de l'équation sont donc z1=i+√32=eiπ6 et z2=i−√32=e5iπ6
Le centre de gravité G du triangle ABC est 13(1+b+c).
Pour que H coïncide avec G il faut et il suffit que 1+b+c soit égale à 13(1+b+c) c'est à dire que 1+b+c=0 ou z2−iz−1=0. Donc H coïncide avec G si et seulement si θ=π6 ou θ=5π6
4) Puisque l'affixe z s'écrit cosθ+isinθ, celle de H s'écrit :
1+iz−z2=1+i(cosθ+isinθ)−(cosθ+isinθ)2=1−sinθ+icosθ−cos2θ−isin2θ formule de Moivre =1−sinθ−cos2θ+i(cosθ−sin2θ)
Donc H est le point de (H) de paramètre θ.
Problème
Partie A
1) a) la fonction f est définie et continue sur [0, 1[.
Elle est dérivable dans cet intervalle et ∀x∈[0, 1[, f′(x)=−2x−11−x
La dérivée, somme de deux réels négatifs dont l'un l'est strictement, est strictement négative. f(0)=1 et limx→1−f(x)=−∞.
Voici le tableau de variation de f.
x01f′(x)−1f(x)↘−∞
La fonction f est strictement décroissante et envoie l'intervalle [0, 1[ sur l'intervalle [−∞, 1[ qui contient 0, donc l'équation f(x)=0 a une solution unique α.
b) f(12)=34−ln2>0 et f(β)=−β2<0 ; donc d'après le théorème des valeurs intermédiaires, α appartient à l'intervalle ]12, β].
2) Posons pour simplifier Iβ=]12, β].
f est deux fois dérivable dans [0, 1[ et ∀x∈[0, 1[, f″(x)=−2−1(1−x)2
Alors, ∀x∈Iβ, p(x)=2x+11−x et q(x)=2+1(1−x)2
p et q sont dérivables sur Iβ et ∀x∈Iβ, p′(x)=2+1(1−x)2 et q′(x)=1(1−x)3
Ces dérivés sont positives.
Voici les tableaux de variation de p et q.
x1/2βp′(x)+p(β)p(x)↗3
x1/2βq′(x)+e2+2q(x)↗6
Ces tableaux montrent clairement que ∀x∈Iβ, 3≤|f′(x)| et |f″(x)|≤e2+2
ce qui entraîne bien ∀x, y∈]12, β], |f″(x)||f′(y)|≤e2+23=M
3) a) On peut procéder à une IPP en posant u=ln(1−x) et v=1−x, il vient u′=−11−x et v′=−1 puis ∫tαln(1−x)dx=−∫tαuv′dx=−[uv]tα+∫tαu′vdx=[−x−(1−x)ln(1−x)]tα
Il est probable que le candidat fasse le changement de variable 1−x=u pour se ramener à ∫lnudu=ulnu−u. Il peut aussi faire une IPP en posant u=ln(1−x) et v′=1 et s'il choisit v=x, il devra trouver une primitive de x1−x en procédant à une réduction en éléments simples
b) ∫tαf(x)dx=∫tα(1−x2)dx+∫tαln(1−x)dx Donc ∫tαf(x)dx=φ(t)−φ(α), avec φ(x)=−13x3−(1−x)ln(1−x)
Lorsque t tend vers 1−, (1−t)ln(1−t) a pour limite 0, donc limt→1−∫tαf(x)dx=−13−φ(α)
Mais f(α)=0 signifie ln(1−α)=α2−1
limt→1−∫tαf(x)dx=P(α), avec P(x)=−23x3+x2+x−43
Partie B
1) a) La tangente en A à Ch a pour équation y=h′(a)(x−a)+h(a). l'intersection de cette tangente avec l'axe des abscisses a pour ordonnée 0, son abscisse x est donc telle que h′(a)(x−a)+h(a)=0 c'est à dire x=a−h(a)h′(a)=T(a).
b) T, rapport de deux fonctions dérivables, est dérivable et ∀x∈J, T′(x)=1−(h′(x))2−h(x)h″(x)(h′(x))2=h(x)h″(x)(h′(x))2
T′ est donc positive sur J.
Mais T(v)=v−h(v)h′(v) est ≤v car le rapport h/h′ est ≥0; donc T(J)=[u, T(v)]⊂[u, v]=J.
Voici le tableau de variation de T.
xuvT′(x)+T(v)T(x)↗u
2) a) Montrons que la suite (xn) est bien définie et contenue dans J donc bornée.
Par récurrence. x0=v existe et appartient à J.
Si la propriété est vraie pour un rang n donné, c'est à dire si xn existe et appartient à J alors, xn+1=T(xn) existe et appartient bien à J car T(J) est contenu dans J. Donc la propriété est vraie au rang suivant n+1.
b) ∀n∈N, xn+1=T(xn)=xn−h(xn)h′(xn) est ≤xn car le rapport h/h′ est ≥0; donc la suite (xn) est décroissante. Comme elle est minorée par u, elle converge vers un réel l≥u.
Puisque ∀n∈N, xn+1=T(xn) on obtient par passage à la limite T(l)=l c'est à dire l−h(l)h′(l)=l ou h(l)=0. Comme u est l'unique zéro de h, l=u. limn→+∞xn=u
Partie C
1) a) G(a)=0.
b) G(b)=0 est équivalent à : 0=g(a)−g(b)−(a−b)g′(b)−12k(a−b)2.
C'est à dire k=2(a−b)2(g(a)−g(b)−(a−b)g′(b)).
2) a) La fonction G satisfait aux hypothèses du théorème des accroissements finis dans l'intervalle [a, b] ;
donc il existe un réel c dans l'intervalle ]a, b[ tel que G(b)−G(a)=G′(c)(b−a) c'est à dire G′(c)=0.
b) On a pour tout x dans [a, b], G′(x)=−(a−x)g″(x)+k(a−x).
G′(c)=0 est donc équivalent à : k=g″(c) c'est à dire
2(a−b)2[g(a)−g(b)−(a−b)g′(b)]=g″(c)ou g(a)−g(b)−(a−b)g′(b)=12(a−b)2g″(c)enfin g(a)=g(b)+(a−b)g′(b)+12(a−b)2g″(c)
3) a) D'après les calculs faits dans la première partie, la fonction f satisfait bien dans l'intervalle [α, β] aux hypothèses faites sur h.
b) Pour tout entier naturel n, cette même fonction f satisfait, dans l'intervalle [α, xn], aux hypothèses faites sur g. On a donc : ∀n∈N, ∃cn∈]α, xn[;f(α)=f(xn)+(α−xn)f′(xn)+12(α−xn)2f″(cn)(∗)
4) Pour obtenir la relation (xn+1−α)=(xn−α)2f″(cn)2f′(xn)(∗∗)
il suffit de se rappeler que f(α)=0 et de diviser la relation (∗) par le réel non nul f′(xn).
il suffit de se rappeler que f(α)=0 et de diviser la relation (∗) par le réel non nul f′(xn).
D'après la première partie, puisque xn et cn appartiennent à Iβ, |f″(cn)||f′(xn)|≤M, et (∗∗) entraîne (xn+1−α)≤M2(xn−α)2
5) Si on pose ∀n∈N, δn=M2(xn−α), la relation 0≤(xn+1−α)≤M2(xn−α)2 se traduit par 0≤δn+1≤δ2n.
Montrons que δn≤δ2n0≤(M4)2n.
Par récurrence.
Cette propriété est vraie au rang 0 car à ce rang elle signifie δ0≤δ0≤M4
Si elle est vraie pour un rang donné n c'est à dire si δn≤δ2n0≤(M4)2n, alors δn+1≤δ2n≤(δ2n0)2=δ2n+10≤(M4)2n+1
Elle est donc vraie au rang suivant n+1.
6) Pour tout entier naturel n on a les implications suivantes :
xn−α≤10−5⇔2Mδn≤10−5⇔δn≤M2×105⇐(M4)2n≤M2×105⇔2nlnM4≤lnM2×105⇔2n≥ln(M2×105)ln(M4) car M4<1⇔nln2≥ln(ln(M2×105)lnM−ln4)⇔n≥1ln2ln(lnM−ln(2×105)lnM−ln4)∼5.4949
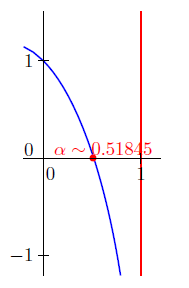
On peut prendre n=6

Ajouter un commentaire