Corrigé de la composition du premier semestre

Exercice n°1 :

Pour chacune des questions suivantes une seule des quatre réponses proposées est exacte.
Indiquer la bonne réponse.

1. $A, B, C$ et $D$ sont quatre points alignés tels que$\vec{CA}.\vec{CB} < 0$ et $\vec{AB}.\vec{CD}> 0$. Alors

    a) $D ∈ [AB)$     b) $D∈ [BD)$      c) $D ∈ [AC)$      d) $D ∈ [CB)$

La relation $\vec{CA}.\vec{CB} < 0$ signifie que les vecteurs $\vec{CA}$ et $\vec{CB}$ sont de sens contraires, donc que $C$ est sur le segment $[AB]$.

La relation $\vec{AB}. \vec{CD}> 0$ signifie que les vecteurs $\vec{AB}$ et $\vec{CD}$ sont de même sens. Donc $D$ est sur la demi-droite $[CB)$.
Bonne réponse : d.

2. Soient $\vec{u} , \vec{v}$ et $\vec{w}$ trois vecteurs du plan tels que : $\vec{u}⊥\vec{w}$ et $\vec{v}⊥\vec{w}$ . Alors
     a) $\vec{u}  ⊥\vec{v}$      b) $\vec{u} = \vec{0}$ ou $\vec{v} = \vec{w}$      c) $\vec{w}$ et $( − \vec{v} )$ sont orthogonaux
     d) $\vec{w}$ et $(\vec{u} −\vec{v} )$ sont colinéaires.

Si on a à la fois $\vec{u} ⊥\vec{w}$ et $\vec{v}⊥\vec{w}$ , cela se traduit par les égalités $\vec{u}  = 0$ et $\vec{v} . \vec{w} = 0$ qui entraînent par différence membre à membre, et d’après les propriétés du produit scalaire que : $(\vec{u}  − \vec{v} ) . \vec{w} = 0$Donc $(\vec{u}  − \vec{v} )$ et $\vec{w}$ sont orthogonaux.
Bonne réponse : c.

3. $EFG$ est un triangle équilatéral de centre $O$ tel que $EF = 6$. Alors $\vec{OE} . \vec{EF} =$
     a) $12$      b) $-12$      c) $-18$      d) $18$

$\vec{OE} . \vec{EF} = \vec{OE} . \vec{EE′}$ (par projection orthogonale du vecteur $\vec{EF}$ sur le vecteur $OE$ ). (Or par application du théorème de PYTHAGORE dans le triangle $EE’F$, on a : $EE′ = \sqrt{6^{2} − 3^{2}} = 3\sqrt{3}$Par suite, $\vec{OE} . \vec{EF} = −\dfrac{2}{3}EE^{′2} == −\dfrac{2}{3}× 27 = −18$.
Bonne réponse : c.

4. Si $ABCD$ est un carré de côté $a > 0$, alors $\vec{DC} .\vec{BD} =$
     a) $−a^{2}$      b) $a\sqrt{2}$      c) $−a\sqrt{2}$      d) $a^{2}$

$\vec{DC} .\vec{BD} = \vec{DC} . \vec{CD} = −a^{2}$.
Bonne réponse : a.

5. Si $\vec{u} $et $\vec{v}$ sont deux vecteurs colinéaires, de sens contraires, tels que $‖\vec{u} ‖ = 2$ et $‖\vec{v} ‖ = 1$,alors $(\vec{u} + 3\vec{v} )^{2}$ est égal à :
    a) $1$      b) $5$      c) $13$      d) $25$

$(\vec{u} + 3\vec{v})^{2} = ‖\vec{u} ‖^{2} + 6 \vec{u} . \vec{v} + 9‖\vec{v} ‖^{2}$. Or $\vec{u} . \vec{v} = −‖\vec{u} ‖‖\vec{v} ‖ = −2$. D’où :

$(\vec{u} + 3v )^{2} = 4 − 12 + 9 = 1$
Bonne réponse : a.

6. Soit $f$ la fonction définie par $f(x) =\dfrac{\sqrt{1−x^{2}}}{|x|−1}$. Alors l’ensemble de définition de $f$ est :

     a)$[−1; 1]$\ $\{ 0 \}$      b) $]−1; 1[$      c) $[−1; 1]$      d) $]−∞; −1[ ∪ ]1; +∞[$

$f(x)$ existe si et seulement si
$$\left\lbrace\begin{array}{rcl}
1 − x^{2} &≥& 0\\
|x| &≠& 1 \text{  }
Df = ]−1; 1[.
\end{array}\right.$$

Bonne réponse : b.

Exercice n°2 :

Soit $ABDC$ un carré de côté a $(a > 0), E \in [AB], F \in [AD]$ tels que $AE = AF = ka$ avec $0 < k < 1$
1°) Exprimer en fonction de $a$ et $k : \vec{AC}.\vec{AB} ; \vec{BF}.\vec{EA} ; \vec{BF}.\vec{AD}$ et $\vec{BF}.\vec{ED}
\vec{AC}.\vec{AB} = (\vec{AB} + \vec{BC} ).\vec{AB}$ (par la relation de CHASLES) = $AB^{2} + \vec{BC}. \vec{AB}$ (par la propriété de distributivité du produit scalaire) $= AB^{2}$ (car $\vec{ BC}$ et $\vec{AB}$ sont orthogonaux) $= a^{2}$.
$\vec{BF} . \vec{EA} = (\vec{BA} + \vec{AF} ).\vec{EA} = \vec{BA}$ .

$\vec{EA} + \vec{AF} .\vec{EA} = \vec{BA}.\vec{EA}$ (car $\vec{AF}$ et $\vec{EA}$ sont orthogonaux)

$= BA × EA$ (car les vecteurs $\vec{BA}$ et$\vec{EA}$ sont colinéaires et de même sens) $= a\times ka = ka^{2}$.

$\vec{BF} .\vec{AD} = (\vec{BA}+\vec{AF}). \vec{AD}=\vec{BA}.\vec{AD} + \vec{AF}.\vec{AD} = 0 + \vec{AF}.\vec{AD} = ka^{2}\\
\vec{BF} . \vec{ED} = \vec{BF} . (\vec{EA} + \vec{AD} ) = ka^{2} + ka^{2} = 2ka^{2}$ (d’après les deux calculs précédents).

2°) Soit $I$ le milieu de $[BF]$.

a) Exprimer $\vec{AI}$ en fonction de $\vec{AB}$ et $\vec{BF}$

b) Exprimer $\vec{ED}$ en fonction de ⃗$\vec{AE}$ et $\vec{AD}$

c) Montrer que la médiane issue de $A$ du triangle $ABF$ est la hauteur relative au côté $[DE]$ du
triangle $EAD$

2°) a) $\vec{AI} =\dfrac{1}{2}(\vec{AB} + \vec{AF} )$ (propriété caractéristique du milieu d’un segment) $=\dfrac{1}{2}(\vec{AB} + \vec{AB} + \vec{BF})$ (relation de CHASLES dans $\vec{AF} )= \vec{AB} +\dfrac{1}{2}\vec{BF}$

b) $\vec{ED} =\vec{EA} + \vec{AD} = −\vec{AE} + \vec{AD}$

c) Il s’agit de montrer que $\vec{AI}$ et $\vec{ED}$ sont orthogonaux. Or, d’après les calculs précédents,

$\vec{AI}.\vec{ED} = (\vec{AB} +\dfrac{1}{2}\vec{BF} ) . (−\vec{AE} + \vec{AD} ) = −\vec{AB} .\vec{AE} + \vec{AB}.\vec{AD} −\dfrac{1}{2}\vec{BF}.\vec{AE} +\dfrac{1}{2}\vec{BF} .\vec{AD} = −ka^{2} + 0 +\dfrac{ka^{2}}{2}+\dfrac{ka^{2}}{2}= 0$
D’où le résultat

Probleme 1

Soit $\vec{v}$ l'ensemble des vecteurs du plan $P$

Soit $ABC$ un triangle isocèle en $A,H$ le pied de la hauteur issue de $A$ tel que $AH=BC=4cm$ et $n$ un entiers relatif.On considère l'application $f$ définie par:$P\Longleftrightarrow\vec{v}$

$f_{n}:M\Longleftrightarrow\vec{f_{n}(M)}=\vec{2MA}+n\vec{MB}+n\vec{MC}$

Soit $G_{n}$ le barycentre,lorsqu'il existe,du système des points ${(A,2);(B,n)(C,n)}$

1.Déterminer les valeurs de $n$ pour lesquels $G_{n}$ défini

2.Déterminer $\vec{f_{n}(A)}$ et $\vec{f_{n}(H)}$

3.Montrer que $\vec{f}_{n}$ est constante

4.Montrer que $\vec{f}_{n}$ est injective

5.L'application $\vec{f}_{n}$ est - elle surjective

6.Déterminer l'image réciproque de $\vec{O}$

7.On considère maintenant l'application $\vec{f}_{2}$

a-Déterminer la position du point $G_{2}$

b-Quelle est l'image réciproque de $\dfrac{2}{3}\vec{HA}$

c-Déterminer l'image réciproque de $-\dfrac{1}{6}\vec{HA}$

d-Déterminer l'image directe du point $H$

8-Déterminer la nature de l'ensemble es points $M$ tel que $||\vec{f_{-1}}(M)=\vec{f_{-1}}(M)||$

   Bonne réponse : Probleme 1

$G_{n}$ est défini si et seulement la somme des coefficients, soit $2 + 2n$ est non nulle. Donc il est
défini pour $n \in\mathbb{Z} \ {−1}$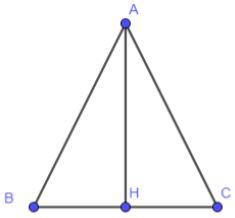

2. $\vec{f_{n}(A)}= n\vec{AB} +n\vec{AC}=2n\vec{AH}$

3. $\vec{f^{−1}(M)}=2\vec{MA}- \vec{MB}- \vec{MC}$ Or, $-\vec{MB}- \vec{MC}=2\vec{MH}$(propriété caractéristique du milieu d’un segment).

Donc$\vec{f^{−1}(M)}=2\vec{MA}- 2\vec{MH}- 2\vec{HA}
f^{−1}$ est bien constante.

4. Soit $\vec{u}$un vecteur donné de $\vec{v}$. Existe-t-il un point $M$ du plan $P$ tel que : $\vec{f_{n}(M)}=\vec{u}$? (*)

Si $n = −1$, le vecteur $\vec{u}= 2\vec{AH}$ a une infinité d’antécédents (car tout point $M$ du plan est alors tel que $\vec{f_{n}(M)} =2\vec{AH})$ et les autres vecteurs n’ont aucun antécédent. Ainsi $\vec{f_{n}}$ n’est pas injective dans ce cas !

Si $n \ne −1$ : Alors, d’après la propriété de réduction, on a : $\vec{f_{n}(M) }= (2n + 2)MG_{n}$ . Or, étant donné un vecteur $\vec{u}$, il existe d’après l’Axiome d’Euclide un unique point $M$ tel que
$MG_{n}=\dfrac{1}{2n + 2}\vec{u}$en d’autres termes tel que :$\vec{f_{n}(M)}=\vec{u}$ Dans ce cas, $\vec{f_{n}}$ est non seulement injective, mais même bijective !

5. On a répondu à cette question au passage dans
4°.
6. L’image réciproque de $O$ n’est autre que $G_{n}$.

7°) a)$G_{2}$ est le barycentre du système
${(A, 2), (B, 2), (C, 2)}$ donc il n’est autre que le centre de gravité du triangle $ABC$.

b)$\vec{f_{2}(M)}=\dfrac{2}{3}\vec{AH}\Longleftrightarrow 8\vec{MG_{2}}=\dfrac{2}{3}\vec{AH}=\vec{AG_{2}}\Longleftrightarrow\vec{MG_{2}}=\dfrac{1}{6}\vec{AG_{2}}$L’image réciproque de $\dfrac{2}{3}\vec{AH}$ est le point $M$ du segment $[AH]$ caractérisé par cette relation.

c) $\vec{f_{2}(M)}=\dfrac{1}{6}\vec{HA}\Longleftrightarrow6\vec{MG_{2}}=\dfrac{1}{6}\vec{AH}=\dfrac{1}{12}\vec{AG_{2}}$ L’image réciproque de $-\dfrac{1}{6}\vec{HA}$ est le point $M$ du segment $[AH]$ caractérisé par cette relation.

d) $\vec{f_{2}}(H) = 6\vec{HG_{2}}= 2\vec{HA}$

8°)$ ||\vec{f_{n}(M)}|| = 2n\vec{f_{-1}(M) }||\Longleftrightarrow(2 + 2n)||MG_{n}\dfrac{2n}{2+2n}HA =\dfrac{n}{n+1}HA$ Et comme $HA = 4 cm$, l’ensemble cherché est le
cercle de centre $G_{n}$ et de rayon $\dfrac{4n}{n+1}cm$.

Bonne réponse :Probleme 2

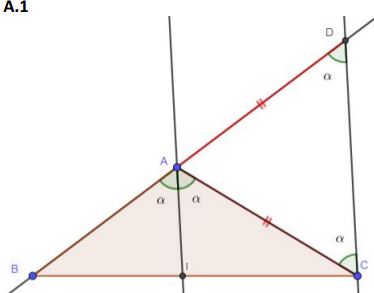
1°) Les angles $I\overbrace{A}C$ et $\overbrace{ACD}$ sont égaux comme
angles alternes-internes (parallèles $(IA)$ et $(CD)$
coupées par la sécante $(CA))$.
Les angles $\overbrace{BA}I$ et $\overbrace{AD}C$ sont aussi égaux comme
angles correspondants (considérer les parallèles $(IA)$ et $(CD)$ coupées par la sécante $(BD)$).
Comme $\overbrace{BA}I =I\widehat{A}C$ par hypothèse (car $(AI)$ est
une bissectrice), il en résulte que $\overbrace{ADC} = \overbrace{ACD}$ :
ainsi, dans le triangle $ACD$ les angles en $C$ et en $D$ sont égaux. Ce triangle est donc isocèle en $A$. En d’autres termes, on a $AC = AD$.
En appliquant le théorème de THALES aux triangles $BAI$ et $BDC$, on a :
$\dfrac{IB}{IC}=\dfrac{AB}{AD}=\dfrac{AB}{AC}=\dfrac{c}{b}$
2°) $I$ étant un point du segment $[BC]$, il existe unréel $k < 0$ tel que $\vec{IB} =K \vec{IC}$ . En prenant les normes des deux membres, on en déduit que :
$||\vec{IB}||= ||K \vec{IC} || = |k| × ||\vec{IC}|| = −k‖\vec{IC}||$.
Par suite, on a :
$\dfrac{IB}{IC}= −K$, et compte tenu de l’égalité du a), $K = −\dfrac{c}{b}$.Ainsi $\vec{IB}=K \vec{IC}= −\dfrac{c}{b}\vec{IC}$ , d’où il résulte, par
multiplication par$b$ que :
$B \vec{IB}+ C \vec{IC} =\vec{O}$ .

On en conclut que le point I, intersection de la bissectrice de l’angle $\overbrace{A}$ et du côté $[BC]$ du triangle $ABC$ est le barycentre du système ${ (B, b), (C, c)}$.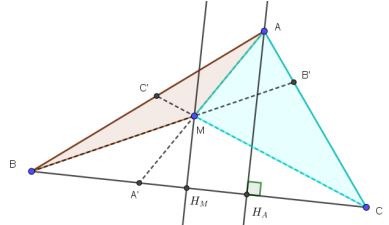

De manière analogue, on démontrerait que les points $J$ et $K$, points d’intersection respectifs de la bissectrice de l’angle $\overbrace{B}$avec le côté $[AC]$ du
triangle ABC et de la bissectrice de l’angle $\overbrace{C}$ avec le côté $[AB]$ du triangle ABC sont les barycentres dessystèmes ${ (A, a), (C, c)}$ et ${ (A, a)), (B, b)}$ respectivement.

3°) En utilisant l’associativité du barycentre, on monte que le barycentre de ${(A, a)), (B, b), (C, c)}$ appartient à la fois à $(IA), (JB)$ et $(KC)$, c’est-à-dire aux trois bissectrices du triangle $ABC$ : c’est le centre du cercle inscrit.
1°) a) On a, avec les notations de la figure ci-dessous :
aire $(ABA’) = \dfrac{A′B}{AH_{A}}$ et aire $(ACA’) = \dfrac{A′C}{AH_{A}}$, d’où $\dfrac{aire (ABA′)}{aire (ACA′)}=  \dfrac{A′B}{A'C}$. (1)

Mais on a aussi : aire$ (MBA’) = \dfrac{A′B}{MHM}$et $aire (MCA’) = \dfrac{A′C}{MHM}$, d’où $\dfrac{aire (MBA′)}{aire (MCA′)}= \dfrac{A′B}{A′C}$. (2)
Or, on a la propriété classique suivante des rapports égaux :
Or, on a la propriété classique suivante des rapports égaux :
Si $\dfrac{a}{b}=\dfrac{c}{d}$
, alors on a aussi :
$\dfrac{a}{b}=\dfrac{c}{d}= \dfrac{a−c}{b−d}$.
L’égalité (3) entraîne donc que :
$\dfrac{aire (ABA′)}{aire (ACA′)}=\dfrac{ aire (MBA′)}{aire (ACA′)}= \dfrac{aire (ABA′)−aire (MBA′)}{aire (ACA′)−aire (MCA′)}$,ce dernier rapport étant égal à $\dfrac{aire (MAB)}{aire (MAC)}$.

Il résulte de toutes ces égalités que :
$\dfrac{aire (MAB)}{aire (MAC)}= \dfrac{A'B}{A'C}$ .

b) b) $A′$ étant un point du segment $[BC]$, il existe un réel $k < 0$ tel que $\vec{A′B} = K \vec{A′C}$. En prenant les normes des
deux membres, on en déduit que :$ ||A'B|| = ||K \vec{A'C} || =|K| × || \vec{A'C} || = −k‖ \vec{A'C} ||$.
Par suite, on a :
$\dfrac{A'B}{A'C}= −K$, et compte tenu de l’égalité du
a), $K = −\dfrac{aire (MAB)}{aire (MAC)}$.
Ainsi $\vec{A′B}= K \vec{A'C}= −\dfrac{aire (MAB)}{aire (MAC)}\vec{A'C}$, d’où il résulte, par multiplication par aire (MAC) que :
$aire (MAC) \vec{A'B} + aire (MAB) \vec{A'B}=\vec{O} $. C.Q.F.D

2°) On vient de montrer que :
• $A '$ est le barycentre des points pondérés $(B, aire (MAC) )$ et $(C , aire(MAB) )$ .
De manière analogue, on montre que

• $B '$ est le barycentre des points pondérés $(A, aire (MBC) )$ et $(C , aire(MBA) )$ .

• $C '$ est le barycentre des points pondérés $(C, aire (MCA) )$ et $(b , aire(MCB) )$ .

3°) Soit alors $G$ le barycentre de ${(A, aire(MBC); (B, aire (MAC)); (C , aire(MAB) )}$.

Alors, en appliquant à $G$ la propriété d’associativité du barycentre trois fois, on a :

$G = bar {(A, aire(MBC); (A′, aire (MAC) + aire(MAB))}\longleftarrow G, A$ et $A’$ sont alignés.

$G = bar {(B, aire(MAC); (B′, aire (MBC) + aire(MAB))}\longleftarrow G, B$ et $B’$ sont alignés.
$G = bar {(C, aire(MAB); (c, aire (MAC) + aire(MBC))}\longleftarrow G, C$ et $C’$ sont alignés.

Il en résulte que G est le point d’intersection des droites $(AA’), (BB’) et (CC’)$, en d’autres termes, $G = M$.