I. Définition et propriétés
I.1 Définition
On appelle racine carrée d'un nombre réel positif $a$ le réel noté $\sqrt{a}$ dont le carré est égal à $a$.
I.2 Propriétés
$\centerdot\ \ (\sqrt{a})^{2}=a$
$\centerdot\ \ \sqrt{a^{2}}=|a|$
$\centerdot\ \ a\geq 0\ ,\ b\geq 0\ ;\qquad \sqrt{ab}=\sqrt{a}\times\sqrt{b}$
$\centerdot\ \ a\geq 0\ ,\ b>0\ ;\qquad \sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}$
$\centerdot\ \ x^{2}=a\ $ avec $a$ positif $\Rightarrow\ x=\sqrt{a}\ $ ou $x=-\sqrt{a}$
Attention :
$\sqrt{a+b}\neq\sqrt{a}+\sqrt{b};\qquad$ $\forall a>0,\ b>0$
Exemple 1 :
Donnons une écriture plus simple des expressions suivantes
$\begin{array}{rcl} A&=&5\sqrt{25\times 6}-8\sqrt{36\times 6}+6\sqrt{6}-7\sqrt{100\times 6}\\ \\&=&5\sqrt{25}\times\sqrt{6}-8\sqrt{36}\times\sqrt{6}+6\sqrt{6}-7\sqrt{100}\times\sqrt{6}\\ \\& = &25\sqrt{6}-48\sqrt{6}+6\sqrt{6}-70\sqrt{6}\\ \\&=&(25-48+6-70)\sqrt{6}\\ \\&=&-87\sqrt{6}\end{array}$
D'où, $$\boxed{A=-87\sqrt{6}}$$
$\begin{array}{rcl} B&=&\dfrac{5}{3}\sqrt{108}-\dfrac{4}{5}\sqrt{432}+\dfrac{3}{2}\sqrt{243}-\dfrac{1}{3}\sqrt{75}\\ \\&=&\dfrac{5}{3}\sqrt{36\times 3}-\dfrac{4}{5}\sqrt{144\times 3}+\dfrac{3}{2}\sqrt{81\times 3}-\dfrac{1}{3}\sqrt{25\times 3}\\ \\&=&\dfrac{30}{3}\sqrt{3}-\dfrac{48}{5}\sqrt{3}+\dfrac{27}{2}\sqrt{3}-\dfrac{5}{3}\sqrt{3}\\ \\&=& \dfrac{300}{30}\sqrt{3}-\dfrac{288}{30}\sqrt{3}+\dfrac{405}{30}\sqrt{3}-\dfrac{50}{30}\sqrt{3}\\ \\&=&\dfrac{367}{30}\sqrt{3}\end{array}$
D'où, $$\boxed{B=\dfrac{367}{30}\sqrt{3}}$$
Exemple 2 :
Ecrivons les expressions suivantes sous la forme $a+b\sqrt{c}$ avec $a\in\mathbb{Q}\;,\ b\in\mathbb{Q}$ et $c\in\mathbb{Q}$
$\begin{array}{rcl} A&=&2\sqrt{3}(4-3\sqrt{3})\\ \\&=&8\sqrt{3}-18\end{array}$
D'où, $$\boxed{A=8\sqrt{3}-18}$$
$\begin{array}{rcl} B&=&3\sqrt{2}(3\sqrt{6}-2\sqrt{2})\\ \\&=&9\sqrt{12}-12\\ \\&=&9\sqrt{4\times 3}-12\\ \\&=&18\sqrt{3}-12\end{array}$
Donc, $$\boxed{B=18\sqrt{3}-12}$$
$\begin{array}{rcl} C&=&(2\sqrt{5}-3)^{2}\\ \\&=&20-12\sqrt{5}+9\\ \\&=&29-12\sqrt{5}\end{array}$
D'où, $$\boxed{C=29-12\sqrt{5}}$$
$\begin{array}{rcl} D&=&(\sqrt{2}+1)(\sqrt{2}+3)\\ \\&=&2+3\sqrt{2}+\sqrt{2}+3\\ \\&=&5+4\sqrt{2}\end{array}$
D'où, $$\boxed{D=5+4\sqrt{2}}$$
$\begin{array}{rcl} E&=&(2+\sqrt{5})^{2}\\ \\&=&4+4\sqrt{5}+5\\ \\&=&9+4\sqrt{5}\end{array}$
Donc, $$\boxed{E=9+4\sqrt{5}}$$
$\begin{array}{rcl} F&=&(\sqrt{5}-\sqrt{7})(\sqrt{5}+\sqrt{7})\\ \\&=&5-7\\ \\&=&-2\end{array}$
D'où, $$\boxed{F=-2}$$
II. Rendre rationnel le dénominateur d'un quotient : Expression conjuguée
II.1 Expression de la forme $\dfrac{N}{a\sqrt{b}}$ avec $a\in\mathbb{Q}^{*}$ et $b\in\mathbb{N}^{*}$
Règles :
Pour rendre rationnel le dénominateur d'une expression de la forme $\dfrac{N}{a\sqrt{b}}$, on multiplie tout simplement les termes du quotient par $\sqrt{b}.$
On a : $$\dfrac{N}{a\sqrt{b}}=\dfrac{N\times\sqrt{b}}{a\sqrt{b}\times\sqrt{b}}=\dfrac{N\sqrt{b}}{a.b}$$
Exemple 1 :
Rendons rationnel le dénominateur des expressions suivantes
$\begin{array}{rcl} A&=&\dfrac{5}{2\sqrt{3}}\\ \\&=&\dfrac{5\sqrt{3}}{2\sqrt{3}\times\sqrt{3}}\\ \\&=&\dfrac{5\sqrt{3}}{6}\end{array}$
Donc, $$\boxed{A=\dfrac{5\sqrt{3}}{6}}$$
$\begin{array}{rcl} B&=&\dfrac{2-2\sqrt{3}}{\sqrt{2}}\\ \\&=&\dfrac{(2-2\sqrt{3})\sqrt{2}}{\sqrt{2}\times\sqrt{2}}\\ \\&=&\dfrac{2\sqrt{2}-2\sqrt{6}}{2}\end{array}$
D'où, $$\boxed{B=\dfrac{2\sqrt{2}-2\sqrt{6}}{2}}$$
$\begin{array}{rcl} C&=&\dfrac{2\sqrt{3}}{3\sqrt{2}}\\ \\&=&\dfrac{2\sqrt{3}\times\sqrt{2}}{3\sqrt{2}\times\sqrt{2}}\\ \\&=&\dfrac{2\sqrt{6}}{6}\\ \\&=& \dfrac{\sqrt{6}}{3}\end{array}$
Donc, $$\boxed{C=\dfrac{\sqrt{6}}{3}}$$
Exemple 2 :
Ecrivons les expressions suivantes sous la forme $a\sqrt{b}$ avec $a\in\mathbb{Q}$ et $b\in\mathbb{N}$
$\begin{array}{rcl} A&=&\dfrac{2\sqrt{3}}{3\sqrt{2}} \\ \\&=&5\sqrt{\dfrac{27}{8}}-4\sqrt{\dfrac{15}{10}}-7\sqrt{\dfrac{48}{98}} \\ \\&=&5\sqrt{\dfrac{9\times 3}{4\times 2}}-4\sqrt{\dfrac{5\times 3}{5\times 2}}-7\sqrt{\dfrac{2\times 24}{2\times 49}} \\ \\&=&\dfrac{15\sqrt{3}}{2\sqrt{2}}-4\dfrac{\sqrt{3}}{\sqrt{2}}-7\sqrt{\dfrac{24}{49}} \\ \\ &=&\dfrac{15\sqrt{3}}{2\sqrt{2}}-4\dfrac{\sqrt{3}}{\sqrt{2}}-7\dfrac{\sqrt{4\times 6}}{\sqrt{49}} \\ \\&=&\dfrac{15\sqrt{6}}{4}-4\dfrac{\sqrt{6}}{2}-2\sqrt{6} \\ \\&=&\dfrac{15\sqrt{6}}{4}-8\dfrac{\sqrt{6}}{4}-8\dfrac{\sqrt{6}}{4} \\ \\&=&-\dfrac{\sqrt{6}}{4}\end{array}$
D'où, $$\boxed{A=-\dfrac{\sqrt{6}}{4}}$$
$\begin{array}{rcl} B&=&\dfrac{2}{3}\sqrt{\dfrac{54}{16}}-\dfrac{6}{5}\sqrt{\dfrac{3}{2}}-\dfrac{6}{18}\sqrt{6} \\ \\&=&\dfrac{2}{3}\dfrac{\sqrt{9\times 6}}{\sqrt{4\times 4}}-\dfrac{6}{5}\dfrac{\sqrt{3}}{\sqrt{2}}-\dfrac{6\sqrt{6}}{18} \\ \\&=&\dfrac{6\sqrt{6}}{12}-\dfrac{6\sqrt{6}}{10}-\dfrac{\sqrt{6}}{3} \\ \\&=&\dfrac{15\sqrt{6}}{30}-\dfrac{18\sqrt{6}}{30}-\dfrac{10\sqrt{6}}{30} \\ \\&=&-\dfrac{13\sqrt{6}}{30}\end{array}$
D'où, $$\boxed{B=-\dfrac{13\sqrt{6}}{30}}$$
II.2 Expression de la forme $\dfrac{N}{d(a+b\sqrt{c})}$ avec $a\;,\ b\;,\ d\;\in\mathbb{Q}^{*}$ et $c\in\mathbb{N}$
Règles :
Pour rendre rationnel le dénominateur d'une expression de la forme $\dfrac{N}{d(a+b\sqrt{c})}$, on multiplie tout simplement les termes du quotient par $(a-b\sqrt{c})$, appelé expression conjuguée de $(a+b\sqrt{c}).$
Remarque :
Cas où l'expression est de la forme $\dfrac{N}{a\sqrt{b}+c\sqrt{d}}$
Pour rendre rationnel le dénominateur d'une expression de la forme $\dfrac{N}{a\sqrt{b}+c\sqrt{d}}$, on multiplie les termes du quotient par $(a\sqrt{b}-c\sqrt{d})$, appelé expression conjuguée de l'expression $(a\sqrt{b}+c\sqrt{d}).$
Ainsi,
\begin{eqnarray}\dfrac{N}{d(a+b\sqrt{c})} & = & \dfrac{N\times (a-b\sqrt{c})}{d(a+b\sqrt{c})(a-b\sqrt{c})} \nonumber\\ \\ & = & \dfrac{N(a-b\sqrt{c})}{d(a^{2}-b^{2}.c)} \nonumber\end{eqnarray}
\begin{eqnarray}\dfrac{N}{a\sqrt{b}+c\sqrt{d})} & = & \dfrac{N\times (a\sqrt{b}-c\sqrt{d})}{a\sqrt{b}+c\sqrt{d})(a\sqrt{b}-c\sqrt{d})} \nonumber\\ \\ & = & \dfrac{N(a\sqrt{b}-c\sqrt{d})}{a^{2}.b-c^{2}.d} \nonumber\end{eqnarray}
Exemple 1 :
Rendons rationnel le dénominateur des expressions suivantes
$\begin{array}{rcl} A&=&\dfrac{2-3\sqrt{3}}{3+2\sqrt{3}} \\ \\&=&\dfrac{(2-3\sqrt{3})(3-2\sqrt{3})}{(3+2\sqrt{3})(3-2\sqrt{3})} \\ \\&=&\dfrac{6-4\sqrt{3}-9\sqrt{3}+12}{9-12} \\ \\&=&\dfrac{24-13\sqrt{3}}{-3} \\ \\&=&\dfrac{-24+13\sqrt{3}}{3} \\ \\&=&-8+\dfrac{13\sqrt{3}}{3}\end{array}$
D'où, $$\boxed{A=-8+\dfrac{13\sqrt{3}}{3}}$$
$\begin{array}{rcl} B&=&\dfrac{2\sqrt{2}}{-3(-3+2\sqrt{2})} \\ \\&=&\dfrac{2\sqrt{2}(-3-2\sqrt{2})}{-3(-3+2\sqrt{2})(-3-2\sqrt{2})} \\ \\&=&\dfrac{-6\sqrt{2}-8}{-3(9-8)} \\ \\&=&\dfrac{-6\sqrt{2}-8}{-3} \\ \\&=&\dfrac{6\sqrt{2}+8}{3}\end{array}$
Donc, $$\boxed{B=\dfrac{6\sqrt{2}+8}{3}}$$
$\begin{array}{rcl} C&=&\dfrac{2\sqrt{2}-3\sqrt{3}}{4\sqrt{3}+5\sqrt{2}} \\ \\&=&\dfrac{(2\sqrt{2}-3\sqrt{3})(4\sqrt{3}-5\sqrt{2})}{(4\sqrt{3}+5\sqrt{2})(4\sqrt{3}-5\sqrt{2})} \\ \\&=&\dfrac{8\sqrt{6}-20-36+15\sqrt{6}}{48-50} \\ \\&=&\dfrac{-56+23\sqrt{6}}{-2} \\ \\&=&\dfrac{56-23\sqrt{6}}{2} \\ \\&=&28-\dfrac{23\sqrt{6}}{2}\end{array}$
D'où, $$\boxed{C=28-\dfrac{23\sqrt{6}}{2}}$$
Exemple 2 :
Ecrivons l'expression suivante sous la forme $a+b\sqrt{c}$ avec $a\;,\ b\;\in\mathbb{Q}$ et $c\in\mathbb{N}$
$\begin{array}{rcl} A=\dfrac{\left(\dfrac{-4+2\sqrt{5}}{3\sqrt{5}-1}\right)}{\left(\dfrac{2\sqrt{5}-1}{-\sqrt{5}-3}\right)}&=&\dfrac{-4+2\sqrt{5}}{3\sqrt{5}-1}\times\dfrac{-\sqrt{5}-3}{2\sqrt{5}-1} \\ \\ & = & \dfrac{4\sqrt{5}+12-10-6\sqrt{5}}{45-6\sqrt{5}+1} \\ \\&=&\dfrac{2-2\sqrt{5}}{46-6\sqrt{5}} \\ \\&=&\dfrac{1-\sqrt{5}}{23-3\sqrt{5}} \\ \\&=&\dfrac{(1-\sqrt{5})(23+3\sqrt{5})}{(23-3\sqrt{5})(23+3\sqrt{5})} \\ \\&=&\dfrac{23+3\sqrt{5}-23\sqrt{5}-15}{529-45} \\ \\&=&\dfrac{8-20\sqrt{5}}{484} \\ \\&=&\dfrac{2-5\sqrt{5}}{121}\end{array}$
D'où, $$\boxed{A=\dfrac{2-5\sqrt{5}}{121}}$$
III. Comparaison de réels comportant des radicaux
III.1 Réels du type $a\sqrt{b}$
Règle 1 :
Pour comparer deux réels positifs du type $a\sqrt{b}$ on les élève au carré et celui qui aura le carré le plus grand correspondra au réel le plus grand.
Exemple 1 :
Comparons les réels suivants
$3\sqrt{2}$ et $2\sqrt{3}$ puis, $5$ et $2\sqrt{7}.$
On a : $(3\sqrt{2})^{2}=18$ et $(2\sqrt{3})^{2}=12$
Or, $18>12$ alors, $3\sqrt{2}>2\sqrt{3}.$
De même on a $(5)^{2}=25$ et $(2\sqrt{7})^{2}=28$
Or, $28>25$ alors, $2\sqrt{7}>5.$
Exemple 2 :
Trouvons le signe des expressions suivantes
$3-2\sqrt{5}$ puis $-5+2\sqrt{7}$
On a : $(3)^{2}=9$ et $(2\sqrt{7})^{2}=28$
Or, $9<28$ alors, $3<2\sqrt{7}$
Donc, $3-2\sqrt{5}<0$
De même on a $(5)^{2}=25$ et $(2\sqrt{7})^{2}=28$
Or, $28>25$ alors, $2\sqrt{7}>5$
Donc, $-5+2\sqrt{7}>0$
Règle 2 :
Pour comparer deux réels négatifs du type $a\sqrt{b}$ on les élève au carré et celui qui aura le carré le plus petit correspondra au réel le plus grand.
Exemple 1 :
Comparons les réels suivants
$-3\sqrt{2}$ et $-2\sqrt{3}$ puis, $-4$ et $-2\sqrt{5}.$
On a : $(-3\sqrt{2})^{2}=18$ et $(-2\sqrt{3})^{2}=12$
Or, $12<18$ alors, $-3\sqrt{2}<-2\sqrt{3}.$
De même on a $(-4)^{2}=16$ et $(-2\sqrt{5})^{2}=20$
Or, $16<20$ alors, $-4>-2\sqrt{5}.$
Exemple 2 :
Trouvons deux entiers relatifs consécutifs qui encadrent $-2\sqrt{3}$
On a : $(-2\sqrt{3})^{2}=12$ ; or 9<12<16 et $-2\sqrt{3}<0$ alors, $(-3)^{2}<(-2\sqrt{3})^{2}<(-4)^{2}$
Donc, $-4<-2\sqrt{3}<-3$
III.2 Réels du type $a+b\sqrt{c}$ et $\sqrt{a'+b'\sqrt{c}}$
Exemple :
Comparons les réels suivants
$2-\sqrt{2}$ et $\sqrt{6-4\sqrt{2}}$
signe de $2-\sqrt{2}$ : on a $(2)^{2}=4$ et $(\sqrt{2})^{2}=2$ alors, $2>\sqrt{2}.$
Donc, $2-\sqrt{2}>0$
Ainsi, $(2-\sqrt{2})^{2}=4-4\sqrt{2}+2=6-4\sqrt{2}$ et $\left(\sqrt{6-4\sqrt{2}}\right)^{2}=6-4\sqrt{2}$
Par suite, $2-\sqrt{2}=\sqrt{6-4\sqrt{2}}$
IV Racine carrée du carré d'un réel
IV.1 Rappels : valeur absolue d'un réel
IV.1.1 Définition :
On appelle valeur absolue d'un nombre réel $a$, notée $|a|$, le réel positif défini de la manière suivante :
$$|a|=a\;\text{ si, et seulement si, }\;a\geq 0$$
$$|a|=-a\;\text{ si, et seulement si, }\;a<0$$
Remarque :
La valeur absolue d'un nombre réel est toujours positif.
Exemple :
On a :
$|2.21|=2.21\;,\ \left|-\dfrac{3}{7}\right|=\dfrac{3}{7}\;,\ |-2\sqrt{3}|=2\sqrt{3}$
$|3+\sqrt{2}|=3+\sqrt{2}\;,\ |3-\sqrt{2}|=3-\sqrt{2}$
$|2\sqrt{3}-4|=-(2\sqrt{3}-4)=-2\sqrt{3}+4$
IV.1.2 Propriétés
$P_{1}\ :\ $ Soient $x\in\mathbb{R}$ et $y\in\mathbb{R}^{+}$
On a : $|x|=y$ si, et seulement si $x=y$ ou $x=-y$
Exemple :
Résolvons les équations suivantes
$\centerdot\ \ |2x+3|=5$
On aura $2x+3=5$ ou $2x+3=-5$
Alors, $2x=2$ ou $2x=-8$
Donc, $x=1$ ou $x=-4$
D'où, $$S=\{-4\;;\ 1\}$$
$\centerdot\ \ \left|-\dfrac{2}{3}x+4\right|=6$
On aura $-\dfrac{2}{3}x+4=6$ ou $-\dfrac{2}{3}x+4=-6$
Alors, $-\dfrac{2}{3}x=2$ ou $-\dfrac{2}{3}x=-10$
Donc, $x=2\left(-\dfrac{3}{2}\right)=-3$ ou $x=-10\left(-\dfrac{3}{2}\right)=15$
D'où, $$S=\{-3\;;\ 15\}$$
$P_{2}\ :\ $ Soient $x\in\mathbb{R}$ et $y\in\mathbb{R}$
On a : $|x|=|y|$ si, et seulement si, $x=y$ ou $x=-y$
Exemple :
Résolvons les équations suivantes
$\centerdot\ \ |3x+5|=|2x+7|$
On aura $3x+5=2x+7$ ou $3x+5=-2x-7$
Alors, $x=2$ ou $5x=-12$
Donc, $x=2$ ou $x=-\dfrac{12}{5}$
D'où, $$S=\left\lbrace-\dfrac{12}{5}\;;\ 1\right\rbrace$$
$\centerdot\ \ \left|\dfrac{2}{3}x+3\right|=\left|-\dfrac{3}{2}x+5\right|$
On aura $\dfrac{2}{3}x+3=-\dfrac{3}{2}x+5$ ou $\dfrac{2}{3}x+3=\dfrac{3}{2}x-5$
Alors, $\dfrac{2}{3}x+\dfrac{3}{2}x=2$ ou $\dfrac{2}{3}x-\dfrac{3}{2}x=-8$
Donc, $\dfrac{4}{6}x+\dfrac{9}{6}x=2$ ou $\dfrac{4}{6}x-\dfrac{9}{6}x=-8$
Ainsi, $\dfrac{13}{6}x=2$ ou $\dfrac{5}{6}x=-8$
Par suite, $x=2\left(\dfrac{6}{13}\right)=\dfrac{12}{13}$ ou $x=-8\left(-\dfrac{6}{5}\right)=\dfrac{48}{5}$
D'où, $$S=\left\lbrace\dfrac{12}{13}\;;\ \dfrac{48}{5}\right\rbrace$$
$P_{3}\ :\ $ Soient $x\in\mathbb{R}$ et $y\in\mathbb{R}^{+}$
On a : $|x|\leq y$ si, et seulement si $x\leq y$ et $x\geq -y$
Exemple :
Résolvons les inéquations suivantes
$\centerdot\ \ |3x+7|\leq 5$
On aura : $3x+7\leq 5$ et $3x+5\geq -5$
Alors, $3x\leq -2$ et $3x\geq -12$
Donc, $x\leq -\dfrac{2}{3}$ et $x\geq -4$
D'où $$S=\left[-4\;;\ -\dfrac{2}{3}\right]$$
$\centerdot\ \ \left|-\dfrac{2}{3}x+4\right|< 6$
On aura : $-\dfrac{2}{3}x+4< 6$ et $-\dfrac{2}{3}x+4> -6$
Alors, $-\dfrac{2}{3}x< 2$ et $-\dfrac{2}{3}x>-10$
Donc, $x>6\left(-\dfrac{3}{2}\right)$ et $x< -10\left(-\dfrac{3}{2}\right)$
Ainsi, $x>-3$ et $x<15$
D'où, $$S=\left]-3\;;\ 15\right[$$
$P_{4}\ :\ $ Soient $x\in\mathbb{R}$ et $y\in\mathbb{R}^{+}$
On a : $|x|\geq y$ si, et seulement si $x\geq y$ ou $x\leq -y$
Exemple :
Résolvons les inéquations suivantes
$\centerdot\ \ |2x-5|\geq 7$
On aura : $2x-5\geq 7$ ou $2x-5\leq -7$
Alors, $2x\geq 12$ ou $2x\leq -2$
Donc, $x\geq 6$ ou $x\leq -1$
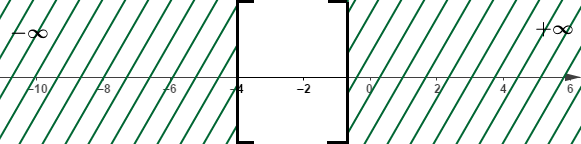
D'où $$S=]-\infty\;;\ -1]\cup[6\;;\ +\infty[$$
$\centerdot\ \ \left|-\dfrac{3}{2}x+6\right|>9$
On aura : $-\dfrac{3}{2}x+6>9$ ou $-\dfrac{3}{2}x+6<-9$
Alors, $-\dfrac{3}{2}x>3$ ou $-\dfrac{3}{2}x<-15$
Donc, $x<3\left(-\dfrac{2}{3}\right)$ ou $x>-15\left(-\dfrac{2}{3}\right)$
Ainsi, $x<-2$ ou $x>10$
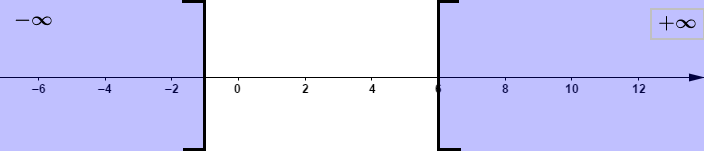
$$S=]-\infty\;;\ -2[\cup]10\;;\ +\infty[$$
IV.2 Expression de la racine carrée du carré d'un réel en fonction de la valeur absolue du réel
On a ; pour $x\geq 0\;;\ \sqrt{x^{2}}=x$ et pour $x<0\;;\ \sqrt{x^{2}}=-x.$
Et comme pour $x\geq 0\;;\ |x|=x$ et pour $x<0\;;\ |x|=-x.$
Ainsi, $|x|=\sqrt{x^{2}}$
$$\text{Pour }\;x\in\mathbb{R}\;;\ \text{ on a }\;\ \sqrt{x^{2}}=|x|$$
Applications
1) On donne $A=2\sqrt{3}-4$ et $B=\sqrt{28-16\sqrt{3}}$
Calculer $A^{2}$ puis en déduire une écriture simplifiée de $B.$
On a : $A^{2}=(2\sqrt{3}-4)^{2}=12-16\sqrt{3}+16=28-16\sqrt{3}$
Alors, $B=\sqrt{28-16\sqrt{3}}=\sqrt{A^{2}}=|A|.$
Donc, $B=|2\sqrt{3}-4|$
signe de $2\sqrt{3}-4$ : on a $(2\sqrt{3})^{2}=12$ et $(4)^{2}=16$. Alors, $2\sqrt{3}-4<0.$
Ainsi, $B=-2\sqrt{3}+4$
2) Résoudre l'équation suivante :
$4x^{2}-9=0$
On aura : $4x^{2}=9$
Alors, $x^{2}=\dfrac{9}{4}$
Donc, $\sqrt{x^{2}}=\sqrt{\dfrac{9}{4}}$
Par suite $|x|=\dfrac{3}{2}$
Ainsi, $x=\dfrac{3}{2}$ ou $x=-\dfrac{3}{2}$
D'où, $$S=\left\lbrace -\dfrac{3}{2}\;;\ \dfrac{3}{2}\right\rbrace$$
3) Résoudre l'inéquation suivante :
$16x^{2}-25\leq 0$
On aura : $16x^{2}\leq 25$
Alors, $x^{2}\leq\dfrac{25}{16}$, donc $\sqrt{x^{2}}\leq\sqrt{\dfrac{25}{16}}.$
Ainsi, $|x|\leq\dfrac{5}{4}$
Par suite, $x\leq\dfrac{5}{4}$ et $x\geq\dfrac{-5}{4}$
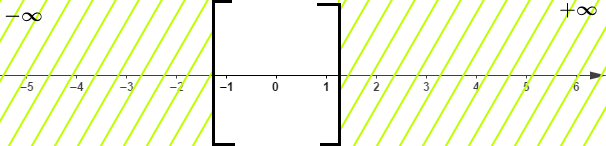
D'où $$S=\left[-\dfrac{5}{4}\;;\ \dfrac{5}{4}\right]$$
V. Valeur approchée - encadrement
V.1 Valeur approchée
$3$ n'étant pas un carré parfait, il nous est alors impossible de donner la valeur exacte de $\sqrt{3}.$
Mais pour $k\in\mathbb{N}$, on peut trouver une valeur approchée par défaut ou par excès de $\sqrt{3}$ à $10^{-k}$ près ($k$ chiffres après la virgule).
Exemple 1 :
Trouver la valeur approchée par défaut de $\sqrt{3}$ à $10^{-1}$ près.
Je cherche deux entiers consécutifs tels que , $a.10^{-1}<\sqrt{3}<(a+1).10^{-1}.$
J'élève l'inégalité au carré. On obtient $a^{2}.10^{-2}<3<(a+1)^{2}.10^{-2}.$
Je multiplie par $10^{+2}$ pour faire disparaitre les $10^{-2}.$ On trouve $a^{2}<300<(a+1)^{2}.$
Je cherche maintenant deux carrés parfaits consécutifs qui encadrent $300.$
On a : $289<300<324$, c'est à dire $17^{2}<300<(17+1)^{2}.$
J'en déduis alors que $a=17\;,\ a+1=18$ et $a.10^{-1}=1.7$
Je reviens à la condition posée au départ, $1.7<\sqrt{3}<1.8$
$1.7$ est la valeur approchée par défaut de $\sqrt{3}$ à $10^{-1}$ près.
$1.8$ est la valeur approchée par excès de $\sqrt{3}$ à $10^{-1}$ près.
Exemple 2 :
Donner l'encadrement de $\sqrt{2}$ à $10^{-3}$ près.
Soit $a\in\mathbb{N}$
On aura : $a.10^{-3}<\sqrt{2}<(a+1).10^{-3}.$
Alors, $a^{2}.10^{-6}<2<(a+1)^{2}.10^{-6}.$
Donc, $a^{2}<2.000.000<(a+1)^{2}.$
Ainsi, $a=1414$ et $a.10^{-3}=1.414$, d'où $1.414<\sqrt{2}<1.415$
V.2 Encadrement de réels comportant des radicaux
Exemple 1 :
Sachant que $1.732<\sqrt{3}<1.733$ donner un encadrement de $2\sqrt{3}-4$ à $10^{-2}$ près.
On a : $1.732<\sqrt{3}<1.733$
Alors, $3.464<2\sqrt{3}<3.466$
Donc, $-0.536<2\sqrt{3}-4<-0.534$
D'où, $-0.54<2\sqrt{3}-4<-0.53$
Exemple 2 :
Sachant que $2.236<\sqrt{5}<2.237$ donnons un encadrement de $\dfrac{5-2\sqrt{5}}{2}$ à $10^{-2}$ près.
On a : $2.236<\sqrt{5}<2.237$
Alors, $-4.472>-2\sqrt{5}>-4.474$
Donc, $0.528>5-2\sqrt{5}>0.526$
Ainsi, $0.264>\dfrac{5-2\sqrt{5}}{2}>0.263$
Par suite, $0.263<\dfrac{5-2\sqrt{5}}{2}<0.264$, d'où $0.26<\dfrac{5-2\sqrt{5}}{2}<0.27$



Commentaires
Moctar greve (non vérifié)
mer, 09/25/2019 - 23:51
Permalien
Machalah
Moctar greve (non vérifié)
mer, 09/25/2019 - 23:51
Permalien
Machalah
babacar diagne (non vérifié)
mar, 10/01/2019 - 23:36
Permalien
je suis trés content pour ce
Anonyme (non vérifié)
jeu, 10/24/2019 - 19:15
Permalien
Très intéressant
MODOU SARR (non vérifié)
mar, 12/17/2019 - 16:48
Permalien
très bon cours
Anonyme (non vérifié)
mar, 01/14/2020 - 22:57
Permalien
J'aime vraiment
Papa Dieng (non vérifié)
mar, 01/14/2020 - 23:02
Permalien
J'aime vraiment
Bouchaib (non vérifié)
sam, 08/29/2020 - 11:01
Permalien
Bravo pour le grand effort
Anonyme (non vérifié)
mer, 09/09/2020 - 18:20
Permalien
Bien!!
Anonyme (non vérifié)
ven, 09/18/2020 - 14:01
Permalien
Les cours sont excellents,je
Anonyme (non vérifié)
jeu, 10/29/2020 - 11:42
Permalien
Nous vous remercions
Mohamed NDOUR (non vérifié)
lun, 11/30/2020 - 22:11
Permalien
Bonjour, je voulais signalé
Seynabou(non vé... (non vérifié)
mer, 12/09/2020 - 22:55
Permalien
je suis très content pour
Ismaïla Siby (non vérifié)
mar, 01/12/2021 - 21:47
Permalien
Très fort
Ismaïla Siby (non vérifié)
mar, 01/12/2021 - 21:48
Permalien
Très fort
Ismaïla Siby (non vérifié)
mar, 01/12/2021 - 21:48
Permalien
C'EST trop bien
Ismaïla Siby (non vérifié)
mar, 01/12/2021 - 21:50
Permalien
C'est super merci beaucoup
Anonyme (non vérifié)
jeu, 03/04/2021 - 16:09
Permalien
je valide
Fatou gueye (non vérifié)
dim, 04/25/2021 - 15:21
Permalien
Merci du courage
Cherif sow (non vérifié)
mar, 04/27/2021 - 17:50
Permalien
Je vous remercie parfaitement
Al moustapha (non vérifié)
lun, 08/02/2021 - 18:08
Permalien
Très intéressant
Anonyme (non vérifié)
lun, 08/02/2021 - 18:16
Permalien
Intéressant
Abdoulaye sy (non vérifié)
lun, 09/13/2021 - 02:47
Permalien
Constat d’une erreur de saisie sur l’inégalité d’une valeur abso
Cheikhou Kanté (non vérifié)
mer, 11/03/2021 - 12:37
Permalien
Les cours sont claires et
Anonyme (non vérifié)
mar, 01/11/2022 - 20:49
Permalien
C'est bien.
Ndéné Ndiaye (non vérifié)
mer, 08/17/2022 - 09:00
Permalien
Excellent cours
Mouhamed Habib ... (non vérifié)
dim, 10/22/2023 - 17:19
Permalien
Vous êtes imparfait mais
Philo (non vérifié)
ven, 01/26/2024 - 10:33
Permalien
Les cours sont bien détaillés
Ajouter un commentaire