Relations trigonométriques dans un triangle rectangle 3e
Classe:
Troisième
I. Projection orthogonale
1) Définition - construction
Soit (Δ) une droite donnée et A un point du plan n'appartenant pas à (Δ).
Construisons (Δ′), la droite passant par A et perpendiculaire à (Δ).
Et soit H le point d'intersection de (Δ) et (Δ′).
H est appelé projeté orthogonal de A sur (Δ).
On dit aussi que H est le pied de la perpendiculaire à (Δ), issue de A.
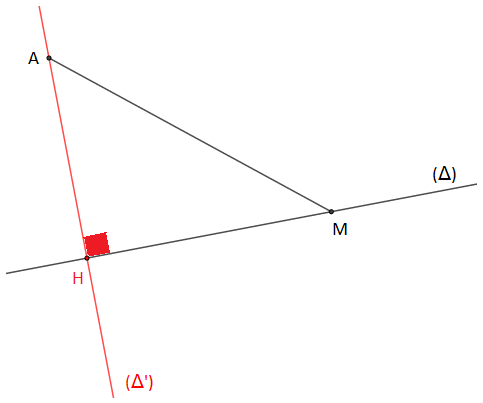
Soit M un point quelconque de (Δ) tel que M≠H, alors on a : AH<AM
La distance AH est donc inférieure aux distances AM pour tous les points M appartenant à (Δ) autres que H.
2) Propriété
Soient (Δ) et (Δ′) deux droites sécantes en O.
A et B deux points distincts de (Δ); A′ et B′ les projetés orthogonaux respectifs de A et B sur (Δ′), alors on a : A′B′<AB
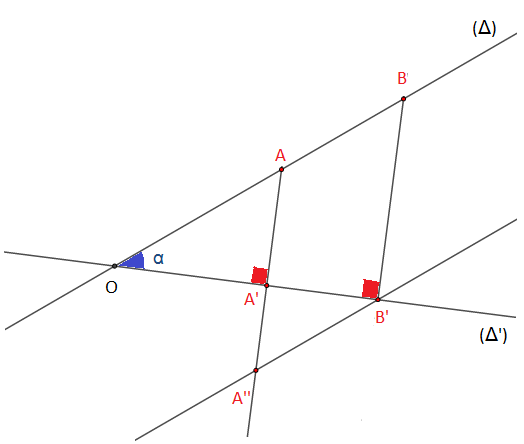
Soit A″ le point d'intersection de (AA′) à la parallèle à (AB) passant par B′.
On aura ABB′B″ un parallélogramme, alors AB=A″B′.
Et comme A′B′<A″B′, donc A′B′<AB
3) Rapport de projection orthogonale
a) Activité
Soient [Ox) et [Oy) deux demi-droites de même origine O et de supports non parallèles tels que ^xOy=60∘.
Soient A, B et C trois points de [Oy) tels que OA=5cm, OB=8cm et OC=10cm.
A′, B′ et C′ sont les projetés orthogonaux respectivement de A, B et C sur [Ox).
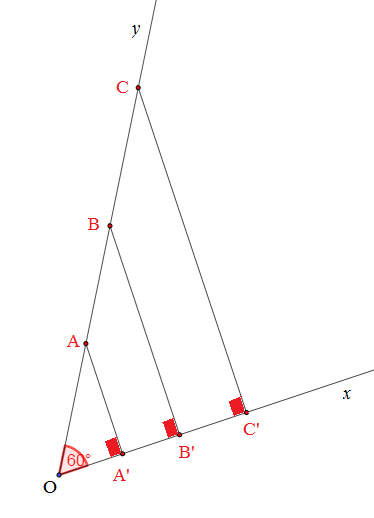
On a : OA′=2.5cm, OB′=4cm et OC′=5cm.
Alors, OA′OA=2.55=12, OB′OB=48=12 et OC′OC=510=12.
A′B′AB=1.53=12 et A′C′AC=2.55=12
Donc, OA′OA=OB′OB=OC′OC=A′B′AB=A′C′AC=12
b) Définition
Soient (Δ) et (Δ′) deux droites non parallèles, A et B deux points de (Δ), A′, B′ leur projetés orthogonaux respectifs sur la droite (Δ′).
On appelle rapport de projeté orthogonal sur la droite (Δ′) à la droite (Δ) le rapport A′B′AB.
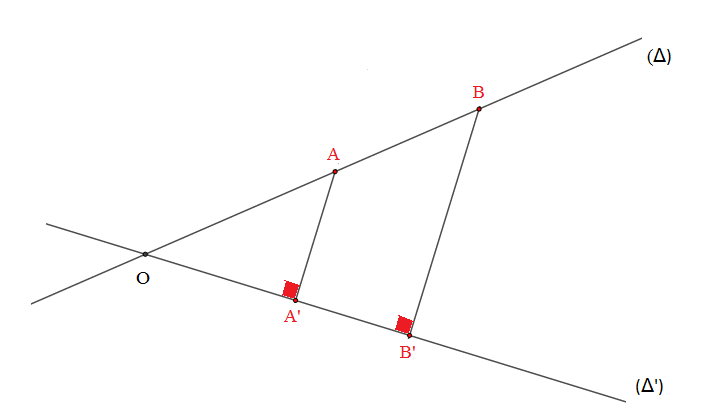
Si on désigne par r ce rapport de projection orthogonale de (Δ) sur (Δ′).
On écrira : r=OA′OA=OB′OB=A′B′AB
Remarque :
Le rapport de projection orthogonale de la droite (Δ) sur la droite (Δ′) est indépendant de la position de A et B sur (Δ) mais dépend uniquement de l'angle formé par les deux droites.
c) Propriétés :
Le rapport de projection orthogonale de la droite (Δ) sur la droite (Δ′) est égal au rapport de projection de la droite (Δ′) sur la droite (Δ).
On dira que le rapport de projection orthogonale est symétrique.
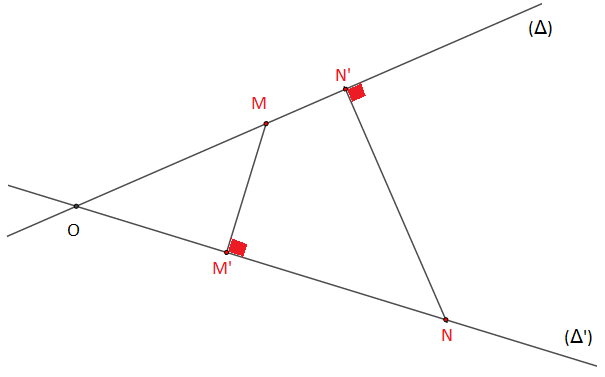
r=OM′OM=ON′ON
d) Valeurs du rapport
Soit r le rapport de projection orthogonale des droites (Δ) et (Δ′).
⋅ (Δ) et (Δ′) sécantes en O
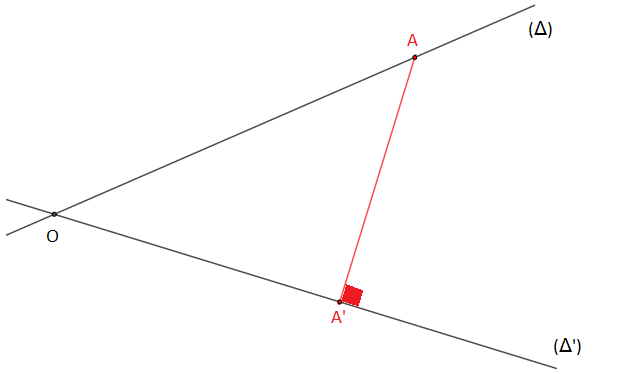
On a : OA′<OA
Alors, OA′OA<OAOA
Donc, r<1
Remarque :
Si (Δ)⊥(Δ′) alors, r=0
D'où, 0≤r<1
(Δ) et (Δ′) sont confondues
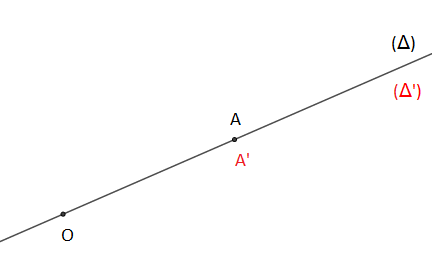
On a : r=OA′OA=OAOA=1
II. Relations trigonométriques dans un triangle rectangle
Rappel
Soit ABC un triangle rectangle en A, x et y les angles respectifs aux sommets B et C
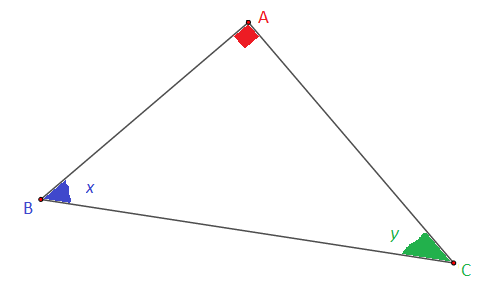
⋅ On a x<90∘ et y<90∘ et x+y=90∘.
Dans un triangle rectangle, on a deux angles aigus complémentaires.
⋅ Si ABC un triangle et ^ABC+^ACB=90∘ alors, ABC est un triangle rectangle en A.
Si dans un triangle, on a deux angles complémentaires alors, c'est un triangle rectangle.
⋅ Si ABC un triangle rectangle en A, alors BC>AB et BC>AC.
Dans un triangle rectangle le côté opposé à l'angle droit est le plus grand côté et il est appelé l'hypoténuse.
⋅ Si ABC un triangle rectangle en A alors, BC2=AB2+AC2.
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la mesure des carrés des deux autres côtés (théorème de Pythagore)
⋅ Si ABC un triangle rectangle et BC2=AB2+AC2 alors, ABC est rectangle en A.
Si dans un triangle, le carré d'un côté est égal à la somme des carrés des deux autres, alors c'est un triangle rectangle.
⋅ On appelle côté opposé à un angle aigu, le côté qui fait face à l'angle aigu dans le triangle rectangle.
[AB] et [AC] sont appelés côtés opposés aux angles respectifs y et x.
⋅ On appelle côté adjacent à un angle aigu dans un triangle rectangle, le côté qui porte l'angle dans le triangle autre que l'hypoténuse.
[AB] et [AC] sont appelés côtés adjacents aux angles respectifs x et y.
III. Cosinus d'un angle aigu
On appelle cosinus d'un angle aigu x, noté cosx, le rapport de la longueur du côté adjacent à l'ange x sur la longueur de l'hypoténuse.
On écrira : cosx=côté adjacent à xhypoténuse
Ainsi, cosx=ABBC et cosy=ACBC
Exemple 1 :
Soit ABC un triangle rectangle en A tel que AB=4cm et BC=5cm
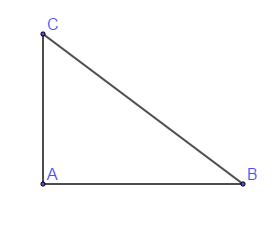
1) Calcul de AC
On a ABC triangle rectangle en A alors, AB2+AC2=BC2
Donc, AC2=BC2−AB2
Ainsi, AC=√BC2−AB2
D'où, AC=√25−16=3cm
2) Calcul de cos^ABC et cos^ACB
On a ABC triangle rectangle en A, alors cos^ABC=ABBC et cos^ACB=ACBC
Donc, cos^ABC=45 et cos^ACB=35
D'où, cos^ABC=0.8 et cos^ACB=0.6
Exemple 2 :
On considère la figure suivante
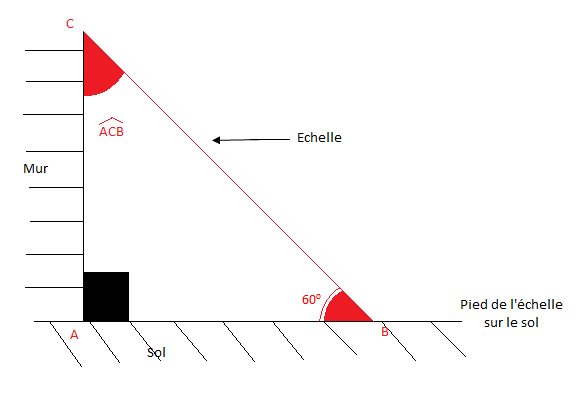
On donne AB=3m et cos60∘=12
1) Calcul de la longueur de l'échelle : BC
On a ABC triangle rectangle en A, alors cos^ABC=ABBC
Donc, BC=ABcos^ABC
Ainsi, BC=3cos60∘=312
D'où, BC=3×21=6m
2) Calcul de AC (hauteur du pied de l'échelle sur le mur au sol)
On a ABC triangle rectangle en A, alors AB2+AC2=BC2
Donc, AC2=BC2−AB2
Ainsi, AC=√BC2−AB2
D'où, AC=√36−9=√27=3√3m
3) Mesure de ^ACB
On a ABC un triangle rectangle en A
Alors, ^ABC+^ACB=90∘
Donc, ^ACB=90∘−^ABC
Ainsi, ^ACB=90∘−60∘
D'où, ^ACB=30∘
4) Calcul de cos^ACB
On a ABC triangle rectangle en A, alors cos^ACB=ACBC
Donc, cos^ACB=3√36
D'où, cos^ACB=√32
IV. Sinus d'un angle aigu
On appelle sinus d'un angle aigu x, noté sinx, le rapport de la longueur du côté opposé à l'ange x sur la longueur de l'hypoténuse.
On écrira : sinx=côté opposé à xhypoténuse
Ainsi, sinx=ACBC et siny=ABBC
V. Sinus et cosinus d'angles complémentaires
On avait sinx=ACBC et cosx=ABBC
siny=ABBC et cosy=ACBC
Alors, sinx=cosy et siny=cosx
Si deux angles sont complémentaires, le sinus de l'un est égal au cosinus de l'autre.
Si x+y=90∘, alors cosx=siny et cosy=sinx
VI. Relation entre sinus et cosinus d'un angle aigu
On a ABC un triangle rectangle en A
Alors, AB2+AC2=BC2
Donc, AB2BC2+AC2BC2=BC2BC2
c'est à dire (ABBC)2+(ACBC)2=1
Ainsi, (cosx)2+(sinx)2=1
en posant (cosx)2=cos2x et (sinx)2=sin2x
on obtient cos2x+sin2x=1
Exemple :
Soit ABC un triangle rectangle en A tel que AB=4cm
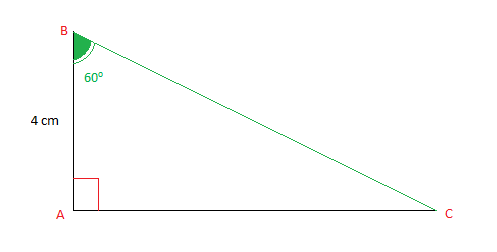
l'angle ^ABC=60∘ et sin60∘=√32
Calculons BC et AC
On a : cos2^ABC+sin2^ABC=1
Alors, cos2^ABC=1−sin2^ABC
Donc, cos^ABC=√1−sin2^ABC
Ainsi, cos^ABC=√1−(√32)2=√1−34=√14=12
Par suite, cos^ABC=ABBC
c'est à dire BC=ABcos^ABC=412=8cm
et sin^ABC=ACBC
Ce qui donne : AC=BC×sin^ABC
Donc, AC=8×√32=4√3cm
VII. Tangente d'un angle aigu
On appelle tangente d'un angle aigu x, notée tanx ou tgx, le rapport du sinus de l'angle x par son cosinus.
On écrira : tanx=sinxcosxettany=sinycosy
Autres formulations :
On a : tanx=sinxcosx
Or, sinx=ACBC et cosx=ABBC
Alors, tanx=ACBCABBC
Donc, tanx=ACBC×BCAB
D'où, tanx=ACAB
La tangente d'un angle aigu dans un triangle rectangle se définit comme étant le rapport de la longueur du côté opposé à l'angle par son côté adjacent.
On écrira : tanx=côté opposé à xcôté adjacent à x
Ainsi, tanx=ACAB et tany=ABAC
Remarque :
Si deux angles complémentaires, la tangente de l'une est égale à l'inverse de la tangente de l'autre.
Si x+y=90∘, alors tanx=1tany
VIII. Sinus, cosinus et tangente d'angles remarquables
Angle x0∘30∘45∘60∘90∘Sinus012√22√321Cosinus1√32√22120Tangente0√331√3×
XI. Applications : Relations métriques dans un triangle rectangle
Soit ABC un triangle rectangle en A, H le projeté orthogonal de A sur (BC).
On donne AB=4cm, AC=3cm et BC=5cm
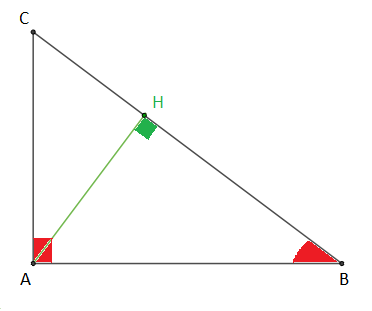
⋅ Exprimons cos^ABC de deux manières
On a ABC un triangle rectangle en A, alors cos^ABC=ABBC.
De même on a ABH un triangle rectangle en H, alors cos^ABH=BHAB
Or, ^ABH=^ABC
Donc, cos^ABC=BHAB
⋅ Relations entre AB, BC et BH
On a : cos^ABC=ABBC et cos^ABC=BHAB
Alors, ABBC=BHAB
Donc, AB2=BH×BC1erelation métrique
Valeur de BH
On a : AB2=BH×BC
Alors, BH=AB2BC
Donc, BH=165=3.2cm
⋅ Relations entre AC, BC et CH
On a ABC un triangle rectangle en A
Alors, cos^ACB=ACBC
De même on a ACH un triangle rectangle en H, alors cos^ACH=CHAC
Or, ^ACH=^ACB
Donc, cos^ACB=CHAC
Par suite, ACBC=CHAC
D'où, AC2=CH×BC2erelation métrique
Valeur de CH
On aura CH=AC2BC
Donc, BH=95=1.8cm
⋅ Relations entre AH, BH et CH
On a ABH un triangle rectangle en H, alors tan^ABH=AHBH
Or, ^ABH=^ABC
Donc, tan^ABC=AHBH
De même on a ACH un triangle rectangle en H, alors tan^ACH=AHCH
Or, ^ACH=^ACB
Donc, tan^ACB=AHCH
et comme ^ABC+^ACB=90∘, on aura tan^ABC=1tan^ACB
Par suite, AHBH=1AHCH
Ainsi, AHBH=CHAH
D'où, AH2=BH×CH3erelation métrique
Valeur de AH
On aura AH=√BH×CH
Donc, BH=√165×95=125=2.4cm
Auteur:
Abdoulaye Ba

Commentaires
Anonyme (non vérifié)
lun, 01/21/2019 - 21:01
Permalien
Bien
Kia (non vérifié)
mar, 01/14/2020 - 23:10
Permalien
Je vaudrait savoir plus sur la relation metrique
Kia (non vérifié)
mar, 01/14/2020 - 23:16
Permalien
Vaudrai
Anonyme (non vérifié)
sam, 05/23/2020 - 18:41
Permalien
VRAIMENT TRES INTERESSANT
Anonyme (non vérifié)
sam, 05/23/2020 - 18:41
Permalien
VRAIMENT TRÈS INTÉRESSANT
Oury diallo (non vérifié)
jeu, 02/25/2021 - 23:20
Permalien
Réussir mon bfem
Mamadou Diallo (non vérifié)
jeu, 01/19/2023 - 21:06
Permalien
Bonsoir les cours sont
Mamadou Diallo (non vérifié)
jeu, 01/19/2023 - 21:07
Permalien
Intéressant
Ajouter un commentaire