Solutions exercices : Calcul vectoriel - 2nd
Classe:
Seconde
Exercice 1
a)
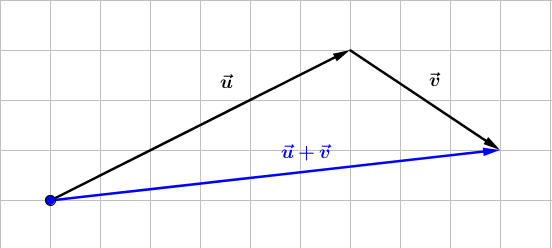

b) 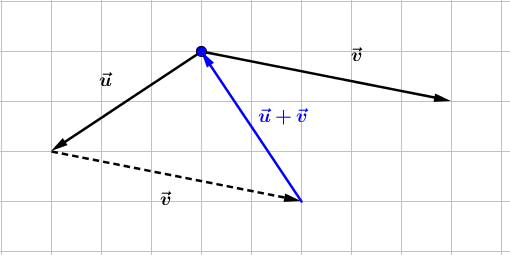
c)
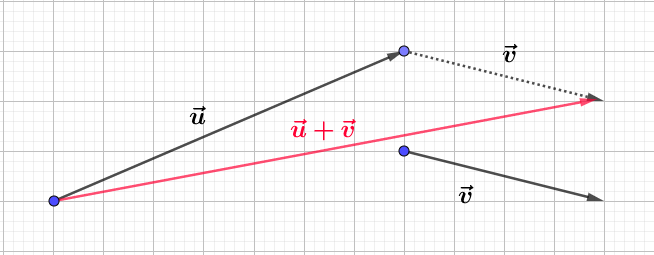
d)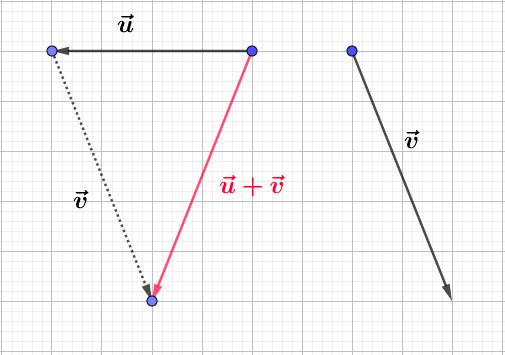
e)
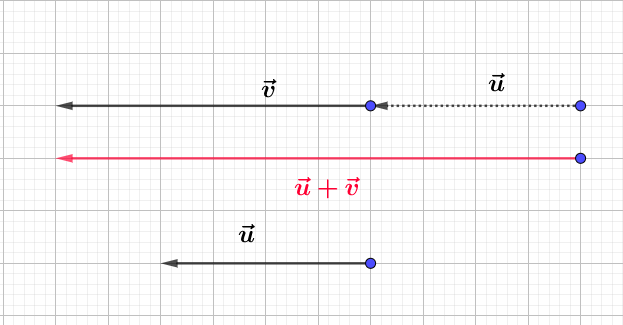
f)
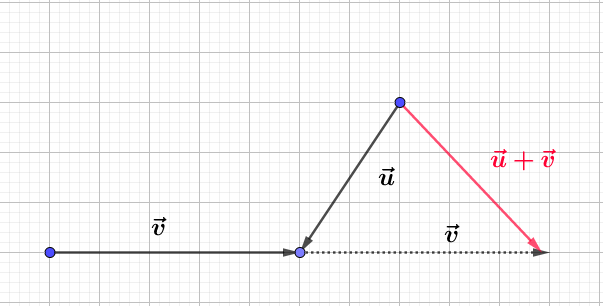
g)
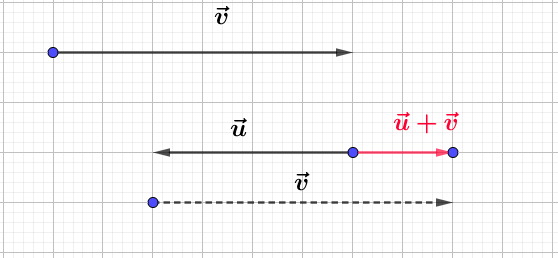
h)
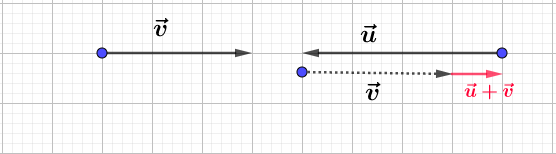
Exercice 2
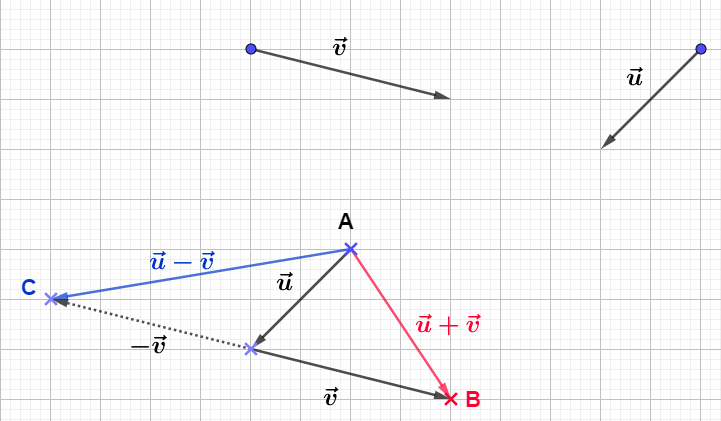
Exercice 3
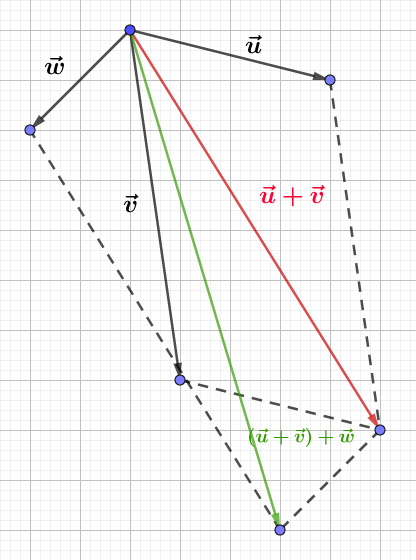
a) On construit successivement deux parallélogrammes, le premier sur $\vec{u}$ et $\vec{v}$, dont la diagonale donne le vecteur $\vec{u}+\vec{v}$, puis le second sur $\vec{u}+\vec{v}$ et $\vec{w}$, dont la diagonale donne le vecteur $\vec{u}+\vec{v}+\vec{w}.$
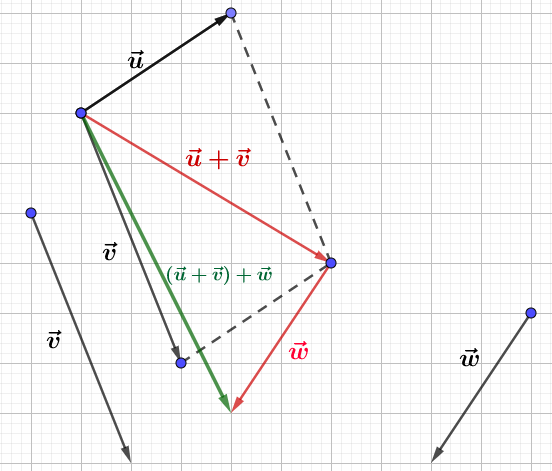
b) On construit $\vec{u}+\vec{v}$ puis, "au bout" de ce vecteur, on construit un représentant du vecteur $\vec{w}.$
c)
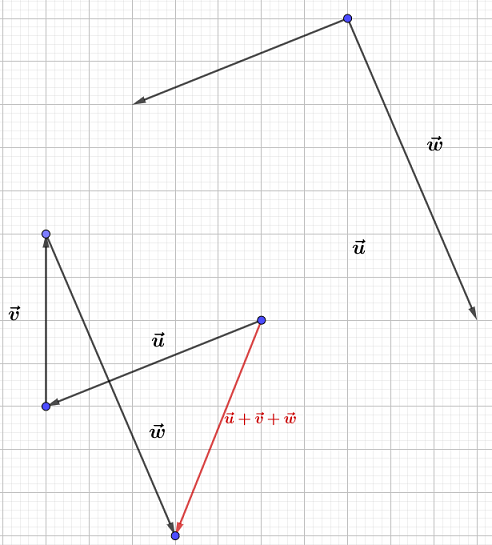
d)
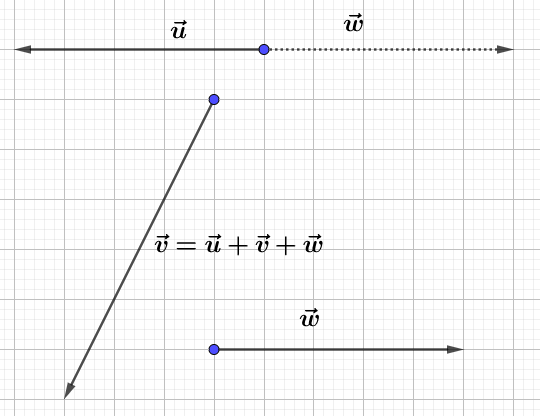
Ici, on remarque que $\vec{u}+\vec{w}=\vec{0}$, de sorte que $\vec{u}+\vec{v}+\vec{w}=\vec{v}\ !$
Exercice 4
$\centerdot\ E$ est un point de $(AB)$ et $\overrightarrow{AE}$ a le même sens que $\overrightarrow{AB}$, donc $E\in[AB).$ On partage $[AB]$ en trois parties de même longueur (voir le programme de Troisième) et on compte cette longueur quatre fois à partir de $A.$
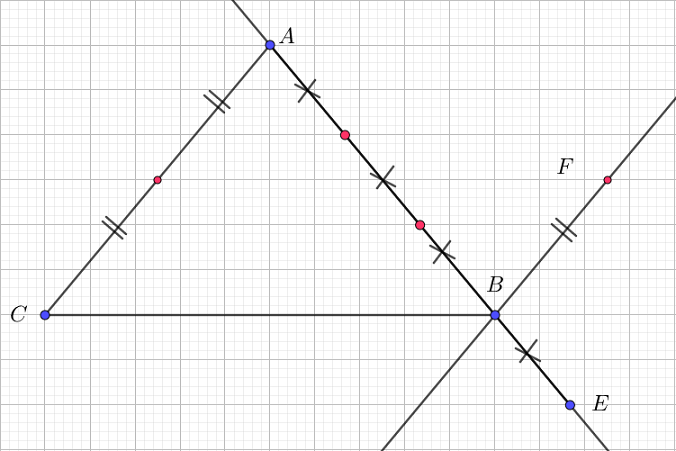
$\centerdot\ F$ est sur la parallèle à $(AC)$ passant par $B$ et $\overrightarrow{BF}$ a le sens contraire de $\overrightarrow{AC}.$ On partage $[AC]$ en deux parties et on prend une fois cette longueur à partir de $B.$
Exercice 5
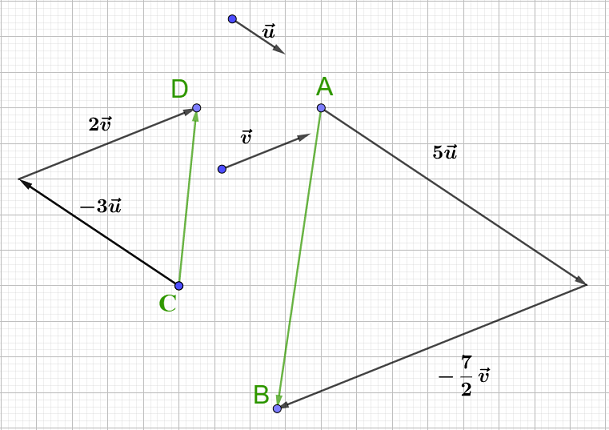
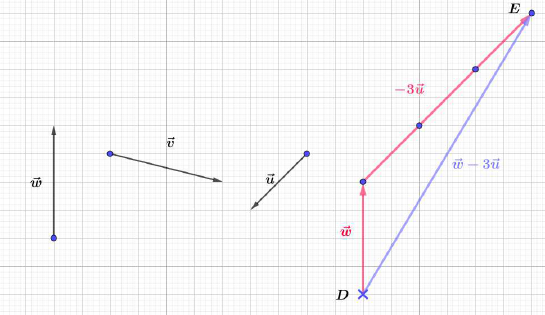
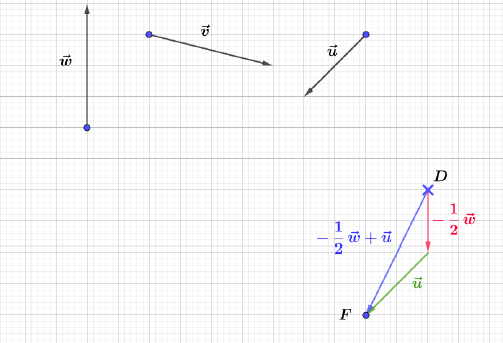
A partir d'un point arbitraire $A$, tracer une parallèle à la direction de $\vec{u}$, puis construire le vecteur $5\vec{u}$ par la méthode de l'exercice précédent (reporter 5 fois la longueur de $\vec{u}$ dans le même sens).
Puis, à l'extrémité du vecteur ainsi obtenu, tracer la demi-droite parallèle et de sens contraire à $\vec{v}$, puis reporter sur cette demi-droite 3.5 fois la longueur de $\vec{v}.$ On obtient le vecteur $\dfrac{7}{2}\vec{v}.$
En joignant l'origine du premier vecteur à l'extrémité du second, on obtient le vecteur $5\vec{u}-\dfrac{7}{2}\vec{v}.$
La méthode est la même pour le vecteur $-3\vec{u}+2\vec{v}.$
Exercice 6
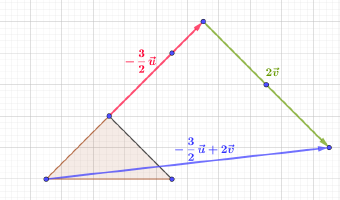
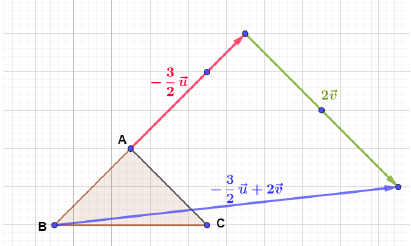
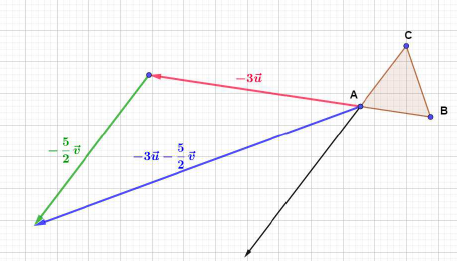
Exercice 7
Exercice 8
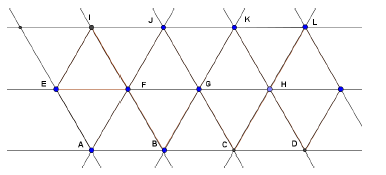
a) $\overrightarrow{IL}=\overrightarrow{IK}+\overrightarrow{KL}\quad$ b) $\overrightarrow{CD}=\overrightarrow{CE}+\overrightarrow{ED}$
c) $\overrightarrow{CD}=\overrightarrow{CJ}+\overrightarrow{JD}\quad$ d) $\overrightarrow{CD}=\overrightarrow{CH}+\overrightarrow{HD}$
e) $\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}\quad$ f) $\overrightarrow{HD}=\overrightarrow{HB}+\overrightarrow{BD}$
g) $\overrightarrow{PQ}=\overrightarrow{PA}+\overrightarrow{AQ}\quad$ h) $\overrightarrow{AQ}=\overrightarrow{AB}+\overrightarrow{BQ}$
i) $\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DJ}+\overrightarrow{JH}=\overrightarrow{AH}\quad$ j) $\overrightarrow{AB}=\overrightarrow{AK}+\overrightarrow{KP}+\overrightarrow{PB}$
k) $\overrightarrow{BA}=\overrightarrow{BD}+\overrightarrow{DC}+\overrightarrow{CA}$
Exercice 9
1) $\overrightarrow{AE}+\overrightarrow{AF}=\overrightarrow{AI}\quad$ 2) $\overrightarrow{AE}+\overrightarrow{EK}=\overrightarrow{AK}$
3) $\overrightarrow{EG}+\overrightarrow{GE}=\vec{0}\quad$ 4) $\overrightarrow{EG}+\overrightarrow{AF}=\overrightarrow{EK}$
Exercice 10
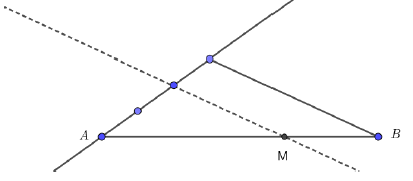
a) On introduit $A$ dans le vecteur $\overrightarrow{MA}$ par la relation de Chasles, puis on développe en utilisant les propriétés du calcul vectoriel.
$\begin{array}{rcl} \overrightarrow{MA}+3\overrightarrow{MB}=\vec{0}&\Leftrightarrow&\overrightarrow{MA}+3(\overrightarrow{MA}+\overrightarrow{AB})=\vec{0}\\ \\ &\Leftrightarrow&\overrightarrow{MA}+3\overrightarrow{MA}+3\overrightarrow{AB}=\vec{0}\\ \\ &\Leftrightarrow&4\overrightarrow{MA}+3\overrightarrow{AB}=\vec{0}\end{array}$
b) La relation $4\overrightarrow{MA}+3\overrightarrow{AB}=\vec{0}$ s'écrit aussi $3\overrightarrow{AB}=-4\overrightarrow{MA}=4\overrightarrow{AM}$ ou encore $\overrightarrow{AM}=\dfrac{3}{4}\overrightarrow{AB}$
Construction du point $M$
Exercice 11
a) $\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{BJ}\quad$ b) $\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}$
c) $\overrightarrow{MN}=\overrightarrow{MP}+\overrightarrow{PN}\quad$ d) $\overrightarrow{FE}=\overrightarrow{FP}+\overrightarrow{PG}+\overrightarrow{GE}$
e) $\overrightarrow{HJ}=\overrightarrow{HI}+\overrightarrow{IJ}\quad$ f) $\overrightarrow{JM}=\overrightarrow{JK}+\overrightarrow{KM}$
g) $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}=\overrightarrow{AD}\quad$ h) $\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}$
Exercice 12
1) En suivant la suggestion de l'énoncé, on a : $\vec{v}_{_{M}}=2\overrightarrow{MA}-5(\overrightarrow{MA}+\overrightarrow{AB})+3(\overrightarrow{MA}+\overrightarrow{AC}).$ Après simplification, les termes "en $\overrightarrow{MA}$"disparaissent et on obtient : $\vec{v}_{_{M}}=-5\overrightarrow{AB}+3\overrightarrow{AC}\ :$ c'est bien un vecteur constant car la lettre $M$ ne figure plus dans cette écriture
2) Méthode analogue au 1) ; on trouve que ce vecteur est égal à $\overrightarrow{AB}+2\overrightarrow{AC}$
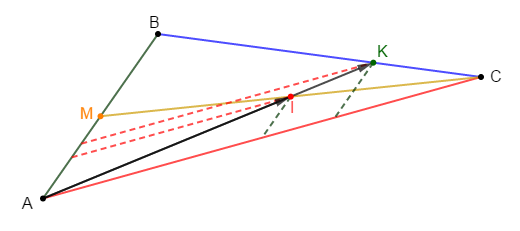
Exercice 34
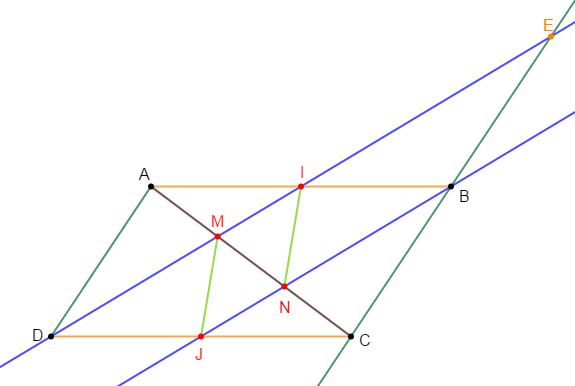
$ABCD$ est un parallélogramme, $I$ milieu de $[AB]\ $ et $\ J$ celui de $[CD]$
1) Démontrons que les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
Pour cela, il suffit juste de montrer que les vecteurs $\overrightarrow{ID}\ $ et $\ \overrightarrow{BJ}$ sont colinéaires.
En utilisant la relation de Chasles, on a :
$$\overrightarrow{ID}=\overrightarrow{IB}+\overrightarrow{BJ}+\overrightarrow{JD}\quad(*)$$
Comme $I$ milieu de $[AB]\ $ et $\ J$ milieu de $[CD]$ alors :
$\overrightarrow{IB}=\dfrac{1}{2}\overrightarrow{AB}\ $ et $\ \overrightarrow{JD}=-\dfrac{1}{2}\overrightarrow{DC}$
Or, $\overrightarrow{AB}=\overrightarrow{DC}$ car $ABCD$ est un parallélogramme donc, $\overrightarrow{IB}=-\overrightarrow{JD}$
Par suite, en reportant dans l'égalité $(*)$, on obtient :
$\begin{array}{rcl}\overrightarrow{ID}&=&\overrightarrow{IB}+\overrightarrow{BJ}+\overrightarrow{JD}\\\\&=&-\overrightarrow{JD}+\overrightarrow{BJ}+\overrightarrow{JD}\\\\&=&\overrightarrow{BJ}\end{array}$
Ainsi, $\overrightarrow{ID}=\overrightarrow{BJ}$
Ce qui signifie que $\overrightarrow{ID}\ $ et $\ \overrightarrow{BJ}$ sont colinéaires.
Par conséquent, les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
Autre méthode :
On a : $\overrightarrow{IB}=\overrightarrow{DJ}$ alors, $IBJD$ est un parallélogramme.
Par suite, $\overrightarrow{ID}=\overrightarrow{BJ}$
D'où, les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
2) a) Construisons les points $M\ $ et $\ N$ tels que $\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}\ $ et $\ \overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}$
b) Démontrons que les points $M\ $ et $\ N$ appartiennent respectivement aux droites $(ID)\ $ et $\ (JB)$
Pour cela, il suffit de prouver que $D\;,\ M\;,\ I$ sont alignés de même que $B\;,\ N\;,\ J$
Ce qui revient donc à montrer que $\overrightarrow{IM}=k\overrightarrow{ID}\ $ et $\ \overrightarrow{JN}=k'\overrightarrow{JB}$ avec $k\ $ et $\ k'$ deux nombres réels.
On a :
$\begin{array}{rcl}\overrightarrow{IM}&=&\overrightarrow{IA}+\overrightarrow{AM}\quad\text{or, }\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}\\\\&=&\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{AC}\\\\&=&\overrightarrow{IA}+\dfrac{1}{3}\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\\\\&=&\dfrac{1}{3}\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{DC}\\\\&=&\dfrac{1}{3}\left(\overrightarrow{IA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\left(2\overrightarrow{IA}+\overrightarrow{DC}\right)\quad\text{or, }2\overrightarrow{IA}=\overrightarrow{BA}\\\\&=&\dfrac{1}{3}\overrightarrow{ID}+\dfrac{1}{3}\underbrace{\left(\overrightarrow{BA}+\overrightarrow{DC}\right)}_{=\vec{0}}\\\\&=&\dfrac{1}{3}\overrightarrow{ID}\end{array}$
Donc, $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}$
Ainsi, les points $D\;,\ M\;,\ I$ sont alignés et par conséquent, $M$ appartient à la droite $(ID).$
De la même manière, on a :
$\begin{array}{rcl}\overrightarrow{JN}&=&\overrightarrow{JC}+\overrightarrow{CN}\quad\text{or, }\overrightarrow{CN}=\dfrac{1}{3}\overrightarrow{CA}\\\\&=&\overrightarrow{JC}+\dfrac{1}{3}\overrightarrow{CA}\\\\&=&\overrightarrow{JC}+\dfrac{1}{3}\left(\overrightarrow{CB}+\overrightarrow{BA}\right)\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{2}{3}\overrightarrow{JC}+\dfrac{1}{3}\overrightarrow{BA}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{1}{3}\left(2\overrightarrow{JC}+\overrightarrow{BA}\right)\quad\text{or, }2\overrightarrow{JC}=\overrightarrow{DC}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{1}{3}\underbrace{\left(\overrightarrow{BA}+\overrightarrow{DC}\right)}_{=\vec{0}}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}\end{array}$
Donc, $\overrightarrow{JN}=\dfrac{1}{3}\overrightarrow{JB}$
Par suite, les points $J\;,\ N\;,\ B$ sont alignés.
D'où, $N$ appartient à la droite $(JB).$
3) Démontrons que $MINJ$ est un parallélogramme
Soit : $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}\ $ et $\ \overrightarrow{JN}=\dfrac{1}{3}\overrightarrow{JB}$
Or, d'après la question 1), on a : $\overrightarrow{ID}=\overrightarrow{BJ}$
Donc, $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}=\dfrac{1}{3}\overrightarrow{BJ}=-\overrightarrow{JN}$
Par suite, $\overrightarrow{IM}=\overrightarrow{NJ}$
D'où, $MINJ$ est un parallélogramme.
4) Soit $\{E\}=(ID)\cap(BC)$, montrons que $B$ est milieu de $[CE]$
En effet, dans le triangle $CDE$, la droite $(JB)$ parallèle à $(DE)$ et passant par $J$, milieu de $[CD]$, coupe $[CE]$ au point $B.$
Ainsi, d'après le théorème de la droite des milieux, $B$ est milieu de $[CE].$

Exercice 51
Dans un triangle $ABC$, on considère par $M$ le milieu de $[AB]$, par $I$ celui de $[MC]\ $ et $\ K$ le point tel que $\overrightarrow{CK}=\dfrac{1}{3}\overrightarrow{CB}$
1) Montrons que :
$$\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\quad\text{et}\quad\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}$$
On a :
$\begin{array}{rcl}\overrightarrow{AI}&=&\overrightarrow{AC}+\overrightarrow{CI}\quad\text{or, }I\ \text{ milieu de }[CM]\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CM}\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\left(\overrightarrow{CA}+\overrightarrow{AM}\right)\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AM}\quad\text{or, }M\ \text{ milieu de }[AB]\\\\&=&\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}\right)\\\\&=&\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{AB}\end{array}$
D'où, $\boxed{\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}}$
Soit :
$\begin{array}{rcl}\overrightarrow{AK}&=&\overrightarrow{AC}+\overrightarrow{CK}\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\left(\overrightarrow{CA}+\overrightarrow{AB}\right)\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{AB}\end{array}$
Alors, $\boxed{\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}}$
2) En déduisons que les points $A\;,\ I\;,\ K$ sont alignés.
Pour cela, il suffit de montrer que $\overrightarrow{AI}=\alpha\overrightarrow{AK}$ avec $\alpha$ un nombre réel non nul.
D'après la question précédente, on peut constater que $4\overrightarrow{AI}=3\overrightarrow{AK}$
Ainsi, $\overrightarrow{AI}=\dfrac{3}{4}\overrightarrow{AK}$
D'où, les points $A\;,\ I\;,\ K$ sont alignés.

Exercice 58
$ABCD$ est un trapèze tel que $\overrightarrow{BC}=2\overrightarrow{AD}$
Soit $k$ un réel et $M$ le point défini par $\overrightarrow{AM}=k\overrightarrow{AB}$
$M$ se projette en $K$ sur $(AC)$ parallèlement à $(BC)$ et en $N$ sur $(CD)$ parallèlement à $(BC)$
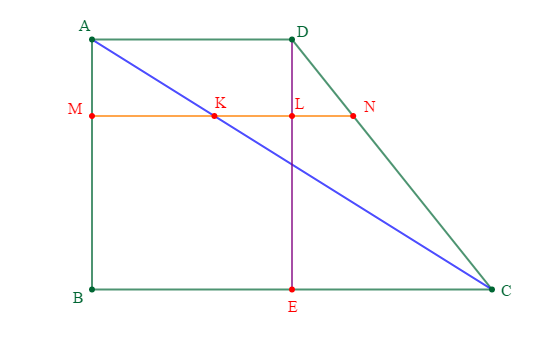
1) Montrons que $\overrightarrow{MK}=2k\overrightarrow{AD}\ $ et $\ \overrightarrow{NK}=(k-1)\overrightarrow{AD}$
On constate que $AMK\ $ et $\ ABC$ sont deux triangles en situation de Thalès donc, en appliquant le théorème de Thalès, on obtient :
$$\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{MK}}{\overline{BC}}\qquad(1)$$
Or, $\overrightarrow{AM}=k\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}=2\overrightarrow{AD}$
Donc, $\overline{AM}=k\overline{AB}\ $ et $\ \overline{BC}=2\overline{AD}$
Par suite, en remplaçant dans (1), on aura :
$\begin{array}{rcl}\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{MK}}{\overline{BC}}&\Leftrightarrow&\dfrac{k\overline{AB}}{\overline{AB}}=\dfrac{\overline{MK}}{2\overline{AD}}\\ \\&\Leftrightarrow&\dfrac{\overline{MK}}{2\overline{AD}}=k\\ \\&\Leftrightarrow&\overline{MK}=2k\overline{AD}\end{array}$
De plus $(MK)$ parallèle à $(BC)$ qui est parallèle à $(AD)$ donc, $(MK)$ est parallèle à $(AD)$
Ainsi, $\overline{MK}=2k\overline{AD}\ $ et $\ (MK)$ est parallèle à $(AD)$ telles que $[MK)\ $ et $\ [AD)$ orientées dans le même sens.
Par conséquent, $\overrightarrow{MK}=2k\overrightarrow{AD}\ $
Par ailleurs, on a : $\overrightarrow{MK}+\overrightarrow{KN}=\overrightarrow{MN}$
ce qui donne : $\overrightarrow{NK}=\overrightarrow{MK}-\overrightarrow{MN}$
Considérons $E$ le projeté de $D$ sur $(BC)$ parallèlement à $(AB)$ et $L$ le projeté de $M$ sur $(DE)$ parallèlement à $(BC)$
On a : $\overrightarrow{MN}=\overrightarrow{ML}+\overrightarrow{LN}$
Or, $\overrightarrow{ML}=\overrightarrow{AD}$ donc, $\overline{ML}=\overline{AD}$
De plus, les triangles $DLN\ $ et $\ DEC$ étant en position de Thalès alors,
$$\dfrac{\overline{DL}}{\overline{DE}}=\dfrac{\overline{LN}}{\overline{EC}}\qquad(2)$$
Comme $\overline{DL}=\overline{AM}=k\overline{AB}\;;\ \overline{DE}=\overline{AB}\ $ et $\ \overline{EC}=\dfrac{1}{2}\overline{BC}=\overline{AD}$ alors, en remplaçant dans (2), on obtient :
$\begin{array}{rcl}\dfrac{\overline{DL}}{\overline{DE}}=\dfrac{\overline{LN}}{\overline{EC}}&\Leftrightarrow&\dfrac{k\overline{AB}}{\overline{AB}}=\dfrac{\overline{LN}}{\overline{AD}}\\ \\&\Leftrightarrow&\dfrac{\overline{LN}}{\overline{AD}}=k\\ \\&\Leftrightarrow&\overline{LN}=k\overline{AD}\end{array}$
Par ailleurs, comme $(LN)$ est parallèle à $(AD)$ avec $[LN)\ $ et $\ [AD)$ orientées dans le même sens alors, on peut conclure que $\overrightarrow{LN}=k\overrightarrow{AD}$
Ainsi, $\overrightarrow{MN}=\overrightarrow{ML}+\overrightarrow{LN}$
avec, $\overrightarrow{ML}=\overrightarrow{AD}\ $ et $\ \overrightarrow{LN}=k\overrightarrow{AD}$
Par suite, $\overrightarrow{MN}=\overrightarrow{AD}+k\overrightarrow{AD}$
Par conséquent, on aura :
$\begin{array}{rcl}\overrightarrow{NK}&=&\overrightarrow{MK}-\overrightarrow{MN}\\\\&=&2k\overrightarrow{AD}-(\overrightarrow{AD}+k\overrightarrow{AD})\\\\&=&(2k-k-1)\overrightarrow{AD}\\\\&=&(k-1)\overrightarrow{AD}\end{array}$
D'où, $\overrightarrow{NK}=(k-1)\overrightarrow{AD}$
2) Déterminons le réel $k$ pour que $K$ soit le milieu de $[MN]$
$K$ milieu de $[MN]$ si, et seulement si, $\overrightarrow{MK}+\overrightarrow{NK}=\vec{0}$
On a :
$\begin{array}{rcl}\overrightarrow{MK}+\overrightarrow{NK}=\vec{0}&\Leftrightarrow&2k\overrightarrow{AD}+(k-1)\overrightarrow{AD}=\vec{0}\\ \\&\Leftrightarrow&(2k+k-1)\overrightarrow{AD}=\vec{0}\quad\text{or, }\ \overrightarrow{AD}\neq\vec{0}\\ \\&\Leftrightarrow&3k-1=0\\ \\&\Leftrightarrow&k=\dfrac{1}{3}\end{array}$
Ainsi, $K$ milieu de $[MN]$ si, et seulement si, $k=\dfrac{1}{3}$
Déterminons le réel $k$ pour que $\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}$
On sait que : $\overrightarrow{MN}=\overrightarrow{MK}-\overrightarrow{NK}$
Donc,
$\begin{array}{rcl}\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}&\Leftrightarrow&\overrightarrow{MK}-\overrightarrow{NK}=\dfrac{3}{2}\overrightarrow{AD}\\ \\&\Leftrightarrow&2k\overrightarrow{AD}-(k-1)\overrightarrow{AD}=\dfrac{3}{2}\overrightarrow{AD}\\ \\&\Leftrightarrow&2k\overrightarrow{AD}-(k-1)\overrightarrow{AD}-\dfrac{3}{2}\overrightarrow{AD}=\vec{0}\\ \\&\Leftrightarrow&\left(2k-k+1-\dfrac{3}{2}\right)\overrightarrow{AD}=\vec{0}\quad\text{or, }\ \overrightarrow{AD}\neq\vec{0}\\ \\&\Leftrightarrow&k-\dfrac{1}{2}=0\\ \\&\Leftrightarrow&k=\dfrac{1}{2}\end{array}$
D'où, $\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}$ si, et seulement si, $k=\dfrac{1}{2}$
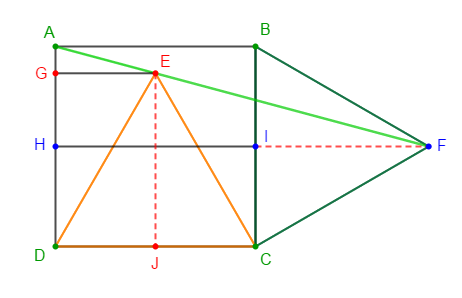
Exercice 59
Soit $ABCD$ un carré. On construit sur $[DC]$ et à l'intérieur du carré le triangle équilatéral $DCE.$
On construit sur $[BC]$ et à l'extérieur du carré le triangle équilatéral $BCF.$

1) Exprimons les vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}.$
Soit :
$\begin{array}{rcl}\overrightarrow{AE}&=&\overrightarrow{AG}+\overrightarrow{GE}\\ \\&=&\overrightarrow{AD}-\overrightarrow{GD}+\overrightarrow{GE}\end{array}$
Or, $\overrightarrow{GD}=\overrightarrow{EJ}$ et le triangle $DCE$ est équilatéral donc, $\overrightarrow{EJ}=\dfrac{\sqrt{3}}{2}\overrightarrow{AD}$
De plus, $\overrightarrow{GE}=\dfrac{1}{2}\overrightarrow{AB}$
Donc,
$\begin{array}{rcl}\overrightarrow{AE}&=&\overrightarrow{AD}-\overrightarrow{GD}+\overrightarrow{GE}\\ \\&=&\overrightarrow{AD}-\dfrac{\sqrt{3}}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\\ \\&=&\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2-\sqrt{3}}{2}\overrightarrow{AD}\end{array}$
D'où, $\boxed{\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2-\sqrt{3}}{2}\overrightarrow{AD}}$
Soit :
$\begin{array}{rcl}\overrightarrow{AF}&=&\overrightarrow{AH}+\overrightarrow{HF}\\ \\&=&\overrightarrow{AH}+\overrightarrow{HI}+\overrightarrow{IF}\end{array}$
Comme le triangle $BCF$ est équilatéral alors, $\overrightarrow{IF}=\dfrac{\sqrt{3}}{2}\overrightarrow{AB}$
De plus, $\overrightarrow{HI}=\overrightarrow{AB}\ $ et $\ \overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}$
Donc,
$\begin{array}{rcl}\overrightarrow{AF}&=&\overrightarrow{AH}+\overrightarrow{HI}+\overrightarrow{IF}\\ \\&=&\dfrac{1}{2}\overrightarrow{AD}+\overrightarrow{AB}+\dfrac{\sqrt{3}}{2}\overrightarrow{AB}\\ \\&=&\dfrac{1}{2}\overrightarrow{AD}+\dfrac{2+\sqrt{3}}{2}\overrightarrow{AB}\end{array}$
Ainsi, $\boxed{\overrightarrow{AF}=\dfrac{2+\sqrt{3}}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}}$
2)En déduisons que les points $A\;,\ E\;,\ F$ sont alignés.
On a :
$\begin{array}{rcl}\overrightarrow{AF}&=&\dfrac{2+\sqrt{3}}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\\ \\&=&(2+\sqrt{3})\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2-\sqrt{3}}{2}\overrightarrow{AD}\right)\\ \\&=&(2+\sqrt{3})\overrightarrow{AE}\end{array}$
Ainsi, $\overrightarrow{AF}=k\overrightarrow{AE}$ avec $k$ réel.
Par conséquent, les points $A\;,\ E\;,\ F$ sont alignés.
Auteur:
Mouhamadou Ka & Diny Faye

Commentaires
Anonyme (non vérifié)
mar, 01/29/2019 - 14:32
Permalien
pertinant
Anonyme (non vérifié)
dim, 10/04/2020 - 20:40
Permalien
Merci
Anonyme 23 (non vérifié)
mer, 12/16/2020 - 22:25
Permalien
Demande d aide
Anonyme (non vérifié)
sam, 01/09/2021 - 16:35
Permalien
Bien fait
Anonyme (non vérifié)
mar, 01/12/2021 - 22:11
Permalien
Intéressant.
Anonyme (non vérifié)
sam, 01/16/2021 - 14:05
Permalien
j'aimerais bien voir la
Anonyme (non vérifié)
mer, 01/20/2021 - 22:03
Permalien
Intéressant
Modou Diouf (non vérifié)
ven, 01/22/2021 - 00:04
Permalien
J ai besoin de la correction
HYACINTH A.B.MENDY (non vérifié)
mer, 01/27/2021 - 09:04
Permalien
Plus d'exercices merci.
Thiam (non vérifié)
mer, 01/27/2021 - 17:42
Permalien
Bonjour. J aurais besoin de
sqmqne (non vérifié)
mer, 02/03/2021 - 22:19
Permalien
la correction de l'exercice
Moussa ba (non vérifié)
jeu, 12/30/2021 - 16:27
Permalien
Correction des exercices
Anonyme (non vérifié)
sam, 11/19/2022 - 21:38
Permalien
J'ai besoin de la correction
Ndeye awa niang (non vérifié)
dim, 11/20/2022 - 12:30
Permalien
J'ai besoinde de la
maimouna diedhiou (non vérifié)
lun, 12/12/2022 - 23:27
Permalien
j'ai besoin la correction de
Mame Diarra (non vérifié)
lun, 12/26/2022 - 14:16
Permalien
J'aurais besoin la correction de l'exo 46
Salamoun (non vérifié)
sam, 02/04/2023 - 14:01
Permalien
J aurais besoin
Diallo (non vérifié)
mar, 12/12/2023 - 20:46
Permalien
Correction de exercices 36
Salamoun (non vérifié)
sam, 02/04/2023 - 14:01
Permalien
J aurais besoin
Salamoun (non vérifié)
sam, 02/04/2023 - 14:01
Permalien
J aurais besoin
Anonyme (non vérifié)
lun, 09/25/2023 - 22:16
Permalien
Cool
Anonyme (non vérifié)
lun, 09/25/2023 - 22:17
Permalien
Cool
Ndeye Fatou diop (non vérifié)
jeu, 12/14/2023 - 21:26
Permalien
J'ai besoin la correction de
Ndeye Fatou diop (non vérifié)
jeu, 12/14/2023 - 21:26
Permalien
J'ai besoin la correction de
Ndeye Fatou diop (non vérifié)
jeu, 12/14/2023 - 21:26
Permalien
J'ai besoin la correction de
Ajouter un commentaire