Vous êtes ici

Vecteurs - 3e

Classe:

Troisième

I. Rappels

I.1 Définitions et caractérisation

Un vecteur $AB$, noté $\overrightarrow{AB}$ et défini comme étant un segment orienté est principalement caractérisé par :

$-\ $ Sa direction : celle de la droite $(AB)$

$-\ $ Son sens : de $A$ vers $B\ ($celui de la demi-droite $[AB))$

$-\ $ Sa longueur : celle du segment $[AB]$

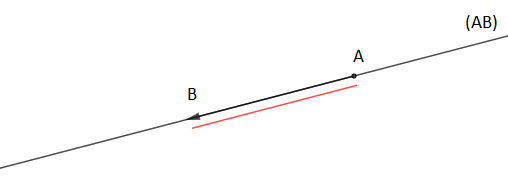
Les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BA}$ ont la même direction et la même longueur mais ils ont des sens contraires (opposés).

On notera $\overrightarrow{AB}=-\overrightarrow{BA}$

I.2 Translation

I.2.1 Construction et définition

$A$ et $A'$ étant donnés deux points, $B$ un point de ce plan ; on construit le point $B'$ tel que

$\centerdot\ \ (AA')\parallel(BB')$

$\centerdot\ \ \overrightarrow{AA'}\ $ et $\ \overrightarrow{BB'}$ sont de même sens

$\centerdot\ \ AA'=BB'$

et on l'appelle le translaté du point $B$ (ou image de $B$) par la translation qui transforme le point $A$ en $A'$ ou translation de vecteur $\overrightarrow{AA'}.$

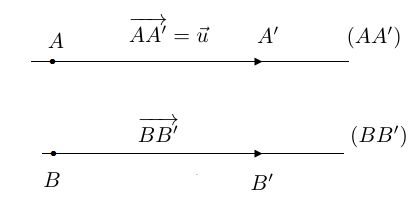
On notera $t_{\overrightarrow{AA'}}(B)=B'$ c'est à dire ; $\overrightarrow{AA'}=\overrightarrow{BB'}$

I.2.2 Propriétés

$\centerdot$

$$\text{Si }\left\lbrace\begin{array}{lll} \cdot\;(AA')\parallel(BB') \\ \\\cdot\;[AA')\text{ et }[BB')\;\text{ de même sens }\text{ alors, }\;\overrightarrow{AA'}=\overrightarrow{BB'}\\ \\\cdot\;AA'=BB'\end{array}\right.$$

Ainsi, $AA'BB'$ est un parallélogramme.

Par suite, si $\overrightarrow{AA'}=\overrightarrow{BB'}$ alors, $AA'BB'$ est un parallélogramme (nouvelle configuration du parallélogramme).

$\centerdot\ \ $ Si $I$ milieu de $[AB]$ alors, $\overrightarrow{AI}=\overrightarrow{IB}$ ou encore $\overrightarrow{IA}=-\overrightarrow{IB}$

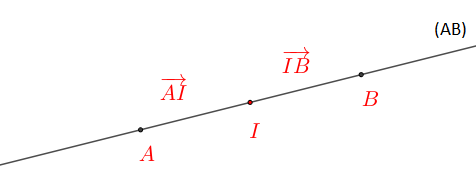
Ainsi, si $\overrightarrow{AI}=\overrightarrow{IB}$ ou $\overrightarrow{IA}=-\overrightarrow{IB}$ alors, $I$ milieu de $[AB].$

II. Addition vectorielle

II.1 Théorème et définition

Soit $\vec{u}\ $ et $\ \vec{v}$ deux vecteurs d'un plan et $A$ un point de ce plan.

On construit les points $B\ $ et $\ C$ ; translatés respectifs des points $A\ $ et $\ B$ par les translations respectives $t_{\vec{u}}\ $ et $\ t_{\vec{v}}.$

Le vecteur $\vec{w}=\overrightarrow{AC}$ associé aux translations successives $t_{\vec{u}}\ $ et $\ t_{\vec{v}}$ du point $A$ est appelé somme vectorielle des vecteurs $\vec{u}\ $ et $\ \vec{v}.$

On notera : $\vec{w}=\vec{u}+\vec{v}$ ou encore $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$

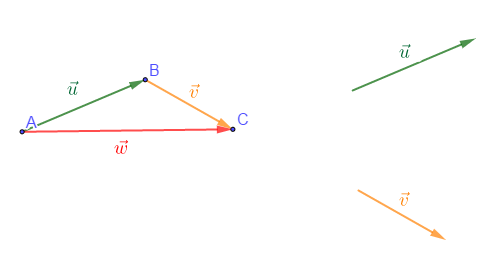
Le vecteur $\vec{w}$ est indépendant du point $A$ choisi mais dépend uniquement des vecteurs $\vec{u}\ $ et $\ \vec{v}.$

II.2 Relation de Chasles

La relation de Chasles est une interprétation de l'addition vectorielle.

Soit $A\;,\ B\ $ et $\ C$ trois points d'un plan, on a : $$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$$

Exemple :

Calculons les sommes vectorielles suivantes :

$\begin{array}{rcl}\overrightarrow{CS}+\overrightarrow{ST}+\overrightarrow{TP} & = & \overrightarrow{CT}+\overrightarrow{TP} \\ \\& = & \overrightarrow{CP} \end{array}$

$\begin{array}{rcl}\overrightarrow{RS}-\overrightarrow{TS} & = & \overrightarrow{RS}+\overrightarrow{ST} \\ \\& = & \overrightarrow{RT} \end{array}$

II.3 Commutativité et associativité

Soient $\vec{u}\;,\ \vec{v}\ $ et $\ \vec{w}$ trois vecteurs et un plan, on a :

$\centerdot\ \ \vec{u}+\vec{v}=\vec{v}+\vec{u}$

$\centerdot\ \ \vec{u}+(\vec{v}+\vec{w})=(\vec{u}+\vec{v})+\vec{w}$

Exemple : donnons la somme vectorielle suivante :

$\begin{array}{rcl}\overrightarrow{NA}+(\overrightarrow{AM}+\overrightarrow{CN}) & = & \left(\overrightarrow{NA}+\overrightarrow{AM}\right)+\overrightarrow{CN} \\ \\& = & \overrightarrow{NM}+\overrightarrow{CN} \\ \\& = & \overrightarrow{CN}+\overrightarrow{NM} \\ \\& = & \overrightarrow{CM} \end{array}$

II.4 vecteur nul

Par définition, le vecteur nul ; noté $\vec{0}$ est un vecteur qui a pour longueur 0.

Soit $\vec{u}$ un vecteur du plan, on a $\vec{u}+\vec{0}=\vec{0}+\vec{u}=\vec{u}.$

Et comme $\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{BB}$ alors, $\overrightarrow{BB}=\vec{0}$

Remarques :

Soient $A\ $ et $\ B$ deux points d'un plan, on a $\overrightarrow{AA}=\vec{0}\ $ et $\ \overrightarrow{AB}=\vec{0}$ si, et seulement si, $A=B.$

Le vecteur nul a toutes les directions possibles ; $t_{\vec{0}}(M)=M$

II.5 Vecteurs opposés

Quelque soit un vecteur $\vec{u}$ d'un plan, il existe un vecteur $\vec{u}'$ de ce plan tel que $\vec{u}+\vec{u}'=\vec{u}'+\vec{u}=\vec{0}$

Le vecteur $\vec{u}'$ est appelé le vecteur opposé de $\vec{u}$

On notera $$\vec{u}'=-\vec{u}$$

Soit donc $\overrightarrow{AB}$ un vecteur du plan ; on a : $\overrightarrow{AB}=-\overrightarrow{BA}.$

Ainsi,

$\begin{array}{rcl} \overrightarrow{AB}+\left(-\overrightarrow{AB}\right)&=&\overrightarrow{AB}+\overrightarrow{BA}\\ \\& = & \overrightarrow{AA} \\ \\& = & \vec{0} \end{array}$

Si $I$ milieu de $[AB]$ alors, $\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$

Si $\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$ alors, $I$ milieu de $[AB]$

Application :

Soit $I$ milieu d'un segment $[AB]$ d'un plan.

Démontrons que pour tout point $M$ de ce plan, on a : $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$

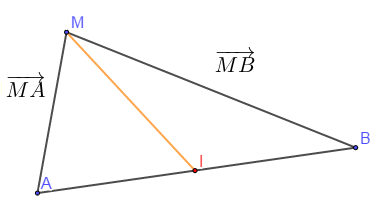
1er méthode

On a : $\overrightarrow{MA}=\overrightarrow{MI}+\overrightarrow{IA}$

$\overrightarrow{MB}=\overrightarrow{MI}+\overrightarrow{IB}$

Alors, $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{IB}$

Or, $I$ milieu d'un segment $[AB]$ donc, $\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}.$

Ainsi, $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$

2em méthode

On a : $I$ milieu d'un segment $[AB]$ alors, $\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$

Donc, $\overrightarrow{IM}+\overrightarrow{MA}+\overrightarrow{IM}+\overrightarrow{MB}=\vec{0}$

Ainsi, $\overrightarrow{MA}+\overrightarrow{MB}=-2\overrightarrow{IM}$

D'où, $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$

III. Multiplication d'un vecteur par un nombre réel

III.1 Exemple et définition

Soient $A\;,\ B\;,\ C\;,\ D\;,\ E\ $ et $\ F$ six points du plan tels que $\overrightarrow{AB}=\overrightarrow{BC}=\overrightarrow{CD}=\overrightarrow{DE}=\overrightarrow{EF}$

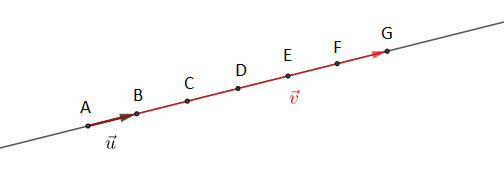
On a : $\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}$

Alors, $\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{AB}+\overrightarrow{AB}+\overrightarrow{AB}+\overrightarrow{AB}$

Donc, $\overrightarrow{AF}=5\overrightarrow{AB}$

En posant $\vec{u}=\overrightarrow{AB}\ $ et $\ \vec{v}=\overrightarrow{AF}$, on obtient : $\vec{v}=5\times\vec{u}.$

Ainsi, $\vec{v}$ est le produit du vecteur $\vec{u}$ par le réel $5.$

D'où, si deux vecteurs $\vec{u}\ $ et $\ \vec{v}$ ont la même direction, il existe un réel $k$ tel que $\vec{v}=k.\vec{u}.$

Le vecteur $\vec{v}$ est appelé le produit du vecteur $\vec{u}$ par le réel $k.$

Remarques :

$\centerdot\ \ $ Si $k>0$ alors, $\vec{v}=k.\vec{u}$ signifie que les vecteurs $\vec{v}\ $ et $\ \vec{u}$ ont la même direction, le même sens et que la longueur du vecteur $\vec{v}$ est égale à $k$ fois la longueur du vecteur $\vec{u}.$

$\centerdot\ \ $ Si $k<0$ alors, $\vec{v}=k.\vec{u}$ signifie que les vecteurs $\vec{v}\ $ et $\ \vec{u}$ ont la même direction, de sens opposés et que la longueur du vecteur $\vec{v}$ est égale à $k$ fois la longueur du vecteur $\vec{u}.$

$\centerdot\ \ $ Si $k=0$ alors, $\vec{v}=0.\vec{u}=\vec{0}$

III.2 Propriétés

Soient $\vec{u}\ $ et $\ \vec{v}$ deux vecteurs du plan, $a\ $ et $\ b$ deux nombres réels ; on a :

$\centerdot\ \ a.(\vec{u}+\vec{v})=a.\vec{u}+a.\vec{v}$

$\centerdot\ \ (a+b).\vec{u}=a.\vec{u}+b.\vec{u}$

$\centerdot\ \ a.(b.\vec{u})=(a.b).\vec{u}$

$\centerdot\ \ a.\vec{u}=\vec{0}$ si, et seulement si, $a=0$ ou $\vec{u}=\vec{0}$

III.3 Vecteurs colinéaires

Deux vecteurs $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires s'il existe un réel $k$ tel que $\vec{v}=k.\vec{u}.$

Deux vecteurs colinéaires ont la même direction.

Le vecteur nul est colinéaire à tout vecteur du plan.

III.4 Utilisation de la colinéarité

$\centerdot\ \ $ Les points $A\;,\ B\ $ et $\ C$ sont alignés si, et seulement si, $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ colinéaires.

$\centerdot\ \ $ Soient $I\ $ et $\ J$ deux points distincts, on a : $M\in\;(IJ)$ si, et seulement si, $\overrightarrow{IJ}\ $ et $\ \overrightarrow{IM}$ colinéaires.

$\centerdot\ \ $ Soient quatre points $A\;,\ B\;\ C\ $ et $\ D$ tels que $A\neq D$ et $B\neq C$, on a : $(AB)\parallel(DC)$ si, et seulement si, $\overrightarrow{AB}\ $ et $\ \overrightarrow{CD}$ colinéaires.

$\centerdot\ \ \overrightarrow{AC}=k.\overrightarrow{AB}$ alors $A\;,\ B\ $ et $\ C$ sont alignés. Et si :

$\cdot\ \ k<0$ alors, $A\in\;[BC]$

$\cdot\ \ k=0$ alors, $A=C$

$\cdot\ \ 0<k<1$ alors, $C\in\;[AB]$

$\cdot\ \ k=1$ alors, $B=C$

$\cdot\ \ k>1$ alors, $B\in\;[AC]$

III.5 Configuration de Thalès

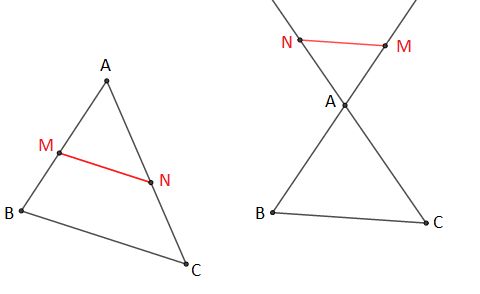
$\left\lbrace\begin{array}{lll} M\in\;[AB] \\ \\N\in\;[AC] \end{array}\right.\quad(MN)\parallel(BC)\ $ ou $\ \left\lbrace\begin{array}{lll} A\in\;[BM] \\ \\A\in\;[CN] \end{array}\right.$ avec $\left\lbrace\begin{array}{lll} \overrightarrow{AC}=k.\overrightarrow{AN} \\ \\\overrightarrow{BC}=k.\overrightarrow{MN}\end{array}\right.$

Auteur:

Abdoulaye Ba