FONCTION LOGARITHME NEPERIEN
Partie 1
 En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisé de Neper publie « Mirifici logarithmorum canonis descriptio ». En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisé de Neper publie « Mirifici logarithmorum canonis descriptio ».Dans cet ouvrage, qui est la finalité d’un travail de 20 ans, Neper présente un outil permettant de simplifier les calculs opératoires : le logarithme. Neper construit le mot à partir des mots grecs « logos » (logique) et arithmos (nombre). Toutefois cet outil ne trouvera son essor qu’après la mort de Neper. Les mathématiciens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ; 1660) reprennent et prolongent les travaux de Neper. Les mathématiciens de l’époque établissent alors des tables de logarithmes de plus en plus précises. L’intérêt d’établir ces tables logarithmiques est de permettre de substituer une multiplication par une addition (paragraphe II). Ceci peut paraître dérisoire aujourd’hui, mais il faut comprendre qu’à cette époque, les calculatrices n’existent évidemment pas, les nombres décimaux ne sont pas d’usage courant et les opérations posées telles que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le commerce demandent d’effectuer des opérations de plus en plus complexes. |
I. Définition
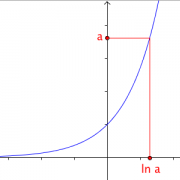 La fonction exponentielle est continue et strictement croissante sur $\mathbb{R}$, à valeurs dans $]0,+\infty[$ .
La fonction exponentielle est continue et strictement croissante sur $\mathbb{R}$, à valeurs dans $]0,+\infty[$ .
Pour tout réel a de $]0,+\infty[$ l'équation $e ^x = a$ admet une unique solution dans $\mathbb{R}$.
| Définition : On appelle logarithme népérien d'un réel strictement positif a, l'unique solution de l'équation $e^x=a$. On la note $\ln a$ La fonction logarithme népérien, notée $\ln$, est la fonction : \[\ln:]0;-\infty[ \rightarrow \mathbb{R}\\ x \rightarrow \ln x\] |
Exemple:
L'équation $e^{x}=5$ admet une unique solution. Il s'agit de $x=\ln 5$ .
A l'aide de la calculatrice, on peut obtenir une valeur approchée : $x≈ 1,61$.
Remarque:
Les courbes représentatives des fonctions exponentielle et logarithme népérien sont symétriques par rapport à la droite d'équation $y=x$ .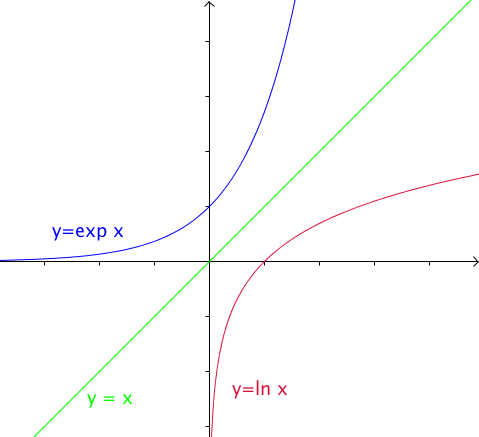
|
Conséquences : $\ln \frac{1}{e}=-1$ |
Démonstrations :
a) Par définition
b) - Car $e^{0}=1$
- Car $e^{1}=e$
- Car $e^{-1}=\frac{1}{e}$
c) Si on pose $y=e^{x}$ , alors $x=\ln y=\ln e^x$
d) Si on pose $y=\ln x$ , alors $x=e^y=e^{\ln x}$
Exemples: $e^{\ln 2}=2$ et $\ln e^4=4$
| Propriété: Pour tous réels x et y strictement positifs, on a : a) $\ln x=\ln y \iff=y$ b) $\ln x<\ln y \iff x<y$ |
Démonstration:
a) $x=y \iff e^{\ln x}=e^{\ln y} \iff \ln x=\ln y$
b) $x<y \iff e^{\ln x}=e^{\ln y} \iff \ln x=\ln y$
Méthode: Résoudre une équation ou une inéquation
Résoudre dans I les équations et inéquations suivantes :
a) $\ln x=2$ , $I=]0;+\infty[ $ b) $e^{x+1}=5$ ,$I= \mathbb{R}$ c) $ 3\ln x-4=8 $ , $ I=]0;+\infty[ $
d) $ln(6x-1)\geq2$ , $I=]\frac{1}{6};+\infty[ $ e)$e^{x}+54e^{x}>e^x$ , $ I=]0;+\infty[ $
a)$\ln x=2$
$\iff \ln x=\ln e^{2}$
$\iff x=e^{2}$ La solution est $e^2$ .
b) $e^{x+1}=5$
$\iff e^{x+1}=e^{\ln 5}$ La solution est $\ln 5-1$.
$\iff x+1=\ln 5$
$\iff x=\ln 5-1$
c) $3\ln x-4=8$
$\iff 3\ln x=12$
$\iff \ln x=4$
$\iff \ln x=\ln e^{4}$
$\iff x=e^4$ La solution est $e^{4}$.
d) $\ln (6x-1)\geq 2$
$\iff \ln (6x-1)\geq \ln e^{2}$
$\iff (6x-1)\geq e^{2}$ L'ensemble solution est donc $] \frac{e^{2}+1}{6};0[$ .
$\iff x\geq\frac{{e^{2}+1}}{6}$
e)$e^{x}+5 > 4e^{x}$
$\iff e^{x}>-4e^{x}$
$\iff -3e^{x}> -5$
$\iff e^{x}< \frac{5}{3}$
$\iff e^{x}< e^{\ln (\frac{5}{3})}$
$\iff x <\ln {\frac{5}{3}}$
L'ensemble solution est donc$ ]-\infty ;ln\frac{5}{3}[$
II. Propriété de la fonction logarithme népérien
1) Relation fonctionnelle
| Théorème : Pour réel x et y strictement positif, on a: $\ln(x\times y)=\ln x+ln y$. |
Remarque: Cette formule permet de transformer un produit en somme.
Démonstration:
$e^{\ln (x\times y)}=x\times y=e^{\ln x}\times e^{\ln y}=e^{\ln x+\ln y}$
Donc $\ln (x\times y) = \ln x+\ln y$
 Remarque : Cette formule permet de transformer un produit en somme.
Remarque : Cette formule permet de transformer un produit en somme.
Ainsi, celui qui aurait à effectuer 36 x 62, appliquerait cette formule, soit :
log(36 x 62) = log(36) + log(62) ≈ 1,5563 + 1,7924 (voir table ci-contre)
L’addition étant beaucoup plus simple à effectuer que la multiplication, on trouve facilement :
log(36 x 62) ≈ 3,3487
En cherchant dans la table, le logarithme égal à 3,3487, on trouve 2232, soit : 36 x 62 = 2232.
| Corollaires: Pour tous réels x et y strictement positifs, on a : a) $\ln \frac{1}{x}=-\ln x$ b) $\ln \frac{x}{y}=\ln x-\ln y$ c) $\ln \sqrt{x}=\frac{1}{2}\ln x$ d) $\ln x^n=n\ln x$ avec n entier relatif |
Démonstrations:
a) $\ln \frac{1}{x}+\ln x =\ln (\frac{1}{x}\times{x})=\ln 1=0 $
b) $\ln \frac{x}{y}=\ln (x\times \frac{1}{y})=\ln x+\ln \frac{1}{y}=\ln x-\ln y$
c) $2\ln \sqrt{x}=\ln \sqrt{x}+\ln \sqrt{x}=\ln (\sqrt{x}\times \sqrt{x})=\ln x$
d) $e^{n\ln x}=(e^{\ln x})^n=x^n=e^{\ln (x^n)}$
Donc $n\ln x=\ln (x^{n})$
Exemples :
a) $\ln \frac{1}{2}=-\ln 2$ b) $\ln \frac{3}{4}=\ln 3-\ln 4$ c) $\ln \sqrt{5}=\frac{1}{2}\ln 5$ d) $\ln 64=\ln 8^{2}=2\ln 8$
Méthode : Simplifier une expression
$A=\ln (3-\sqrt{5})+\ln (3+\sqrt{5})$ $B=3\ln 2+\ln 5-2\ln 3$ $C= \ln e^{2}-\ln \frac{1}{e}$
$A=\ln (3-\sqrt{5})+\ln (3+\sqrt{5})$
=$\ln (3-\sqrt{5})+\ln (3+\sqrt{5})$
=$\ln (9-5)$
=$\ln 4$
$B=3\ln 2+\ln 5-2\ln 3$
=$\ln 2^{3}+\ln 5-\ln 3^{2}$
=$\ln 2^{3}+\ln 5-\ln 3^{2}$
=$\ln \frac{2^{3}X5}{3^{2}}$
=$\ln \frac{40}{9}$
$C= \ln e^{2}-\ln \frac{1}{e}$$2\ln e-\ln 2+\ln e$
=$2\ln e-\ln 2+\ln e$
=$2-\ln 2+1$
=$3-\ln 2$
Méthode : Résoudre une équation ou une inéquation
1) Résoudre dans l’équation : $6^x=2$
2) Résoudre dans $]0;+\infty[$ l'équation : $x^{5}=3$
3) 8 augmentations successives de t % correspondent à une augmentation globale de 30 %. Donner une valeur approchée de t.
1) $6^{x}=2$
$\iff \ln (6^{x})=\ln 2$
$\iff x\ln 6=\ln 2$ La solution est $\frac{\ln 6}{\ln 2}$.
$\iff x=\frac{\ln 6}{\ln 2}$
2) Comme $x>0$ , on a :
$x^{5}=3$
$\iff \ln (x^{5})=\ln 3$
$\iff 5\ln x=\ln 3$
$\iff \ln x=\frac{1}{5}\ln 3$
$\iff \ln x=\ln (3^{\frac{1}{5}})$
$\iff x=3^{\frac{1}{5}}$
La solution est $x=3^{\frac{1}{5}}$ .
Remarque :$3^{\frac{1}{5}}$ se lit "racine cinquième de 3" et peut se noter $^5\sqrt{3}$ .
3) Le problème revient à résoudre dans $]0;+\infty[$ l'équation :$(1+\frac{t}{100})^{8}=1,3 $
$\iff \ln (1+\frac{t}{100})^{8}=\ln 1,3$
$\iff 8\ln (1+\frac{t}{100})=\ln 1,3$
$\iff \ln (1+\frac{t}{100})=\frac{1}{8}\ln 1,3$
$\iff \ln (1+\frac{t}{100})=\ln (1,3^\frac{1}{8})$
$\iff \ln (1+\frac{t}{100})=\ln (1,3^\frac{1}{8})$
$\iff 1+\frac{t}{100}=1,3^\frac{1}{8}$
$\iff t=100(1,3^\frac{1}{6}-1)≈3,3$
Une augmentation globale de 30 % correspond à 8 augmentations successives d'environ 3,3 %.
Partie 2
I. Etude de la fonction logarithme népérien
1) Continuité et dérivabilité
| Propriété: La fonction logarithme népérien est continue sur $]0;+\infty[$ . |
- Admis -
| Propriété : La fonction logarithme népérien est dérivable sur $]0;+\infty[$ et $(\ln x)'=\frac{1}{x}$ . |
Démonstration :
Nous admettons que la fonction logarithme népérien est dérivable sur $]0;+\infty[$ .
Posons $f(x)=e^{\ln x}$ .
Alors $f'(x)=(\ln x)'e^{\ln x} =x(\ln x)'$
Comme $f(x)=x$ , on a $f'(x)=1$ .
Donc $x(\ln x)'=1$ et donc $(\ln x)'=\frac{1}{x}$ .
Exemple :
Dériver la fonction suivante sur l'intervalle $]0;+\infty[$ :$f(x)=\frac{\ln x}{x}$
$f'(x)=\frac{\frac{1}{x}\times x-\ln x\times 1}{x^2}=\frac{1-\ln x}{x^2}$
2) Variations
| Propriété: La fonction logarithme népérien est strictement croissante sur $]0,+\infty[$. |
Démonstration:
Pour tout réel x > 0,$(lnx)'=\frac{1}{x}$ .
3) Convexité
| Propriété : La fonction logarithme népérien est concave sur sur $]0,+\infty[$ . |
Démonstration :
Pour tout réel x > 0, $(\ln x)'=\frac{1}{x}$ .
$(\ln x)''=\frac{1}{x^{2}}$
donc la dérivée de la fonction \ln est strictement décroissante sur$]0;+\infty[$
et donc la fonction logarithme népérien est concave sur cet intervalle.
4) Limites aux bornes
| Propriété: $\lim\limits_{x\to +\infty} \ln x = +\infty$ et $\lim\limits_{\underset{x>0}{x \to 0}} \ln x=-\infty$ |
On peut justifier ces résultats par symétrie de la courbe représentative de la fonction exponentielle.
5) Tangentes particulières
Rappel : Une équation de la tangente à la courbe $Cf$ au point d'abscisse a est :
$y=f'(a)(x-a)+f(a).$
Dans le cas de la fonction logarithme népérien, l'équation est de la forme :
$y=\frac{1}{a}(x-a)+\ln a$.
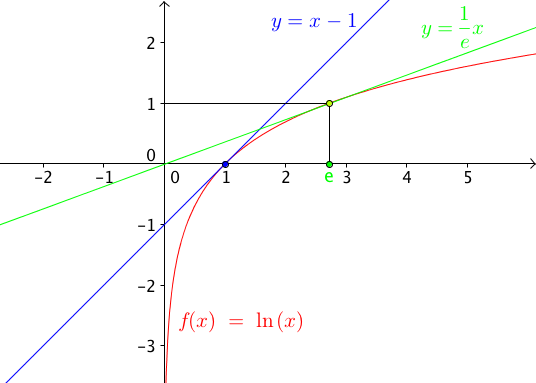
- Au point d'abscisse 1, l'équation de la tangente est $y=\frac{1}{1}(x-1)+\ln 1$ soit : $y=x-1$ .
- Au point d'abscisse e, l'équation de la tangente est $y=\frac{1}{e}(x-e)+\ln e$ soit :$y=\frac{1}{e}x$ .
6) Courbe représentative
On dresse le tableau de variations de la fonction logarithme népérien +
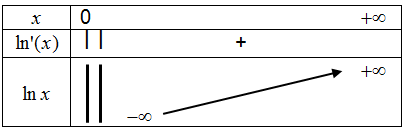
Valeurs particulières : $ln 1=0$ $ln e=1$
Méthode : Etudier les variations d'une fonction
1) Déterminer les variations de la fonction f définie sur$]0;+\infty[$ par $f(x)=3-x+\ln x$ .
2) Etudier la convexité de la fonction $f$.
1) Sur$]0;+\infty[$ , on a $ f'(x)=-1+\frac{2}{x}=\frac{2-x}{x}$ .
Comme $x>0$,$f'(x)$ est du signe de $2-x$ .
La fonction f est donc strictement croissante sur $]0;2]$ et strictement décroissante
sur $[2;+\infty[$ .
On dresse le tableau de variations :
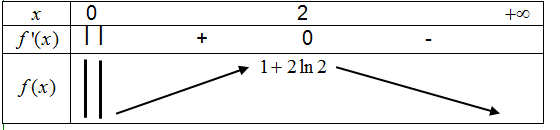
$f(2)=3+2+2ln 2=1+2\ln 2$
2) Sur $]0;+\infty[$ , on a $f''(x)=\frac{-1\times x-(2-x)\times 1}{x^2}=\frac{-x-2+x}{x^2}=-\frac{2}{x^2}<0$.
La fonction $f'$ est donc décroissante sur $]0;+\infty[$ . On en déduit que la fonction $f$ est concave sur $]0;+\infty[$ .
II. Positions relatives
| Propriété : La courbe représentative de la fonction exponentielle est au-dessus de la droite d'équation y=x . La droite d'équation y=x est au-dessus de la courbe représentative de la fonction logarithme népérien. |
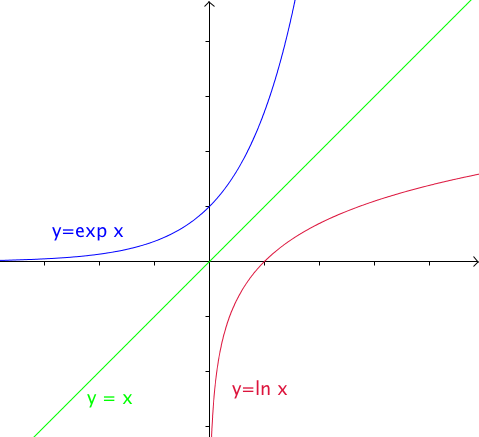
Démonstration :
- On considère la fonction $f$ définie sur par $f(x)=e^{x}-x$ .
$f''(x)=e^{x}-1$
$f(x)=0$
$\iff e^{x}-1$
$\iff e^{x}=1$
$\iff x=0$
On a également $f(0)=e^{0}-0=1 >0$.
On dresse ainsi le tableau de variations :
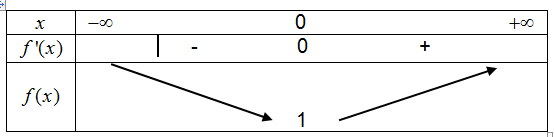
On en déduit que pour tout x de $\mathbb{R}$, on a $f(x)=e^{x}-x>0$ soit $e^{x} >x$
- On considère la fonction g définie sur par $]0;+\infty[$ par $g(x)=x-\ln x$.
$g(x)=1-\frac{1}{x}=\frac{x-1}{x}$.
Comme $x>0$ , $f'(x)$ est du signe de $x-1$ .
On a également $g(1)=1-ln1=1>0$.
On dresse ainsi le tableau de variations :
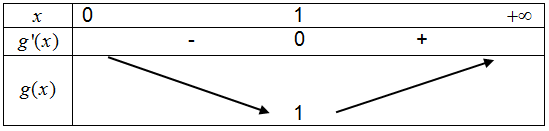
On en déduit que pour tout x de $]0;+\infty[$ , on a $g(x)=x-\ln x >0$ soit $x >\ln x$.

Ajouter un commentaire