Série d'exercices sur les barycentres 1er S
Rappels sur les vecteurs
Exercice 1
$ABCD$ est un quadrilatère quelconque, $I$ le milieu de $[AD]\ $ et $\ J$ celui de $[BC].$
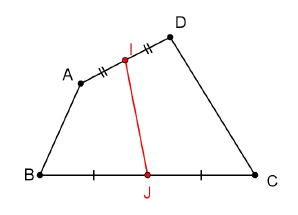
1) Ecrire $\overrightarrow{IJ}$ comme la somme de $\overrightarrow{AB}$ et de deux autres vecteurs que l'on précisera.
2) Décomposer le même $\overrightarrow{IJ}$ en utilisant $\overrightarrow{DC}.$
3) En déduire que $2\overrightarrow{IJ}=\overrightarrow{AB}+\overrightarrow{DC}.$
Exercice 2
$ABCD$ est un parallélogramme de centre $O$, $\ I$ est le milieu de $[AB]\ $ et $\ J$ le point tel que $\overrightarrow{DJ}=\overrightarrow{OC}.$
1) Exprimer $\overrightarrow{OI}$ en fonction de $\overrightarrow{BC}$.
2) Justifier les égalités : $\overrightarrow{BC}=\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{OJ}.$
3) Quel théorème vous permet de conclure que $O\;,\ I\ $ et $\ J$ sont alignés ?
Exercice 3
$ABC$ est un triangle, $E$ est tel que $\overrightarrow{AE}=\dfrac{1}{3}\overrightarrow{BC}$, $\ I$ est tel que $\overrightarrow{CI}=\dfrac{2}{3}\overrightarrow{CB}\ $ et $\ F$ est tel que $\overrightarrow{AF}=\dfrac{1}{3}\overrightarrow{AC}.$
Démontrer que $I$, $E$ et $F$ sont alignés.
Exercice 4
$ABCD$ est un parallélogramme, $M\;,\ N\;,\ Q$ sont tels que :
$$\overrightarrow{DM}=\dfrac{4}{5}\overrightarrow{DA}\;,\ \overrightarrow{AN}=\dfrac{3}{4}\overrightarrow{AB}\;,\ \overrightarrow{CQ}=\dfrac{2}{3}\overrightarrow{CD}$$
La parallèle à $(MQ)$ menée par $N$ coupe $(BC)$ en $P$. Il s'agit de trouver le coefficient $k$ de colinéarité tel que $\vec{BP}=k\overrightarrow{AD}$.
Considérons le repère $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD}).$
1) Calculer les coordonnées des points $M$, $\ N\ $ et $\ Q.$
2) Justifier que $P$ a pour coordonnées $(1\;;\ k).$
3) En déduire que les vecteurs $\overrightarrow{MQ}\ $ et $\ \overrightarrow{NP}$ sont colinéaires et calculer $k.$
Exercice 5
Sur la figure ci-dessous, $I$ est le milieu de $[BC]\;,\ J\ $ et $\ K$ sont les points tels que :
$$\overrightarrow{AJ}=\dfrac{1}{3}\overrightarrow{AC}\ \text{ et }\ \overrightarrow{AK}=\dfrac{1}{4}\overrightarrow{BC}$$
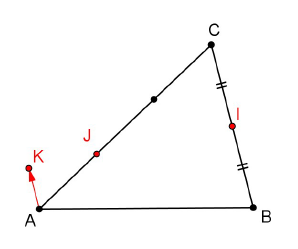
On considère le repère $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC}).$
Calculer les coordonnées de $I\;,\ J\ $ et $\ K$ puis prouver que $I\;,\ J\ $ et $\ K$ sont alignés.
Barycentre de deux points
Exercice 6
$A\ $ et $\ B$ sont deux points tels que $AB=6\;cm$. Construire (s'il existe) le barycentre de $(A\;;\ \alpha)\;,\ (B\;;\ \beta)$ dans chacun des cas suivants :
1) $\alpha=4\;,\quad \beta=-1$
2) $\alpha=2\;,\quad \beta=1$
3) $\alpha=2\;,\quad \beta=-2$
4) $\alpha=\dfrac{1}{10}\;,\quad \beta=\dfrac{1}{5}$
Exercice 7
$A\ $ et $\ B$ sont deux points tels que $AB=9\;cm$. Construire (s'il existe) le barycentre de $(A\;;\ \alpha)\;,\ (B\;;\ \beta)$ dans chacun des cas suivants :
1) $\alpha=4\;,\quad \beta=5$
2) $\alpha=8\;,\quad \beta=-5$
3) $\alpha=-11\;,\quad \beta=2$
4) $\alpha=\dfrac{1}{2}\;,\quad \beta=-\dfrac{1}{2}$
5) $\alpha=-1\;,\quad \beta=-5$
6) $\alpha=0\;,\quad \beta=2011$
Exercice 8
Les points $A\ $ et $\ B$ sont donnés et $G$ est défini par la condition indiquée. Déterminer deux réels $\alpha$ et $\beta$ tel que $G$ soit le barycentre de $(A\;;\ \alpha)\;,\ (B\;;\ \beta).$
1) $\overrightarrow{AB}=2\overrightarrow{GB}$
2) $2\overrightarrow{GB}-3\overrightarrow{AB}=\vec{0}$
3) $2\overrightarrow{AB}+\overrightarrow{GA}-2\overrightarrow{GB}=\vec{0}$
Exercice 9
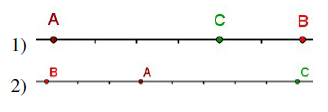
Pour les exercices suivants, les points $A\;,\ B\ $ et $\ C$ sont indiqués sur la figure. Dans les deux cas suivants, trouver deux réels $\alpha$ et $\beta$ tels que :
$\centerdot\ \ A$ soit le barycentre de $(B\;;\ \alpha)\;,\ (C\;;\ \beta)$
$\centerdot\ \ B$ soit le barycentre de $(A\;;\ \alpha)\;,\ (C\;;\ \beta)$
$\centerdot\ \ C$ soit le barycentre de $(A\;;\ \alpha)\;,\ (B\;;\ \beta)$
Barycentre de trois points
Exercice 10
$ABC$ est un triangle de centre de gravité $G\;,\ G'$ est le symétrique de $G$ par rapport au milieu de $[BC].$
1) Prouver que $G$ est le milieu de $[G'A]$
2) Justifier que :
$$\overrightarrow{G'G}=\overrightarrow{G'B}+\overrightarrow{G'C}$$
3) Exprimer $\overrightarrow{G'A}$ en fonction de $\overrightarrow{G'B}\ $ et $\ \overrightarrow{G'C}$ puis en déduire que $G'$ est un barycentre de $A\;,\ B\ $ et $\ C$ affectés de coefficients que l'on précisera.
Exercice 11
$ABC$ est un triangle. Construire (s'il existe) le barycentre de $(A\;;\ \alpha)\;,\ (B\;;\ \beta)\;,\ (C\;;\ \gamma)$ dans chacun des cas suivants :
1) $\alpha=3\;,\quad \beta=2\;,\quad \gamma=1$
2) $\alpha=1\;,\quad \beta=-1\;,\quad \gamma=-3$
3) $\alpha=2\;,\quad \beta=1\;,\quad \gamma=2$
4) $\alpha=\dfrac{1}{2}\;,\quad \beta=-\dfrac{1}{3}\;,\quad \gamma=-\dfrac{1}{6}$
Exercice 12
$ABC$ est un triangle; $I$ est le barycentre de $(A\;,\ 2)\;,\ (B\;,\ 1)\;,\ J$ celui de $(B\;,\ 1)\;,\ (C, -2)\ $ et $\ G$ le barycentre de $(A\;,\ 2)\;,\ (B\;,\ 1)\;,\ (C\;,\ -2).$ Le but de l'exercice est de localiser $G$ à l'intersection de deux droites.
1) Quel théorème permet de justifier l'alignement de $A\;,\ J\ $ et $\ G$, puis celui de $C\;,\ I\ $ et $\ G\ ?$
2) En déduire que $G$ est à l'intersection de $(AJ)$ et de $(CI).$ Placer alors $G.$
3) Démontrer que $(BG)\ $ et $\ (AC)$ sont parallèles.
Exercice 13
$ABC$ est un triangle. Les points $I\ $ et $\ J$ sont repérés sur la figure ci-dessous, dont les graduations sont régulières. $G$ est le milieu de $[CI].$
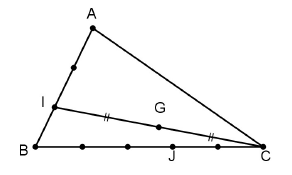
Le but de l'exercice est de montrer que $A\;,\ G\ $ et $\ J$ sont alignés.
1) Exprimer $I$ comme un barycentre de $A$ et de $B$, puis $J$ comme un barycentre de $B$ et de $C.$
2) On note $G'$ le barycentre de $(A\;,\ 1)\;,\ (B\;,\ 2)\;,\ (C\;,\ 3).$ Quel théorème permet de justifier que $G'$ est le milieu de $[IC]\ ?$ En déduire que $G'=G.$
3) Démontrer que $A\;,\ G\ $ et $\ J$ sont alignés.
Exercice 14
$ABC$ est un triangle de centre de gravité $G$. Le but de l'exercice est de déterminer l'ensemble $\delta$ des points $M$ du plan tels que le vecteur $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$ est colinéaire à $\overrightarrow{AB}.$
1) Exprimer $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$ en fonction de $\overrightarrow{MG}.$
2) Justifier l'affirmation : "Dire que M appartient à $\Delta$ équivaut à dire que $\overrightarrow{GM}$ est colinéaire à $\overrightarrow{AB}$"
3) En déduire $\Delta$ et le construire.
Exercice 15
Pour les exercices suivants, trouver trois réels $\alpha\;,\ \beta\ $ et $\ \gamma$ tels que $G$ soit barycentre de $(A\;,\ \alpha)\;,\ (B\;,\ \beta)\;,\ (C\;,\ \gamma)$
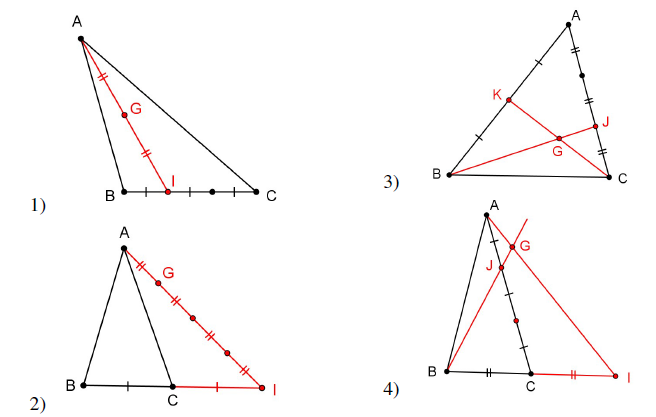
Barycentre de n points
Exercice 16
Pour les exercices suivants, justifier de l'existence du barycentre G, puis le construire.
1) $ABCD$ est un rectangle et $G$ le barycentre de $(A\;,\ -1)\;,\ (B\;,\ 2)\;,\ (C\;,\ 2)\;,\ (D\;,\ 2).$
2) $ABCD$ est un parallélogramme et $G$ le barycentre de $(A\;,\ 2)\;,\ (B\;,\ -3)\;,\ (C\;,\ 2)\;,\ (D\;,\ 2).$
3) $ABCD$ est un quadrilatère et $G$ le barycentre de $(A\;,\ -1)\;,\ (B\;,\ 3)\;,\ (C\;,\ 2)\;,\ (D\;,\ 2).$
Exercice 17
La figure ci-dessous indique une construction de barycentre $G$ de $(A\;,\ 1)\;,\ (B\;,\ 3)\;,\ (C\;,\ 1)\;,\ (D\;,\ 1).$ Justifier cette construction.
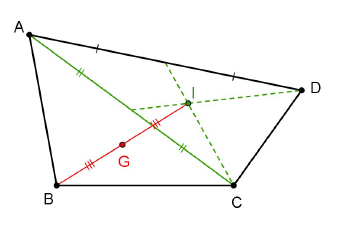
Exercice 18
$ABCD$ est un rectangle, construire le barycentre $G$ de $(A\;,\ \alpha)\;,\ (B\;,\ \beta)\;,\ (C\;,\ \gamma)\;,\ (D\;,\ \delta)$ dans chacun des cas suivants :
1) $\alpha=-2\;,\quad \beta=3\;,\quad \gamma=1\;,\quad \delta=1$
2) $\alpha=-3\;,\quad \beta=2\;,\quad \gamma=1\;,\quad \delta=-3$
3) $\alpha=-\dfrac{1}{8}\;,\quad \beta=\dfrac{3}{8}\;,\quad \gamma=\dfrac{1}{4}\;,\quad \delta=\dfrac{1}{2}$
Coordonnées du barycentre
Exercice 19
1) Placer les points $A(1\;,\ 3)\ $ et $\ B(2\;,\ 1).$
2) Calculer les coordonnées des points $M$, barycentre de $(A\;,\ -1)\;,\ (B\;,\ 3)\ $ et $\ N.$ barycentre de $(A\;,\ 2)\;,\ (B\;,\ -1).$
3) Calculer les coordonnées du milieu $I\ $ de $\ [AB].$
4) Trouver le réel $k$ tel que $\overrightarrow{MI}=k\overrightarrow{MN}$
5) En déduire deux réels $\alpha\ $ et $\ \beta$ tels que $I$ soit le barycentre de $(M\;,\ \alpha)\;,\ (N\;,\ \beta)$
Exercice 20
1) Placer les points $A(2\;,\ 1)\;,\ B(-1\;,\ 4)\ $ et $\ C(-3\;,\ -2).$
2) Calculer les coordonnées du centre de gravité $G$ du triangle $ABC.$
3) Calculer les coordonnées de $G'$, barycentre de $(A\;,\ -2)\;,\ (B\;,\ 3)\;,\ (C\;,\ 1).$
4) Les points $O\;,\ G\ $ et $\ G'$ sont-ils alignés ?
Ensemble de point
Exercice 21
$[AB]$ est un segment de longueur 5 cm. On se propose de trouver l'ensemble $\Gamma$ des points $M$ tels que :
$$||2\overrightarrow{MA}+3\overrightarrow{MB}||=10$$
1) On pose $G$ le barycentre de $(A\;,\ 2)\;,\ (B\;,\ 3).$
Réduire la somme $2\overrightarrow{MA}+3\overrightarrow{MB}.$
2) En déduire la nature de $\Gamma.$ Construire alors $\Gamma$
Exercice 22
$ABC$ est un triangle rectangle isocèle en $A$ tel que $AB=4\;cm.$ On se propose de trouver l'ensemble $\Gamma$ des points $M$ tels que :
$$||-\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=4$$
1) On pose $G$ le barycentre de $(A\;,\ -1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 2).$
Réduire la somme $-\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}$
2) En déduire la nature de $\Gamma.$
3) Montrer que $\Gamma$ passe par le point $C.$ Construire $G$ puis $\Gamma$
Exercice 23
$ABC$ est un triangle équilatéral de coté $5\;cm.$
1) Construire $G$, barycentre de $(A\;,\ 1)\;,\ (B\;,\ -1)\;,\ (C\;,\ 1)$, et prouver que $ABCG$ est un losange.
2) Quel est l'ensemble $\Gamma$ des points $M$ tels que :
$$||\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}||=\dfrac{5\sqrt{3}}{2}$$
3) Vérifier que le milieu de $[AC]$ appartient à $\Gamma.$ Tracer $\Gamma.$
Exercice 24
$ABC$ est un triangle rectangle en $A\;,\ I$ est le milieu de $[BC]\;,\ \Gamma$ est le cercle de centre $A$ passant par $I.\ G$ est le point diamétralement opposé à $I.$
1) Prouver que le point $G$ est le barycentre de $(A\;,\ 4)\;,\ (B\;,\ -1)\;,\ (C\;,\ -1).$
2) Trouver deux réels $b\ $ et $\ c$ tels que $A$ est le barycentre de $(G\;,\ 2)\;,\ (B\;,\ b)\;,\ (C\;,\ c).$
3) Quel est l'ensemble des points $M$ du plan tels que :
$$||2\overrightarrow{MG}+\overrightarrow{MB}+\overrightarrow{MC}||=2||\overrightarrow{BC}||$$
Centre d'inertie
Exercice 25
Pour chacune des plaques homogènes suivantes, construire le centre d'inertie.
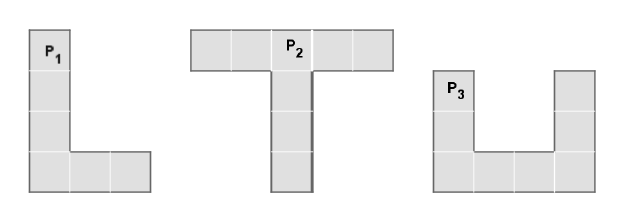
Exercice 26
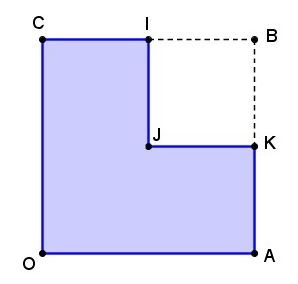
Une plane homogène $P$ est constituée par un carré $OABC$ de côté $8\;cm$ dont on a retiré le carré $BIJK$ de côté $4\;cm.$
Trouver la position du centre d'inertie de la plaque par deux méthodes.
Exercice 27
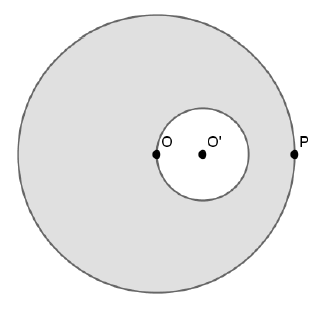
Une rondelle a la forme d'un disque évidé suivant le schéma ci-dessous pour lequel $OP=3OO'.$
1) Trouver la position du centre d'inertie $I$ de la rondelle évidée.
2) On note $M$ la masse de la rondelle évidée. Quelle masse m doit-on placer en $P$ afin que l'ensemble constitué de la rondelle et du point "massique" $P$ ait $O$ pour centre d'inertie ?
Exercice 28
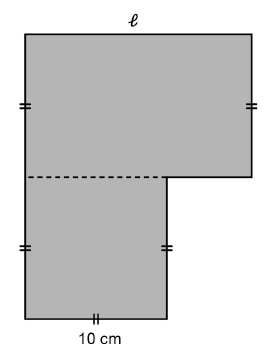
On considère une plaque homogène composée d'un carré de côté $10\;cm$ surmonté d'un rectangle de hauteur $10\;cm$ et de longueur $\ell$ (exprimée en $cm$) tel que $l\geq 10$ (figure ci-dessous)
Déterminer la longueur maximale $\ell_{max}$ pour laquelle la plaque reste en équilibre sur la base $[AB].$

Commentaires
Anonyme (non vérifié)
mar, 09/24/2019 - 15:44
Permalien
Oui j l veut
Dje cheikh (non vérifié)
lun, 01/25/2021 - 23:13
Permalien
Connaissance
Diallo (non vérifié)
sam, 02/20/2021 - 23:09
Permalien
la corrections
Tomy (non vérifié)
lun, 11/08/2021 - 08:33
Permalien
Math
Boubacarsiddy D... (non vérifié)
dim, 01/07/2024 - 02:40
Permalien
Demande d'aide
Boubacarsiddy D... (non vérifié)
dim, 01/07/2024 - 02:43
Permalien
Demande d'aide
Abdoulaye cissé (non vérifié)
mer, 10/16/2019 - 12:24
Permalien
Td
Diakhate (non vérifié)
dim, 10/27/2019 - 22:55
Permalien
Intéressant et très utile
Saliou ngom (non vérifié)
sam, 11/09/2019 - 01:23
Permalien
Math
Anonyme (non vérifié)
dim, 01/26/2020 - 13:32
Permalien
Bon document
Anonyme (non vérifié)
sam, 05/23/2020 - 11:16
Permalien
BIEN
Anonyme (non vérifié)
mar, 06/09/2020 - 06:02
Permalien
Je comptend pas
Antoine Moustap... (non vérifié)
mar, 09/15/2020 - 11:08
Permalien
Révision
Antoine Moustap... (non vérifié)
mar, 09/15/2020 - 11:09
Permalien
Révision
Makaila (non vérifié)
ven, 12/18/2020 - 19:02
Permalien
Résolution des exercices
Anonyme (non vérifié)
mer, 02/03/2021 - 15:07
Permalien
J veux la correction
Anonyme (non vérifié)
mar, 03/23/2021 - 14:55
Permalien
très bon document
Anonyme (non vérifié)
jeu, 04/15/2021 - 23:34
Permalien
correction svp
Anonyme (non vérifié)
jeu, 04/15/2021 - 23:39
Permalien
fayefallou066@gmail.com
JOD (non vérifié)
mar, 08/17/2021 - 23:28
Permalien
fayefallou066@gmail.com
Anonyme (non vérifié)
lun, 09/13/2021 - 15:48
Permalien
Salut! Un grand merci à vous
kante (non vérifié)
dim, 01/16/2022 - 23:26
Permalien
etudes
kante (non vérifié)
dim, 01/16/2022 - 23:31
Permalien
etudes
Anonyme (non vérifié)
ven, 01/21/2022 - 20:50
Permalien
good
Bamba Diouf (non vérifié)
ven, 04/01/2022 - 14:58
Permalien
Correction des exercices de maths et physique chimie en 1ere s2
Bamba Diouf (non vérifié)
ven, 04/01/2022 - 15:01
Permalien
Correction des exercices de maths et physique chimie en 1 été S2
Téby Wilfried (non vérifié)
dim, 12/04/2022 - 01:39
Permalien
Barycentre ou encore ;
Bikouta (non vérifié)
sam, 01/06/2024 - 13:15
Permalien
Corrigé au complet de cette fiche sur les barycentres
Ajouter un commentaire