Bac Maths, S Centres étrangers 12 mai 2022
Sujet 2
Épreuve d'enseignement de spécialité
Le sujet propose $4$ exercices
Le candidat choisit $3$ exercices parmi les $4$ exercices et ne doit traiter que ces $3$ exercices.
Chaque exercice est noté sur $7$ points $($le total sera ramené sur $20$ points$).$
Les traces de recherche, même incomplètes ou infructueuses, seront prises en compte.
Exercice 1 Thème : Fonction exponentielle
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Une réponse incorrecte, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée
1. Soit $f$ la fonction définie sur $\mathbb{R}$ par $$f(x)=\dfrac{x}{\mathrm{e}^{x}}$$
On suppose que $f$ est dérivable sur $\mathbb{R}$ et on note $f'$ sa fonction dérivée.
a. $f'(x)=\mathrm{e}^{x}$
b. $f'(x)=x\mathrm{e}^{-x}$
c. $f'(x)=(1-x)\mathrm{e}^{-x}$
d. $f'(x)=(1+x)\mathrm{e}^{-x}$
2. Soit $f$ une fonction deux fois dérivable sur l'intervalle $[-3\ ;\ 1].$
On donne ci-dessous la représentation graphique de sa fonction dérivée seconde $f''.$
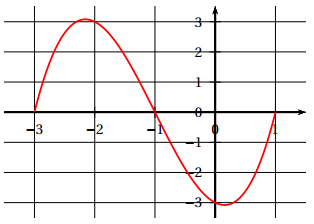
On peut alors affirmer que :
a. La fonction $f$ est convexe sur l'intervalle $[-1\ ;\ 1]$
b. La fonction $f$ est concave sur l'intervalle $[-2\ ;\ 0]$
c. La fonction $f'$ est décroissante sur l'intervalle $[-2\ ;\ 0]$
d. La fonction $f'$ admet un maximum en $x=-1$
3. On considère la fonction $f$ définie sur $\mathbb{R}$ par :$$f(x)=x^{3}\mathrm{e}^{-x^{2}}$$
Si $F$ est une primitive de $f$ sur $\mathbb{R}$,
a. $F(x)=-\dfrac{1}{6}\left(x^{3}+1\right)\mathrm{e}^{-x^{2}}$
b. $F(x)=-\dfrac{1}{4}x^{4}\mathrm{e}^{-x^{2}}$
c. $F(x)=-\dfrac{1}{2}\left(x^{2}+1\right)\mathrm{e}^{-x^{2}}$
d. $F(x)=x^{2}\left(3-2x^{2}\right)\mathrm{e}^{-x^{2}}$
4. Que vaut :$$\lim\limits_{\;x\longrightarrow+\infty}\dfrac{\mathrm{e}^{x}+1}{\mathrm{e}^{x}-1}$$
a. $-1$
b. $1$
c. $+\infty$
d. n'existe pas
5. On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\mathrm{e}^{2x+1}.$
La seule primitive $F$ sur $\mathbb{R}$ de la fonction $f$ telle que $F(0)=1$ est la fonction :
a. $x\mapsto\;2\mathrm{e}^{2x+1}-2\mathrm{e}+1$
b. $x\mapsto\;2\mathrm{e}^{2x+1}-\mathrm{e}$
c. $x\mapsto\dfrac{1}{2}\mathrm{e}^{2x+1}-\dfrac{1}{2}\mathrm{e}+1$
d. $x\mapsto\mathrm{e}^{x^{2}+x}$
Dans un repère, on a tracé ci-dessous la courbe représentative d'une fonction $f$ définie et deux fois dérivable sur $[-2\ ;\ 4]$
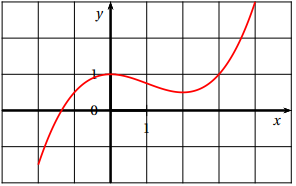
Parmi les courbes suivantes, laquelle représente la fonction $f''$, dérivée seconde de $f$ ?
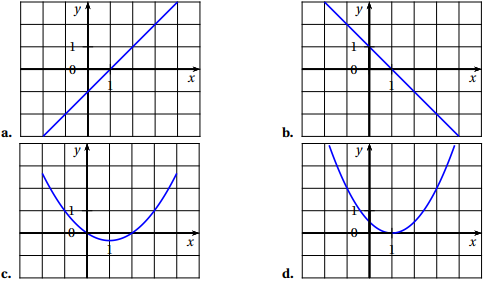
Exercice 2 Thèmes : Fonction logarithme et suite
Soit $f$ la fonction définie sur l'intervalle $]0\ ;\ +\infty[$ par
$$f(x)=x\ln(x)+1$$
On note $\mathcal{C}_{f}$ sa courbe représentative dans un repère du plan.
1. Déterminer la limite de la fonction $f$ en $0$ ainsi que sa limite en $+\infty.$
2. a. On admet que $f$ est dérivable sur $]0\ ;\ +\infty[$ et on notera $f'$ sa fonction dérivée.
Montrer que pour tout réel $x$ strictement positif :$$f'(x)=1+\ln(x).$$
b. En déduire le tableau de variation de la fonction $f$ sur $]0\ ;\ +\infty[.$
On y fera figurer la valeur exacte de l'extremum de $f$ sur $]0\ ;\ +\infty[$ et les limites.
c. Justifier que pour tout $x\in]0\ ;\ 1[\;,\ f(x)\in\,]0\ ;\ 1[.$
3. a. Déterminer une équation de la tangente $(\mathcal{T})$ à la courbe $\mathcal{C}_{f}$ au point d'abscisse $1.$
b. Étudier la convexité de la fonction $f$ sur $]0\ ;\ +\infty[.$
c. En déduire que pour tout réel $x$ strictement positif :$$f(x)\geq x$$
4. On définit la suite $\left(u_{n}\right)$ par son premier terme $u_{0}$ élément de l'intervalle $]0\ ;\ 1[$ et pour tout entier naturel $n$ :$$u_{n+1}=f\left(u_{n}\right)$$
a. Démontrer par récurrence que pour tout entier naturel $n$, on a : $0<u_{n}<1.$
b. Déduire de la question 3. c. la croissance de la suite $\left(u_{n}\right).$
c. En déduire que la suite $\left(u_{n}\right)$ est convergente.
Exercice 3 Thème : Géométrie dans l'espace
L'espace est muni d'un repère orthonormé $\left(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}\right).$
On considère les points
$A(3\ ;\ -2\ ;\ 2)$,
$B(6\ ;\ 1\ ;\ 5)$,
$C(6\ ;\ -2\ ;\ -1)$
et $D(0\ ;\ 4\ ;\ -1).$
On rappelle que le volume d'un tétraèdre est donné par la formule :
$$V=\dfrac{1}{3}\mathfrak{A}\times h$$
où $A$ est l'aire de la base et $h$ la hauteur correspondante.
1. Démontrer que les points $A$, $B$, $C$ et $D$ ne sont pas coplanaires.
2. a. Montrer que le triangle $ABC$ est rectangle.
b. Montrer que la droite $(AD)$ est perpendiculaire au plan $(ABC).$
c. En déduire le volume du tétraèdre $ABCD.$
3. On considère le point $H(5 ;\ 0\ ;\ 1).$
a. Montrer qu'il existe des réels $\alpha$ et $\beta$ tels que $\overrightarrow{BH}=\alpha\overrightarrow{BC}+\beta\overrightarrow{BD}.$
b. Démontrer que $H$ est le projeté orthogonal du point $A$ sur le plan $(BCD).$
c. En déduire la distance du point $A$ au plan $(BCD).$
4. Déduire des questions précédentes l'aire du triangle $BCD.$
Exercice 4 Thème : Probabilités
Une urne contient des jetons blancs et noirs tous indiscernables au toucher.
Une partie consiste à prélever au hasard successivement et avec remise deux jetons de cette urne.
On établit la règle de jeu suivante :
$\bullet\ $un joueur perd 9 euros si les deux jetons tirés sont de couleur blanche ;
$\bullet\ $un joueur perd 1 euro si les deux jetons tirés sont de couleur noire ;
$\bullet\ $un joueur gagne 5 euros si les deux jetons tirés sont de couleurs différentes.
1. On considère que l'urne contient $2$ jetons noirs et $3$ jetons blancs.
a. Modéliser la situation à l'aide d'un arbre pondéré.
b. Calculer la probabilité de perdre $9€$ sur une partie.
2. On considère maintenant que l'urne contient $3$ jetons blancs et au moins deux jetons noirs mais on ne connait pas le nombre exact de jetons noirs.
On appellera N le nombre de jetons noirs.
a. Soit $X$ la variable aléatoire donnant le gain du jeu pour une partie.
Déterminer la loi de probabilité de cette variable aléatoire.
b. Résoudre l'inéquation pour $x$ réel :$$-x^{2}+30x-81>0$$
c. En utilisant le résultat de la question précédente, déterminer le nombre de jetons noirs que l'urne doit contenir afin que ce jeu soit favorable au joueur.
d. Combien de jetons noirs le joueur doit-il demander afin d'obtenir un gain moyen maximal ?
3. On observe $10$ joueurs qui tentent leur chance en effectuant une partie de ce jeu, indépendamment les uns des autres.
On suppose que $7$ jetons noirs ont été placés dans l'urne $($avec $3$ jetons blancs$).$
Quelle est la probabilité d'avoir au moins $1$ joueur gagnant $5$ euros ?

Commentaires
Assane Diémé (non vérifié)
lun, 10/30/2023 - 19:03
Permalien
je veux la correction des exercices
Ajouter un commentaire