Corrigé Bac Maths S1 S3 1er groupe 2010

1) Soit $M$ un point du plan.

 

on a 

$$\begin{eqnarray} M\in\mathcal{E} &\Leftrightarrow& MA=4MB \nonumber \\ &\Leftrightarrow& MA^{2}=16MB^{2} \nonumber \\ &\Leftrightarrow& MA^{2}-16MB^{2}=0 \nonumber \\ &\Leftrightarrow& (\overrightarrow{MA}-4\overrightarrow{MB})(\overrightarrow{MA}+4\overrightarrow{MB})=0 \nonumber \end{eqnarray}$$

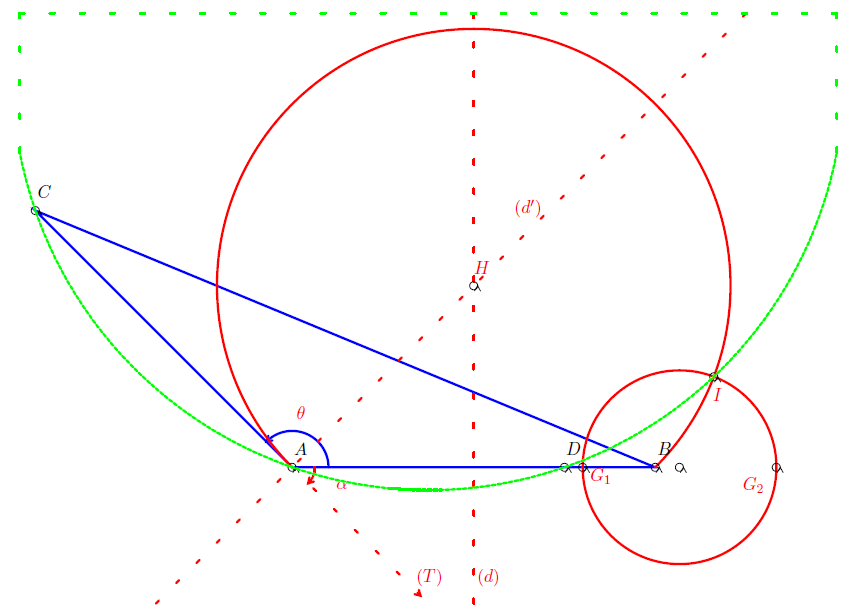
Faisons intervenir les barycentres $G_{1}$ et $G_{2}$ des systèmes $\{(A\;,\ 1)\;;\ (B\;,\ -4)\}\ $ et $\ \{(A\;,\ 1)\;;\ (B\;,\ 4)\}$ respectivement. Alors

$$M\in\mathcal{E}\;\Leftrightarrow\;\overrightarrow{G_{1}A}.\overrightarrow{G_{2}B}=0$$

$\mathcal{E}$ est donc le cercle de diamètre $[G_{1}G_{2}]$

 

2) L'ensemble $\mathcal{F}$ est l'arc capable défini par les points $A\;,\ B$ et l'angle $\theta=\dfrac{\pi}{4}.$

 

Soit $T$ l'unique demi droite d'origine $\theta$ telle que pour tout point $P$ de $T$, on a : $(\overrightarrow{AP}\;,\ \overrightarrow{AB})=\theta.$ Désignons par $H$ l'intersection de la médiatrice de $[AB]$ avec la perpendiculaire

à $T$ passant par $A$ et par $\mathcal{C}$ le cercle de centre $H$ et de rayon $HA.$

 

Alors $\mathfrak{F}$ est l'arc de $\mathcal{C}$ d'extrémités $A$ et $B$ tel que $\mathcal{F}$ et $T$ se trouvent dans des demi plans distincts de frontière la droite $(AB).$

 

3) a) $D$ étant l'image de $B$ par l'homothétie de centre $A$ et de rapport $\dfrac{3}{4}$, on a $\overrightarrow{AD}=\dfrac{3}{4}\overrightarrow{AB}.$

 

on en déduit que $\overrightarrow{DB}=\dfrac{1}{4}\overrightarrow{AB}.$

 

$C$ étant l'image de $B$ par la rotation de centre $A$ et d'angle $\dfrac{3}{4}\pi$, on a $AC=AB$ et $(\overrightarrow{AB}\;,\ \overrightarrow{AC})=\dfrac{3}{4}\pi.$

 

Dans le tableau suivant les points de la deuxième ligne sont les images par $s$ des points de la première ligne.

 

$$\begin{array}{|c|c|c|}\hline A & C & I \\ \hline B & D & I \\ \hline\end{array}$$

 

Le rapport de $s$ est $\dfrac{DB}{CA}=\dfrac{\dfrac{1}{4}AB}{CA}=\dfrac{1}{4}$ et son angle est modulo $2\pi\ :$

 

$$\begin{eqnarray} (\overrightarrow{AC}\;,\ \overrightarrow{BD}) &=& (\overrightarrow{AC}\;,\ -\overrightarrow{DB}) \nonumber \\ &=& \pi+(\overrightarrow{AC}\;,\ \overrightarrow{DB}) \nonumber \\ &=& \pi+(\overrightarrow{AC}\;,\ \overrightarrow{AB}) \nonumber \\ &=& \pi-\dfrac{3}{4}\pi=\dfrac{\pi}{4}\nonumber \end{eqnarray}$$

 

Le rapport de $s$ est $\dfrac{1}{4}$ et son angle est $\dfrac{\pi}{4}\;[2\pi]$

 

b) On a aussi $\dfrac{IB}{IA}=\text{ rapport de }s$ c'est à dire $\dfrac{IB}{IA}=4$ ou $I$ appartient à $\mathcal{E}$

 

Puis $(\overrightarrow{IA}\;,\ \overrightarrow{IB})=\text{ angle de }s\ $ c'est à dire $(\overrightarrow{IA}\;,\ \overrightarrow{IB})=\dfrac{\pi}{4}$ ou $I$ appartient à $\mathcal{F}.$

 

$I$ est donc le seul point d'intersection de $\mathcal{E}$ et de $\mathcal{F}.$

 

On a encore $(\overrightarrow{IC}\;,\ \overrightarrow{ID})=\text{ angle de }s\ $ c'est à dire $(\overrightarrow{IC}\;,\ \overrightarrow{ID})=\dfrac{\pi}{4}$

 

D'autre part $(\overrightarrow{AC}\;,\ \overrightarrow{AD})=(\overrightarrow{AC}\;,\ \overrightarrow{AB})=-\text{angle de }s\ $ c'est à dire $(\overrightarrow{AC}\;,\ \overrightarrow{AD})=-\dfrac{3\pi}{4}.$

 

On en déduit en faisant la différence $(\overrightarrow{IC}\;,\ \overrightarrow{ID})-(\overrightarrow{AC}\;,\ \overrightarrow{AD})=\pi$ c'est à dire $$(\overrightarrow{IC}\;,\ \overrightarrow{ID})=(\overrightarrow{AC}\;,\ \overrightarrow{AD})\;[\pi]$$

 

Donc les points $I\;,\ A\;,\ C$ et $D$ sont cocycliques, autrement dit $I$ appartient au cercle circonscrit au triangle $ACD.$

 

1) a) Pour que 193 soit premier, il faut et il suffit qu'il soit non divisible par tout nombre premier dont le carré est inférieur à 193. Ces nombres sont 2, 3, 5, 7, 11, 13 et aucun d'eux ne divise 193.

 

b) 193 étant premier, est premier avec tout entier naturel strictement plus petit, en particulier, il est premier avec 192.

 

Il suffit d'appliquer le petit théorème de Fermat avec $a=193\ $ et $\ p=192.$

 

2) a) Le couple $(x_{0}\;,\ y_{0})=(155\;,\ 67)$ est solution de $(E)$ parce que $83.155-192.67=1.$

 

b) Si $(x\;,\ y)$ est une solution de $(E)$ on peut écrire : $$\begin{array}{lcl} 83.x_{0}-192.y_{0} &=& 1 \\ 83.x-192.y &=& 1 \end{array}$$

 

Puis en faisant la différence

$$83.(x-x_{0})-192.(y-y_{0})=0$$

c'est à dire

$$83.(x-x_{0})=192.(y-y_{0})$$

 

Or 83 est premier avec 192 parce que l'équation $(E)$ a une solution (théorème de Bezout).

 

La relation précédente montre que 83 divise le produit $192.(y-y_{0})$ (en $x-x_{0}$ parties) ; comme il est premier avec 192, il divise $y-y_{0}$ (théorème de Gauss).

 

Donc il existe un entier $k$ tel que $y-y_{0}=83k$ soit $y=y_{0}+83k.$

 

La relation $83.x-192.y=1$ devient alors $83.x=192.(y_{0}+83k)+1=83.(x_{0}+192k)$ c'est à dire $x=x_{0}+192k.$

 

Ensuite on vérifie que n'importe quel couple du genre $(x_{0}+192k\;,\ y_{0}+83k)$ est bien une solution de $(E).$

 

L'ensemble des solutions de $(E)$ est $\{(155+192k\;,\ 67+83k)\;,\ k\in\mathbb{Z}\}$

 

3) On utilisera la propriété suivante : Si $a\;,\ b$ et $n$ sont des entiers tels que

$$a\equiv b[n]$$

alors pour tout entier naturel $k$ on a :

$$a^{k}\equiv b^{k}[n]$$

Posons $\mathcal{A}=\{0\;,\ \ldots\;,\ 192\}.$

 

Pour tout $a\in\mathcal{A}\;,\ f(a)\ $ et $\ g(a)$ sont les seuls éléments de $\mathcal{A}$ tels que :

$$f(a)=a^{83}[193]\qquad(1)$$

et $$g(a)=a^{155}[193]\qquad(2)$$

Puisque $g(a)$ appartient à $\mathcal{A}$, dans (2), on peut remplacer $a$ par $f(a)\ :$

$$g(f(a))=f(a)^{155}[193]$$

Dans (1) utilisons la propriété citée avec $k=155\ :$

$$f(a)^{155}=\left(a^{83}\right)^{155}[193]$$

On obtient alors par transitivité de $\equiv\ :$

$$g(f(a))\equiv a^{83\times 155}[193]\qquad(3)$$

 

a) Reprenons la relation $83.x_{0}+192.y_{0}=1$

 

qui s'écrit aussi : $83.x_{0}=1+192.y_{0}$

 

Cette relation permet d'avoir :

$$a^{83.x_{0}}=a^{1+192.y_{0}}=a\left(a^{192}\right)^{67}$$

 

Comme nous le savons déjà $a^{192}\equiv 1[193].$ Donc 

$$\begin{eqnarray} a^{83\times 155} &=& a^{83.x_{0}} \nonumber \\ &=& a^{1+192.y_{0}} \nonumber \\ &\equiv& a.1^{67}[193] \nonumber \end{eqnarray}$$

 

Finalement

$$a^{83\times 155}\equiv a[193]\qquad(4)$$

 

(3) et (4) entraînent par transitivité :

$$g(f(a))\equiv a[193]$$

 

$g(f(a))$ et $a$ sont des éléments de $\mathcal{A}$ équivalents modulo 193.

 

Nous allons monter qu'ils sont égaux.

 

$g(f(a))$ et $a$ sont des éléments de $\mathcal{A}$ entraîne $|g(f(a))-a|\leq 192$

 

$g(f(a))\equiv a[193]$ signifie il existe un entier $k$ tel que $g(f(a))-a=193k.$

 

On déduit de ces deux propriétés que $193|k|\leq 192$ c'est à dire $k=0$ ou $g(f(a))=a.$

 

Le même raisonnement montre que pour tout $a\in\mathcal{A}$, on a : $f(g(a))=a.$

 

Nous venons de démontrer que $f\circ g=g\circ f=I_{\mathcal{A}}$

Partie A

 

1) a) Dans (01), en dérivant la première équation et en remplaçant $v'$ par sa valeur tirée de la deuxième équation on obtient : $u''=v'=au.$ Cette dernière équation est équivalente à : $u''-au=0.$ La fonction $u$ est donc solution de (02).

 

De même, dans (01), en dérivant la deuxième équation et en remplaçant $u'$ par sa valeur tirée de de la première équation on obtient : $v''=au'=av.$ Cette dernière équation est équivalente à : $v''-av=0.$ La fonction $v$ est donc solution de (02), équation différentielle linéaire homogène du second ordre à coefficient constants.

 

b) l'équation caractéristique de (02) est $r^{2}-a=0.$

 

$\centerdot\ \ $ Si $a>0$ l'équation caractéristique a pour solutions $\sqrt{a}\ $ et $\ -\sqrt{a}.$ La solution générale de $y''-ay=0$ est donc $$y=\lambda\mathrm{e}^{\sqrt{a}t}+\mu\mathrm{e}^{-\sqrt{a}t}$$

$\lambda\ $ et $\ \mu$ constantes arbitraires.

 

La fonction $u$ étant solution de (02) est de la forme précédente.

 

La relation $v=u'$ donne alors $$v=\lambda\sqrt{a}\mathrm{e}^{\sqrt{a}t}-\mu\sqrt{a}\mathrm{e}^{-\sqrt{a}t}$$

 

La solution générale de (01) est donc

$$\begin{array}{lcl} u &=& \lambda\mathrm{e}^{\sqrt{a}t}+\mu\mathrm{e}^{-\sqrt{a}t} \\ v &=& \lambda\sqrt{a}\mathrm{e}^{\sqrt{a}t}-\mu\sqrt{a}\mathrm{e}^{-\sqrt{a}t}\;,\quad\lambda\;\text{ et }\;\mu\in\mathbb{R}\end{array}$$

 

$\centerdot\ \ $ Si $a<0$ l'équation caractéristique a pour solutions $\mathrm{i}\sqrt{-a}\ $ et $\ -\mathrm{i}\sqrt{-a}.$ La solution générale de $y''-ay=0$ est donc $$y=\lambda\cos\sqrt{-a}t+\mu\sin\sqrt{-a}t$$

$\lambda\ $ et $\ \mu$ constantes arbitraires.

 

La fonction $u$ étant solution de (02) est de la forme précédente.

 

La relation $v=u'$ donne alors $$v=-\lambda\sqrt{-a}\sin\sqrt{-a}t+\mu\sqrt{-a}\cos\sqrt{-a}t$$

 

La solution générale de (01) est donc

$$\begin{array}{lcl} u &=& \lambda\cos\sqrt{-a}t+\mu\sin\sqrt{-a}t \\ v &=& -\lambda\sqrt{-a}\sin\sqrt{-a}t+\mu\sqrt{-a}\cos\sqrt{-a}t\;,\quad\lambda\;\text{ et }\;\mu\in\mathbb{R} \end{array}$$

 

$\centerdot\ \ $ Si $a=0$ l'équation caractéristique a pour solutions 0. La solution générale de $y''-ay=0$ est donc $$y=\lambda t+\mu$$

$\lambda\ $ et $\ \mu$ constantes arbitraires.

 

La fonction $u$ étant solution de (02) est de la forme précédente.

 

La relation $v=u'$ donne alors $$v=\lambda$$

 

La solution générale de (01) est donc

$$\begin{array}{lcl} u &=& \lambda t+\mu \\ v &=& \lambda\end{array}\;,\quad\lambda\;\text{ et }\;\mu\in\mathbb{R}$$

 

2) Si $a=1$, il existe deux constantes $\lambda\ $ et $\ \mu$ telles que :

$$\begin{array}{lcl} u &=& \lambda\mathrm{e}^{t}+\mu\mathrm{e}^{-t} \\ v &=& \lambda\mathrm{e}^{t}-\mu\mathrm{e}^{-t}\end{array}$$

 

La relation $u(0)=3$ et $v(0)=0$ se traduit par

$$\begin{array}{lcl}\lambda+\mu &=& 3 \\ \lambda-\mu &=& 0\end{array}$$

 

Finalement

$$\begin{array}{lcl} u &=& \dfrac{3}{2}\left(\mathrm{e}^{t}+\mathrm{e}^{-t}\right) \\ \\ v &=& \dfrac{3}{2}\left(\mathrm{e}^{t}-\mathrm{e}^{-t}\right)\end{array}$$

 

Partie B

 

1) a) Un point $M$ de coordonnées $(x\;,\ y)$ appartient à $\Gamma$ si et seulement si $$\exists\;t\in\mathbb{R}\ :\ \begin{array}{lcl} x &=& \dfrac{3}{2}\left(\mathrm{e}^{t}+\mathrm{e}^{-t}\right) \\ \\ y &=& \dfrac{3}{2}\left(\mathrm{e}^{t}-\mathrm{e}^{-t}\right)\end{array}$$

En élevant au carré et en faisant la différence, on obtient

$$x^{2}-y^{2}=\dfrac{9}{4}\left(\mathrm{e}^{2t}+\mathrm{e}^{-2t}+2\right)-\dfrac{9}{4}\left(\mathrm{e}^{2t}+\mathrm{e}^{-2t}\right)-2=9$$

 

Par conséquent $\Gamma$ est bien contenue dans la courbe d'équation $x^{2}-y^{2}-9=0$

 

b) Pour construire $\Gamma$ il suffit de savoir que $\Gamma$ est la partie $C_{0}$ de la conique dont les points ont des coordonnées positives.

 

$\Gamma$ est contenue dans $C_{0}$ car pour tout réel $t\geq 0\;,\ x(t)$ et $y(t)$ sont positives.

 

Réciproquement, soit $M(x\;,\ y)$ un point de $C_{0}$ c'est à dire un point tel que :

$$\begin{array}{lcl} x &\geq& 0 \\ y &\geq& 0 \\ x^{2}-y^{2}-9 &=& 0\end{array}$$

 

et cherchons $t\in\mathbb{R}_{+}$ tel que

$$\begin{array}{lcl} x &=& \dfrac{3}{2}\left(\mathrm{e}^{t}+\mathrm{e}^{-t}\right) \\ \\ y &=& \dfrac{3}{2}\left(\mathrm{e}^{t}-\mathrm{e}^{-t}\right)\end{array}$$

La relation $x^{2}=y^{2}+9$ montre que $x$ est $\geq 3.$

 

En posant $s=\mathrm{e}^{t}$ on doit donc chercher un $s\geq 1$ tel que $x=\dfrac{3}{2}\left(s+\dfrac{1}{s}\right)$ c'est à dire

$$3s^{2}-2xs+3=0$$

 

Les racines de cette dernière équation sont

$$s_{1}=\dfrac{1}{3}(x+\sqrt{x^{2}-9})\quad\text{et}\quad s_{2}=\dfrac{1}{3}(x-\sqrt{x^{2}-9})$$

 

Les racines sont de même signe car leur produit est 1. La racine $s_{1}$ est $\geq 1$ ; en effet $s_{1}=\dfrac{1}{3}(x+\sqrt{x^{2}-9})\geq\dfrac{1}{3}x\geq 1.$

 

Donc la racine $s_{2}$ est $\leq 1.$

 

On prendra donc $s=s_{1}=\dfrac{1}{3}(x+\sqrt{x^{2}-9})$ c'est à dire $t=\ln\dfrac{1}{3}(x+\sqrt{x^{2}-9})$

 

Donc $C_{0}\subset\Gamma$

 

Finalement $C_{0}=\Gamma$

 

 

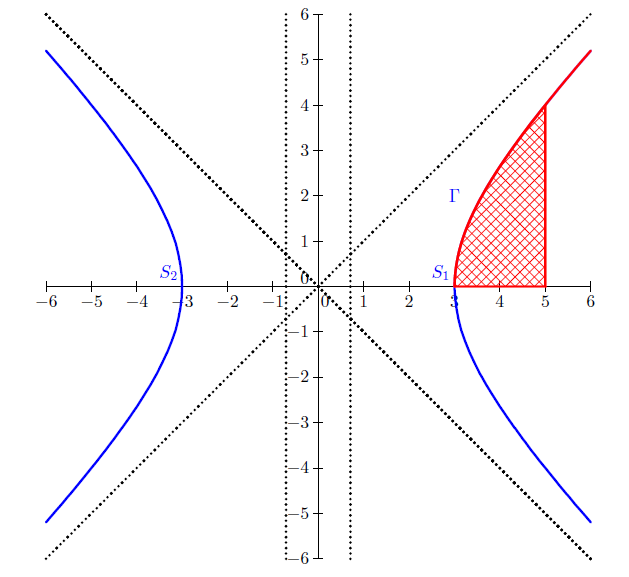
2) a) Un réel $x$ appartient à l'ensemble $D_{f}$ de définition de $f$ si et seulement si $x^{2}-9\geq$ c'est à dire $x\in\;]-\infty\;,\ 3]\cup[3\;,\ +\infty[.$

 

Donc $$\boxed{D_{f}=]-\infty\;,\ 3]\cup[3\;,\ +\infty[}$$

 

$\lim_{x\mapsto -\infty}f(x)=-\infty$

 

Quand $x\mapsto +\infty$ nous sommes en présence d'une indétermination de la forme $"+\infty-\infty".$

 

Pour lever cette indétermination, on peut écrire :

 

$$f(x)=x-\sqrt{x^{2}-9}=\dfrac{x^{2}-(x^{2}-9)}{x+\sqrt{x^{2}-9}}=\dfrac{9}{x+\sqrt{x^{2}-9}}$$

Donc $\lim_{x\mapsto +\infty}f(x)=0$

 

La fonction $f$ est dérivable sur $D_{f}=]-\infty\;,\ 3]\cup[3\;,\ +\infty[$ et $$\forall\;x\in\;D_{f}\;,\ f'(x)=1-\dfrac{x}{\sqrt{x^{2}-9}}$$

 

Si $x<-3$ , la dérivée est $>0.$

 

Si $x>3$, la dérivée est $<0$ car

 

$$f'(x)=\dfrac{\sqrt{x^{2}-9}-x}{\sqrt{x^{2}-9}}=\dfrac{-9}{\sqrt{x^{2}-9}(\sqrt{x^{2}-9}+x)}<0$$

 

On en déduit que la dérivée ne s'annule pas dans $\dot{D_{f}}.$

 

Au point 3, le taux d'accroissement est pour $h>0\ :$

$$\tau(h)=\dfrac{f(3+h)-f(3)}{h}=\dfrac{\sqrt{h^{2}+6h}}{h}=\sqrt{1+\dfrac{6}{h}}$$

 

Il a pour limite $+\infty$ quand $h$ tend vers $0^{+}.$ La fonction $f$ n'est donc pas dérivable à droite au point 3 et on peut ajouter qu'au point de $C_{f}$ dont l'abscisse est 3 il y a une demi-tangente verticale.

 

Raisonnement analogue au point -3 ; en ce point le taux d'accroissement est pour $h<0\ :$

$$\tau(h)=\dfrac{f(-3+h)-f(-3)}{h}=\dfrac{\sqrt{h^{2}-6h}}{h}=-\sqrt{1-\dfrac{6}{h}}$$

 

Il a pour limite $-\infty$ quand $h$ tend vers $0^{-}.$ La fonction $f$ n'est donc pas dérivable à gauche au point -3 et on peut ajouter qu'au point de $C_{f}$ dont l'abscisse est -3 il y a une demi-tangente verticale.

 

Voir le tableau de variation de $f$ en fin de document.

 

b) La fonction $f$ est continue et strictement décroissante dans l'intervalle $I.$ Sa restriction $\varphi$ à cet intervalle est donc une bijection de $I$ sur $J=f(I)=]\lim_{x\mapsto +\infty}f(x)\;,\ f(3)]=]0\;,\ 3]$

 

c) Soit $y\in\;J$ et cherchons $x\in\;I$ tel que $f(x)=y$

$$\begin{eqnarray} \forall\;y\in\;J\;,\ f(x)=y &\Leftrightarrow& y=x-\sqrt{x^{2}-9} \nonumber \\ &\Leftrightarrow& \left\lbrace\begin{array}{lcl} x-y &\geq& 0 \\ (x-y)^{2} &=& x^{2}-9 \end{array}\right. \nonumber \\ &\Leftrightarrow& \left\lbrace\begin{array}{lcr} x-y &\geq& 0 \\ -2xy+y^{2} &=& -9 \end{array}\right.\nonumber \\ &\Leftrightarrow& \left\lbrace\begin{array}{lcl} x-y &\geq& 0 \\ \\ x &=& \dfrac{y}{2}+\dfrac{9}{2y} \end{array} \right.\nonumber \end{eqnarray}$$

 

L'application réciproque de $\varphi$ est donc définie par $\forall\;y\in\;J\;,\ \varphi^{-1}(y)=\dfrac{y}{2}+\dfrac{9}{2y}=g(y)$

 

Remarque 

 

1. Une fois que l'on sait que $\varphi$ est bijective et puisque que la réciproque est donnée par l'énoncé, il suffit de vérifier que $\forall\;x\in\;J\;,\ g(x)\in\;I\;\text{ et }\;f\circ g(x)=x.$

 

L'étude des variations de $g$ montre bien que $g(J)=I.$

 

$$\forall\;y\in\;J\;,\ f\circ g(x)=g(x)-\sqrt{g(x)^{2}-9}=\dfrac{x}{2}+\dfrac{9}{2x}-\sqrt{\left(\dfrac{x}{2}+\dfrac{9}{2x}\right)^{2}-9}$$

 

$$\forall\;y\in\;J\;,\ f\circ g(x)=\dfrac{x}{2}+\dfrac{9}{2x}-\sqrt{\left(\dfrac{x}{2}-\dfrac{9}{2x}\right)^{2}}=\dfrac{x}{2}+\dfrac{9}{2x}-\left|\dfrac{x}{2}-\dfrac{9}{2x}\right|$$

 

Or $x\in\;]0\;,\ 3]\ \Rightarrow\ \dfrac{x}{2}-\dfrac{9}{2x}=\dfrac{x^{2}-9}{2x}=\dfrac{(x-3)(x+3)}{2x}\leq 0$ ; donc 

 

$$\forall\;y\in\;J\;,\ f\circ g(x)=\dfrac{x}{2}+\dfrac{9}{2x}-\left(-\dfrac{x}{2}+\dfrac{9}{2x}\right)=x$$

 

2. Si on n'a pas montré que $\varphi$ est bijective, il est nécessaire de vérifier que

$$\forall\;x\in\;J\;,\ g(x)\in\;I\;\text{ et }\;f\circ g(x)=x$$

et $$\forall\;x\in\;I\;,\ f(x)\in\;J\;\text{ et }\;g\circ f(x)=x$$

 

3) a) On a pour tout $\beta\in\;]0\;,\ 3[$

$$\int_{\beta}^{3}g(x)\mathrm{d}x=\left[\dfrac{x^{2}}{4}+\dfrac{9}{2}\ln|x|\right]_{\beta}^{3}$$

$$\int_{\beta}^{3}g(x)\mathrm{d}x=-\dfrac{\beta^{2}}{4}+\dfrac{9}{4}-\dfrac{9}{2}\ln\dfrac{\beta}{3}$$

 

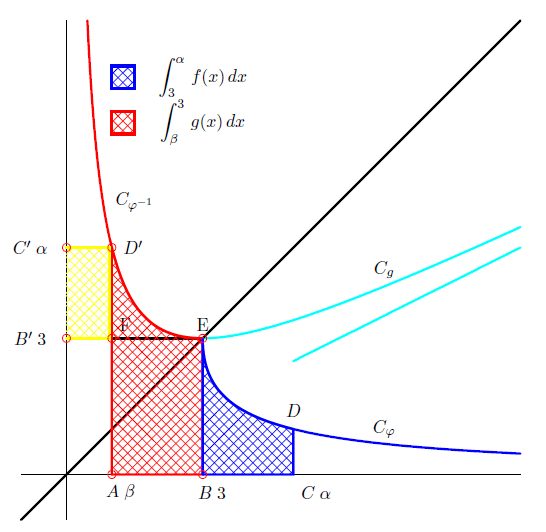
Les courbes $C_{\varphi}$ et $C_{\varphi^{-1}}$ étant symétriques par rapport à la première bissectrice, $\int_{3}^{\alpha}f(x)\mathrm{d}x$ représente aussi l'aire du domaine plan $\Delta_{1}$ délimité par les droites $(B'E)\;,\  (C'D')$ l'axe des ordonnées et la courbe $C_{\varphi^{-1}}.$

 

Soit $\Delta_{2}$ l'aire du rectangle $B'FD'C'$ et $\Delta_{3}$ l'aire du rectangle $ABEF.$ Alors :

$$\begin{eqnarray}\int_{3}^{\alpha}f(x)\mathrm{d}x &=& \int_{\beta}^{3}g(x)\mathrm{d}x +\Delta_{2}-\Delta_{3} \nonumber \\ &=& -\dfrac{\beta^{2}}{4}+\dfrac{9}{4}-\dfrac{9}{2}\ln\dfrac{\beta}{3}+\beta(\alpha-3)-3(3-\beta) \nonumber \\ &=& -\dfrac{\beta^{2}}{4}-\dfrac{27}{4}-\dfrac{9}{2}\ln\dfrac{\beta}{3}+\alpha\beta \nonumber \\ &=& -\dfrac{\beta^{2}}{4}-\dfrac{27}{4}-\dfrac{9}{2}\ln\dfrac{\beta}{3}+\left(\dfrac{\beta}{2}+\dfrac{9}{2\beta}\right)\beta \nonumber \end{eqnarray}$$

 

Finalement $$\int_{3}^{\alpha}f(x)\mathrm{d}x=\dfrac{\beta^{2}}{4}-\dfrac{9}{4}-\dfrac{9}{2}\ln\dfrac{\beta}{3}$$

 

b) Ici $\alpha=5$ donc $\beta$ est tel que $g(\beta)=5$ c'est à dire $\beta=f(5)=1.$

 

L'aire demandée est $$\mathcal{A}=\int_{3}^{\alpha}\sqrt{x^{2}-9}\mathrm{d}x$$ en unités d'aire.

$$\begin{eqnarray}\mathcal{A} &=& \int_{3}^{\alpha}\sqrt{x^{2}-9}\mathrm{d}x \nonumber \\ &=& -\int_{3}^{\alpha}f(x)\mathrm{d}x+\int_{3}^{\alpha}x\mathrm{d}x \nonumber \\ &=& -\dfrac{\beta^{2}}{4}+\dfrac{9}{4}-\dfrac{9}{2}\ln\dfrac{\beta}{3}+\dfrac{1}{2}\left[x^{2}\right]_{3}^{\alpha} \nonumber \\ &=& -\dfrac{\beta^{2}}{4}+\dfrac{9}{4}-\dfrac{9}{2}\ln\dfrac{\beta}{3}+\dfrac{1}{2}\alpha^{2} \nonumber \\ &=& -\dfrac{\beta^{2}}{4}-\dfrac{9}{4}+\dfrac{9}{2}\ln\dfrac{\beta}{3}+\dfrac{1}{2}\left(\dfrac{\beta}{2}+\dfrac{9}{2\beta}\right)^{2} \nonumber \\ &=& -\dfrac{\beta^{2}}{8}+\dfrac{81}{8\beta^{2}}+\dfrac{9}{2}\ln\dfrac{\beta}{3} \nonumber \end{eqnarray}$$

 

Et puisque $\beta=1\;,\ \mathcal{A}=10-\dfrac{9}{2}\ln 3$ unités d'aire.

 

Partie C

 

1) a) La fonction $g$ est définie et continue sur $\mathbb{R}^{*}$  et $\forall\;x\in\mathbb{R}^{*}\;,\ g'(x)=\dfrac{1}{2}\dfrac{x^{2}-9}{x^{2}}$

 

$$\lim_{x\mapsto +\infty}g(x)=+\infty\;,\ \lim_{x\mapsto -\infty}g(x)=-\infty\;,\ \lim_{x\mapsto 0^{+}}g(x)=+\infty\;,\ \lim_{x\mapsto 0^{-}}g(x)=-\infty$$

Voir le tableau de variation de $g$ en fin de document.

 

Posons $K=[3\;,\ +\infty[.$ Le tableau de variation de $g$ montre que $g(K)=K.$

 

Démontrons par récurrence que $\forall\;n\in\mathbb{N}\;,\ u_{n}>3.$

 

La propriété est vrai au rang 0 par ce que $u_{0}=5>3.$

 

Supposons que la propriété soit vraie jusqu'à un rang $n$, en particulier $u_{n}>3$ c'est à dire $u_{n}\in\;K.$ Alors $u_{n+1}=g(u_{n})\in\;g(K)=K.$

 

Par conséquent la propriété est vraie pour tout $n.$

 

La fonction $g$ étant strictement croissante dans K, son taux d'accroissement est strictement positif dans $K.$ Donc, puisque pour tout $n\in\mathbb{N}^{*}\;,\ u_{n}$ et $u_{n-1}$ appartiennent à $K$, on a : $\dfrac{g(u_{n})-g(u_{n-1})}{u_{n}-u_{n-1}}$ est strictement positif c'est à dire $\dfrac{u_{n+1}-u_{n}}{u_{n}-u_{n-1}}>0$

 

b) Les réels $u_{n+1}-u_{n}$ et $u_{n}-u_{n-1}$ ayant même signe, la suite $(u_{n+1}-u_{n})$ garde un signe constant. Cela signifie que la suite $(u_{n})$ est monotone.

 

Le signe de $u_{n+1}-u_{n}$ est alors celui de $u_{1}-u_{0}=\dfrac{5}{2}+\dfrac{9}{10}-5=-\dfrac{13}{5}<0.$

 

La suite $(u_{n})$ est strictement décroissante.

 

La suite $(u_{n})$ étant décroissante et minorée par 3, a une limite $\ell$ supérieure à 3.

 

c) Puisque la fonction $g$ est continue dans $K$ (c'est une fonction rationnelle dont le dénominateur ne s'annule pas dans $K$) la relation $\forall\;n\in\mathbb{N}\;,\ g(u_{n})=u_{n+1}$ entraîne $g(\ell)=\ell$

 

c'est à dire $\ell=-3\ \text{ ou }\ 3.$ Donc 

$$\lim_{n\mapsto +\infty}u_{n}=3$$

 

2) a) Soient $n$ un entier naturel non nul et appliquons le théorème des accroissements finis $g$ dans l'intervalle $[3\;,\ u_{n-1}]\ :$ il existe un réel $x_{0}$ dans $[3\;,\ u_{n-1}]$ tel que $\dfrac{g(u_{n-1})-g(3)}{u_{n-1}-3}=g'(x_{0})$

 

c'est à dire $\dfrac{u_{n}-3}{u_{n-1}-3}=\dfrac{1}{2}-\dfrac{9}{2x_{0}^{2}}$

 

donc $\dfrac{u_{n}-3}{u_{n-1}-3}<\dfrac{1}{2}$

 

En faisant le produit membre à membre de $n=1$ à $n=p$ entier supérieur à 1 on obtient :

$$\prod_{n=1}^{n=p}\dfrac{u_{n}-3}{u_{n-1}-3}<\prod_{n=1}^{n=p}\dfrac{1}{2}$$

c'est à dire après simplification

$$\dfrac{u_{p}-3}{u_{0}-3}<\left(\dfrac{1}{2}\right)^{p}\quad\text{soit }\ u_{p}-3<\dfrac{1}{2^{p-1}}$$

Puisque $\lim_{p\mapsto +\infty}\dfrac{1}{2^{p-1}}=0\ \;\text{ et }\;\forall\;p\in\mathbb{N}^{*}\;,\ 0\leq u_{p}-3<\dfrac{1}{2^{p-1}}$

 

le théorème des gendarmes permet de conclure que $\lim_{p\mapsto +\infty}|u_{p}-3|=0$ c'est à dire

 

$$\lim_{p\mapsto +\infty}u_{p}=3$$

 

b) La relation $\forall\;p\in\mathbb{N}^{*}\;,\ 0\leq u_{p}-3<\dfrac{1}{2^{p-1}}$ montre que pour que $n$ soit tel que $u_{p}-3$ soit inférieur à $10^{-3}$, il suffit que $\dfrac{1}{2^{n-1}}\leq 10^{-3}$ c'est à dire $(n-1)\ln\dfrac{1}{2}\leq -3\ln 10\ $ ou $\ n\geq\dfrac{3\ln 10}{\ln 2}+1$

 

Finalement on peut prendre

$$n=E\left(\dfrac{3\ln 10}{\ln 2}+1\right)+1=11$$

 

3) a) Examinons d'abord le rapport $v_{n+1}$

$$\begin{eqnarray} v_{n+1} &=& \dfrac{u_{n+1}-3}{u_{n+1}+3} \nonumber \\ &=& \dfrac{\dfrac{u_{n}}{2}+\dfrac{9}{2u_{n}}-3}{\dfrac{u_{n}}{2}+\dfrac{9}{2u_{n}}+3} \nonumber \\ &=& \dfrac{u_{n}^{2}-6u_{n}+9}{u_{n}^{2}+6u_{n}+9} \nonumber \\ &=& \dfrac{(u_{n}-3)^{2}}{(u_{n}+3)^{2}} \nonumber \\ &=& v_{n}^{2} \nonumber \end{eqnarray}$$

En prenant le logarithme on trouve $\ln v_{n+1}=2\ln v_{n}$

 

La suite $(\ln v_{n})$ est donc géométrique de raison 2 et de $1^{er}$ terme $\ln v_{0}=\ln\dfrac{u_{0}-3}{u_{0}+3}=\ln\dfrac{2}{5}$

 

b) Par conséquent $\forall\;n\in\mathbb{N}\;,\ \ln v_{n}=2^{n}\ln v_{0}=\ln\left(\dfrac{2}{5}\right)^{2^{n}}$

 

Soit en posant $q=\dfrac{2}{5}\ :\ \forall\;n\in\mathbb{N}\;,\ v_{n}=q^{2^{n}}$

 

Tirons maintenant $u_{n}$ en fonction de $v_{n}\ :$

 

$$\begin{eqnarray} \forall\;n\in\mathbb{N}\;,\ v_{n}=\dfrac{u_{n}-3}{u_{n}+3} &\Leftrightarrow& u_{n}(1-v_{n})=3v_{n}+3 \nonumber \\ &\Leftrightarrow& u_{n}=3\dfrac{1+v_{n}}{1-v_{n}} \nonumber \end{eqnarray}$$

 

Donc $$\forall\;n\in\mathbb{N}\;,\ u_{n}=3\dfrac{1+q^{2^{n}}}{1-q^{2^{n}}}$$

 

Puisque $q$ appartient à $]0\;,\ 1[$, la suite $q^{2^{n}}$ a pour limite 0 quand $n$ tend vers $+\infty.$ Donc $$\lim_{n\mapsto +\infty}u_{n}=\lim_{n\mapsto +\infty}3\dfrac{1+q^{2^{n}}}{1-q^{2^{n}}}=3$$

 

$$\begin{array}{|c|lcccccr|} \hline x & -\infty & & -3 & & 3 & & +\infty \\ \hline f' & & + & | & & | & - & \\ \hline & & & -3 & & 3 & & \\ f &  &\nearrow & | & & | & \searrow & \\ &-\infty & & | & & | & & 0\\ \hline\end{array}$$

 

 

$$\begin{array}{|c|lcccccccr|}\hline x & -\infty & & -3 & & & & 3 & & +\infty \\ \hline g' & & + & | & - & || & - & | & + & \\ \hline & & & -3 & & -\infty & & | & & +\infty \\ g &  &\nearrow & | & \searrow & || & \searrow & | & \nearrow & \\ &-\infty & & | & & -\infty & & 3 & & \\ \hline \end{array}$$