Corrigé Bac Maths S2 1er groupe 2010

On considère le tableau ci-dessus indiquant les résultats d'une étude sur le nombre d'années $x$ en service des ouvriers d'une entreprise et de leur salaire $y$ en milliers de francs.

 

Notons $x_{i}$ les modalités de $x$ et $n_{i}$ l'effectif de $x_{i}$, avec $1\leq i\leq 6.$

 

Et Notons $y_{j}$ les modalités de $y$ et $n_{j}$ l'effectif de $y_{j}$, avec $1\leq j\leq 4.$

 

Soit $N$ l'effectif total

 

$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline x \backslash y &2&6&10&14&18&22& n_{j} \\ \hline 75&a&5&0&0&0&0& a+5 \\ \hline 125&0&7&1&0&2&0&10 \\ \hline 175&2&0&9&8&15&4&38 \\ \hline 225&0&1&0&3&b&1& b+5 \\ \hline n_{i}&a+2&13&10&11&b+17&5& N=a+b+58 \\ \hline\end{array}$$

 

1) Déterminons $a$ et $b$ pour que $\bar{x}=\dfrac{596}{59}\ $ et $\ \bar{y}=\dfrac{8450}{59}$

 

On sait que $\bar{x}=\dfrac{\sum_{1}^{6}n_{i}x_{i}}{N}\ $ et $\ \bar{y}=\dfrac{\sum_{1}^{4}n_{j}y_{j}}{N}$

 

Alors $$\bar{x}=\dfrac{2(a+2)+(6\times 13)+(10\times 10)+(14\times 11)+18(b+17)+(22\times 5)}{a+b+58}\ $$ et $\ \bar{y}=\dfrac{75(a+5)+(10\times 125)+(38\times 175)+225(b+5)}{a+b+58}$

 

Or $\bar{x}=\dfrac{596}{59}\ $ et $\ \bar{y}=\dfrac{8450}{59}$

 

D'où $$\bar{x}=\dfrac{2(a+2)+(6\times 13)+(10\times 10)+(14\times 11)+18(b+17)+(22\times 5)}{a+b+58}=\dfrac{596}{59}$$  

 

et $\bar{y}=\dfrac{75(a+5)+(10\times 125)+(38\times 175)+225(b+5)}{a+b+58}=\dfrac{8450}{59}$

 

On obtient ainsi le système suivant

 

$$\left\lbrace\begin{array}{lcl} 239a-233b &=& 4900 \\ 161a-193b &=& 2580 \end{array}\right.$$

D'où $a=40\ $ et $\ b=20$

 

On suppose $a=40\ $ et $\ b=20$ dans la suite. Et en associant à chaque valeur $x_{i}$ la moyenne $m_{i}$ de la série conditionnelle $(y/x=x_{i})$ ; on a obtenu le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|c|} \hline x &2&6&10&14&18&22 \\ \hline m&80&113&170&189&199&185 \\ \hline\end{array}$$

 

2) a) Calculons le coefficient de corrélation linéaire.

 

Déterminons d'abord les moyennes $\bar{x}$ et $\bar{m}$, les variances $V_{x}$ et $V_{y}$, les écarts-types $\sigma_{x}$ et $\sigma_{y}$, la covariance de $x$ et $y.$

 

Notons que la série statistique double $(x\;,\ m)$ est injective.

 

Ainsi on a 

$$\bar{x}=\dfrac{\sum_{1}^{6}x_{i}}{N}\;,\quad \bar{m}=\dfrac{\sum_{1}^{6}m_{i}}{N}$$

 

$$V_{x}=\dfrac{\sum_{1}^{6}x_{i}^{2}}{N}-\bar{x}^{2}\;,\quad V_{m}=\dfrac{\sum_{1}^{6}m_{i}^{2}}{N}-\bar{m}^{2}$$

 

$$\sigma_{x}=\sqrt{V_{x}}\;,\quad \sigma_{m}=\sqrt{V_{m}}\ \text{ et }\ cov(x\;,\ m)=\dfrac{\sum_{1}^{6}x_{i}m_{i}}{N}-\bar{x}\bar{m}$$

 

D'où $\bar{x}=12\;,\ \bar{m}=156\;,\ V_{x}\simeq 46.66\;,\ V_{m}\simeq 1933.33$

 

$\sigma_{x}\simeq 6.83\;,\ \sigma_{m}\simeq 43.96$ et $cov(x\;,\ m)\simeq 267.33$

 

Calculons maintenant le coefficient de corrélation linéaire $r.$

 

On sait que $r=\dfrac{cov(x\;,\ m)}{\sigma_{x}\sigma_{m}}$

 

d'où $r\simeq 0.89$

 

Puisque $r$ est proche de 1, il y a alors une forte corrélation entre $x$ et $m.$

 

b) La droite de régression de $m$ en $x$, notée $D_{m/x}$, a pour équation $m=ax+b$ avec $a=\dfrac{cov(x\;,\ m)}{V_{x}}$ et $b=\bar{m}-a\bar{x}$

 

D'où $$D_{m/x}\ :\ m=5.73x+87.25$$

 

c) Si $x=30$ alors $m\simeq 259.128$, d'où le salaire moyen d'un ouvrier ayant 30 ans d'ancienneté est sensiblement égal à 259130 F.

Le plan complexe est rapporté à un repère orthonormé $(O\;;\ \vec{u}\;,\ \vec{v})$ avec $||\vec{u}||=||\vec{v}||=2\;cm$ 

 

1) a) Résolvons dans $\mathbb{C}$ l'équation $z^{3}-1=0.$

 

On sait que $z^{3}-1=(z-1)(z^{2}+z+1)$

 

alors, $z^{3}-1=0$ si, et seulement si, $z^{3}-1=(z-1)(z^{2}+z+1)=0$

 

D'où, l'équation admet trois solutions données sous formes algébriques $$z_{1}=1\;,\quad z_{2}=\dfrac{-1-\mathrm{i}\sqrt{3}}{2}\;,\quad z_{3}=\dfrac{-1+\mathrm{i}\sqrt{3}}{2}$$

d'où, l'ensemble des solutions $S$ est : $$S=\left\{1\;,\ \dfrac{-1-\mathrm{i}\sqrt{3}}{2}\;,\ \dfrac{-1+\mathrm{i}\sqrt{3}}{2}\right\}$$

 

Donnons les formes trigonométriques de ces équations :

$$z_{1}=\cos 0+\mathrm{i}\sin 0\;,\quad z_{2}=\cos\dfrac{4\pi}{3}+\mathrm{i}\sin\dfrac{4\pi}{3}\;,\quad z_{3}=\cos\dfrac{2\pi}{3}+\mathrm{i}\sin\dfrac{2\pi}{3}$$

 

b) Résolvons l'équation $z^{3}=8$ sachant que $2^{3}=8$

 

$z^{3}=8$ est équivalant à $\left(\dfrac{z}{2}\right)^{3}=1$ ce qui implique d'après 1) a) que $$\dfrac{z}{2}=1\quad\text{ou}\quad  \dfrac{z}{2}=\dfrac{-1-\mathrm{i}\sqrt{3}}{2}\quad\text{ou}\quad \dfrac{z}{2}=\dfrac{-1+\mathrm{i}\sqrt{3}}{2}$$

 

D'où : $$z=2\quad\text{ou}\quad  z=-1-\mathrm{i}\sqrt{3}\quad\text{ou}\quad z=-1+\mathrm{i}\sqrt{3}$$

 

Ainsi, l'ensemble des solutions de l'équation $z^{3}=8$ est $$S_{1}=\{2\;;\ -1-\mathrm{i}\sqrt{3}\;;\ -1+\mathrm{i}\sqrt{3}\}$$  

 

2) a) Plaçons dans le repère les points $A\;,\ B$ et $C$ d'affixes respectives $$z_{A}=2\;,\quad  z_{B}=-1-\mathrm{i}\sqrt{3}\quad\text{et}\ z_{C}=-1+\mathrm{i}\sqrt{3}$$

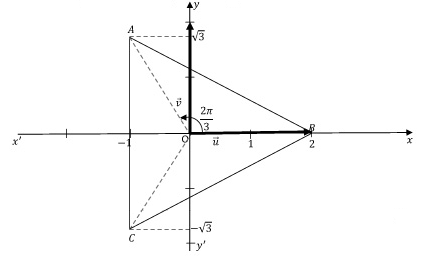
b) Calculons le module et un argument de $\dfrac{z_{A}-z_{B}}{z_{C}-z_{B}}.$

 

Nous avons $\dfrac{z_{A}-z_{B}}{z_{C}-z_{B}}=\dfrac{-1-\mathrm{i}\sqrt{3}}{2}$

 

d'où : $$\left|\dfrac{z_{A}-z_{B}}{z_{C}-z_{B}}\right|=1\quad\text{et}\quad arg\left(\dfrac{z_{A}-z_{B}}{z_{C}-z_{B}}\right)=-\dfrac{\pi}{3}$$

 

$(\overrightarrow{BC}\;,\ \overrightarrow{BA})=-\dfrac{\pi}{3}$, d'où le triangle $ABC$ est équilatéral.

 

2) a) Soit $f$ la transformation qui associe à tout point $M(z)$ le point $M'(z')$ tel que $z'=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}z.$

 

Déterminons l'ensemble des points invariants par $f.$

 

Soit $\Omega(z_{O})$ tel que $f(\Omega)=\Omega$, alors $z_{O}=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}z_{O}.$ Ce qui implique que $z_{O}=0.$

 

d'où, $f$ admet comme point invariant $O.$

 

Ainsi, puisque $z'=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}z$ alors $z'-z_{O}=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}(z-z_{O}).$ Ce qui implique que pour tout $z$ différent de $z_{O}$ on a $\dfrac{z'-z_{O}}{z-z_{O}}=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}.$

 

D'où : $$\left|\dfrac{z'-z_{O}}{z-z_{O}}\right|=1\quad\text{et}\quad arg\left(\dfrac{z'-z_{O}}{z-z_{O}}\right)=\dfrac{2\pi}{3}$$

 

Ce qui est équivalent à : $\left\lbrace\begin{array}{rcl} OM' &=& OM \\ (\overrightarrow{OM}\;,\ \overrightarrow{OM}') &=& \dfrac{2\pi}{3} \end{array}\right.$

 

Donc, $M'$ est l'image de $M$ par une rotation.

 

La rotation a pour centre $O$ et pour angle $\dfrac{2\pi}{3}.$

 

b) Soit $A'$ est l'image de $A$ par $f$ alors  $z_{A'}=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}z_{A}=\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}\times 2\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}$

 

D'où, $z_{A'}=z_{C}$ ou $A'=C$

 

De même $f(C)=B.$

 

c) $f(A)=C$ et $f(C)=B$ on en déduit donc que la droite $(AC)$ est l'image de la droite $(BC)$ car l'image d'une droite par une rotation est une droite et que $B$ et $C$ appartiennent à la droite image.

On dispose d'un tiroir qui contient 5 paires de chaussures noires, 3 paires de chaussures vertes et 2 paires de chaussures rouges, soit au total vingt chaussures. Toutes les paires sont de modèles différents.

 

1) On tire 2 chaussures au hasard.

 

Soit $\Omega$ l'univers des possibilités alors $card(\Omega)=C_{20}^{2}=190.$

 

a) Soit l'événement A : "tirer deux chaussures de la même couleur", alors l'événement A est "tirer deux chaussures noires ou deux chaussures vertes ou deux chaussures rouges"

 

D'où, $p(A)=\dfrac{C_{10}^{2}+C_{6}^{2}+C_{4}^{2}}{C_{20}^{2}}=\dfrac{66}{190}\simeq 0.35$

 

b) Soit l'événement B : "tirer un pied droit et un pied gauche"

 

Puisque dans le tiroir il y a dix pieds gauches et dix pieds droits alors, $p(B)=\dfrac{C_{10}^{1}\times C_{10}^{1}}{C_{20}^{2}}=\dfrac{100}{190}\simeq 0.52$

 

c) Soit l'événement C : "tirer les deux chaussures d'un même modèle"

 

Puisque toutes les chaussures sont de modèles différents alors il y a dix modèles.

 

On choisit un modèle parmi les dix et on prend les deux chaussures du modèle.

 

Donc $p(C)=\dfrac{C_{10}^{1}\times C_{2}^{2}}{C_{20}^{2}}=\dfrac{1}{19}\simeq 0.05$

 

2) Le tiroir ne contient maintenant qu'une paire de chaussures noires et une paire de chaussures rouges. On effectue un tirage successif et sans remise d'une chaussure du tiroir jusqu'à ce qu'il soit vide.

 

Soit la variable aléatoire $X$ égale au rang d'apparition de la deuxième chaussure noire.

 

a) Puisque $X$ est le rang d'apparition de la deuxième chaussure noire alors une première chaussure noire est déjà apparue donc la deuxième noire peut sortir au deuxième tirage ou au $3^{ème}$ ou au $4^{ème}$ et il ne peut pas y avoir plus de quatre tirages car il n'y a que deux paires dans le tiroir.

 

D'où, $X$ prend les valeurs 2, 3 ou 4.

 

Soit $\Omega$ l'univers alors $card(\Omega)=4!$

 

b) $(X=2)$ c'est obtenir dans cet ordre noire, noire, rouge, rouge.

 

Alors, $p(X=2)=\dfrac{2\times 1\times 2\times 1}{24}=\dfrac{1}{6}$

 

$(X=3)$ c'est obtenir dans cet ordre noire, rouge, noire, rouge ou rouge, noire, noire, rouge.

 

Alors, $p(X=3)=\dfrac{2(2\times 2\times 1\times 1)}{24}=\dfrac{1}{3}$

 

$(X=4)$ c'est obtenir dans cet ordre noire, rouge, rouge, noire ou rouge, noire, rouge, noire ou rouge, rouge, noire, noire.

 

Alors, $p(X=4)=\dfrac{2(2\times 2\times 1\times 1)+(2\times 1\times 2\times 1)}{24}=\dfrac{1}{2}$

 

c) Soit $E(X)$ l'espérance mathématique de $X$, alors 

$$\begin{eqnarray} E(X) &=& \sum_{1}^{3}a_{i}p(X=a_{i}) \nonumber \\ &=& \left(2\times\dfrac{1}{6}\right)+\left(3\times\dfrac{1}{3}\right)+\left(4\times\dfrac{1}{2}\right) \nonumber \\ &=& \dfrac{10}{3} \nonumber \end{eqnarray}$$

 

Sa variance $V(X)$ est :

$$\begin{eqnarray} V(X) &=& \sum_{1}^{3}a_{i}^{2}p(X=a_{i})-(E(X))^{2} \nonumber \\ &=& \left(4\times\dfrac{1}{6}\right)+\left(9\times\dfrac{1}{3}\right)+\left(16\times\dfrac{1}{2}\right)-\left(\dfrac{10}{3}\right)^{2} \nonumber \\ &=& \dfrac{5}{9}\simeq 0.55 \nonumber \end{eqnarray}$$

 

Son écart-type $\sigma_{X}$ est $\sqrt{V(X)}$, alors $$\sigma_{X}\simeq 0.74$$

Partie A

 

1) Étudions sur $\mathbb{R}$ le signe de $4\mathrm{e}^{2x}-5\mathrm{e}^{x}+1.$

 

Posons $y=\mathrm{e}^{x}$, considérons alors $4y^{2}-5y+1.$

 

Le trinôme $4y^{2}-5y+1=0$ admet deux racines  $y_{1}=\dfrac{1}{4}$ et $y_{2}=1$, d'où $4y^{2}-5y+1=4\left(y-\dfrac{1}{4}\right)(y-1)$ 

 

ou encore $4\mathrm{e}^{2x}-5\mathrm{e}^{x}+1=4\left(\mathrm{e}^{x}-\dfrac{1}{4}\right)(\mathrm{e}^{x}-1)$ avec $x_{1}=-2\ln 2$ et $x_{2}=0$ ses racines.

 

Son tableau de signe est :

 

$$\begin{array}{|c|lcccccr|}\hline x&-\infty& &-2\ln 2& &0& &+\infty \\ \hline\mathrm{e}^{x}-\tfrac{1}{4}& &-&|&+&|&+& \\ \hline\mathrm{e}^{x}-1& &-&|&-&|&+& \\ \hline 4\mathrm{e}^{2x}-5\mathrm{e}^{x}+1& &+&|&-&|&+& \\ \hline\end{array}$$

 

D'où, $4\mathrm{e}^{2x}-5\mathrm{e}^{x}+1\geq 0\ \text{ si }\ x\in\;]-\infty\;;\ -2\ln 2]\cup[0\;;\ +\infty[$

 

et $4\mathrm{e}^{2x}-5\mathrm{e}^{x}+1<0\ \text{ si }\ x\in\;]-2\ln 2\;;\ 0[$

 

2) Soit $\varphi$ la fonction définie par $\varphi(x)=\ln x-2\sqrt{x}+2.$

 

a)

 

$-$ Domaine de définition de $\varphi$

 

$\varphi$ est définie si, et seulement si, $x>0$ d'où le domaine de définition $D_{\varphi}$ de $\varphi$ est : $D_{\varphi}=]0\;;\ +\infty[$

 

$-$ Limites de $\varphi$ aux bornes de $D_{\varphi}$

$$\lim_{x\mapsto 0^{+}}\varphi(x)=-\infty\quad\text{et}\quad \lim_{x\mapsto +\infty}\varphi(x)=\lim_{x\mapsto +\infty}\sqrt{x}\left(\dfrac{2\ln\sqrt{x}}{\sqrt{x}}-2+\dfrac{2}{\sqrt{x}}\right)=-\infty$$

 

b) Étudions les variations de $\varphi$

 

$\varphi'(x)=\dfrac{1}{x}-\dfrac{1}{\sqrt{x}}=\dfrac{1-\sqrt{x}}{x}$, pour tout $x>0.$

 

D'où $$\begin{array}{rcl}\varphi'(x)=0 &\text{si}& x=1 \\ \varphi'(x)>0 &\text{si}& x\in\;]0\;;\ 1[ \\ \varphi'(x)<0 &\text{si}& x\in\;]1\;;\ +\infty[\end{array}$$

 

Dressons le tableau de variations de $\varphi$

$$\begin{array}{|c|lcccr|}\hline x&0& &1& &+\infty \\ \hline\varphi'(x)& &+&|&-& \\ \hline & & &0& & \\ \varphi& &\nearrow& &\searrow& \\ &-\infty& & & &-\infty \\ \hline\end{array}$$

 

c) D'après le tableau de variations $\varphi(x)$ admet un maximum en 1 et sa valeur maximale est 0.

 

D'où, pour tout $x\in\;D_{\varphi}\;,\ \varphi(x)\leq 0$

 

Partie B

 

Soit $f$ la fonction définie par :

$$f(x)=\left\lbrace\begin{array}{rcl} x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1} &\text{si}& x\leq 0 \\ \\ 1-x+\sqrt{x}\ln x &\text{si}& x>0 \end{array}\right.$$

 

$(\mathcal{C}_{f})$ sa courbe représentative dans un repère orthonormé d'unité graphique $2\;cm.$

 

1) a) Déterminons $D_{f}$ le domaine de définition de $f.$

 

$-$ Sur $]-\infty\;;\ 0]\;,\ f(x)=x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}$ est définie si, et seulement si, $2\mathrm{e}^{x}-1\neq 0$ c'est à dire $x\neq -\ln 2$

 

Donc, sur $]-\infty\;;\ 0]\ f$ est définie si $x\in\;]-\infty\;;\ -\ln 2[\cup]-\ln 2\;;\ 0]\quad(1)$

 

$-$ Sur $]0\;;\ +\infty[\ f(x)=1-x+\sqrt{x}\ln x$ est partout définie $\qquad(2)$

 

(1) et (2) impliquent que $$D_{f}=]-\infty\;;\ -\ln 2[\cup]-\ln 2\;;\ +\infty[$$

 

b) Calculons les limites aux bornes de $D_{f}$

 

$$\lim_{x\mapsto -\infty}f(x)=\lim_{x\mapsto -\infty}x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}=-\infty$$

 

$$\lim_{x\mapsto -\ln 2^{-}}f(x)=\lim_{x\mapsto -\ln 2^{-}}x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}=-\infty$$

 

$$\lim_{x\mapsto -\ln 2^{+}}f(x)=\lim_{x\mapsto -\ln 2^{+}}x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}=+\infty$$

 

$$\lim_{x\mapsto +\infty}f(x)=\lim_{x\mapsto +\infty}1-x+\sqrt{x}\ln x=\lim_{x\mapsto +\infty}x\left(\dfrac{1}{x}-1+\dfrac{2\ln\sqrt{x}}{\sqrt{x}}\right)=-\infty$$

 

Branches infinies 

 

$-\ \lim_{x\mapsto -\ln 2}f(x)=\lim_{x\mapsto -\ln 2}x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}=\infty$ alors la droite d'équation $x=-\ln 2$ est une asymptote verticale à la courbe $(\mathcal{C}_{f})$

 

$-$ On a $\lim_{x\mapsto -\infty}f(x)=-\infty$

 

calculons alors $\lim_{x\mapsto -\infty}\dfrac{f(x)}{x}$

 

$$\lim_{x\mapsto -\infty}\dfrac{f(x)}{x}=\lim_{x\mapsto -\infty}\dfrac{x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}}{x}=\lim_{x\mapsto -\infty}1+\dfrac{\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}}{x}=1\qquad(3)$$

 

Calculons $\lim_{x\mapsto -\infty}f(x)-x$

 

$$\lim_{x\mapsto -\infty}f(x)-x=\lim_{x\mapsto -\infty}x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}-x=\lim_{x\mapsto -\infty}\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}=0\qquad(4)$$

 

Conclusion : (3) et (4) impliquent que la droite $(\mathcal{D}_{1})$ d'équation $y=x$ est asymptote à la courbe $(\mathcal{C}_{f})$ au voisinage de $-\infty.$

 

$-$ De même on a $\lim_{x\mapsto +\infty}f(x)=+\infty$, calculons alors $\lim_{x\mapsto +\infty}\dfrac{f(x)}{x}$

 

$$\lim_{x\mapsto +\infty}\dfrac{f(x)}{x}=\lim_{x\mapsto +\infty}\dfrac{1-x+\sqrt{x}\ln x}{x}=\lim_{x\mapsto +\infty}\dfrac{1}{x}-1+\dfrac{2\ln\sqrt{x}}{\sqrt{x}}=-1\qquad(5)$$

 

Calculons $\lim_{x\mapsto +\infty}f(x)+x$

 

$$\lim_{x\mapsto +\infty}f(x)+x=\lim_{x\mapsto +\infty}1+\sqrt{x}\ln x=+\infty\qquad(6)$$

 

Conclusion : (5) et (6) impliquent que la courbe $(\mathcal{C}_{f})$ admet une branche infinie de direction asymptotique la droite $(\mathcal{D}_{2})$ d'équation $y=-x$ au voisinage de $+\infty.$

 

c) Position de $(\mathcal{C}_{f})$ par rapport à $(\mathcal{D}_{1})$ au voisinage de $-\infty.$

 

Au voisinage de $-\infty\ :\ f(x)-x>0\ \text{ si }\ \dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}>0$ 

 

c'est à dire $x\in\;]-\ln 2\;;\ 0]$

 

et $f(x)-x<0\ \text{ si }\ x\in\;]-\infty\;;\ -\ln 2[$

 

D'où, la courbe $(\mathcal{C}_{f})$ est en dessous de $(\mathcal{D}_{1})$ au voisinage de $-\infty.$

 

2) a) Étudions la continuité de $f$ en 0.

 

On a d'une part $f(0)=1$, d'autre part $$\lim_{x\mapsto 0^{-}}f(x)=\lim_{x\mapsto 0^{-}}x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}=1\quad\text{et}\quad\lim_{x\mapsto 0^{+}}f(x)=\lim_{x\mapsto 0^{+}}1-x+2\sqrt{x}\ln\sqrt{x}=1$$

 

d'où : $$\lim_{x\mapsto 0^{-}}f(x)=\lim_{x\mapsto 0^{+}}f(x)=f(0)=1$$

 

Donc, $f$ est continue en 0.

 

b) Étudions la dérivabilité de $f$ en 0 et interprétons graphiquement les résultats.

$$\begin{eqnarray}\lim_{x\mapsto 0^{-}}\dfrac{f(x)-f(0)}{x-0} &=& \lim_{x\mapsto 0^{-}}\dfrac{x+\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}-1}{x} \nonumber \\ &=& \lim_{x\mapsto 0^{-}}\dfrac{x(2\mathrm{e}^{x}-1)+\mathrm{e}^{x}-(2\mathrm{e}^{x}-1)}{x(2\mathrm{e}^{x}-1)} \nonumber \\ &=& \lim_{x\mapsto 0^{-}}\dfrac{x(2\mathrm{e}^{x}-1)-\mathrm{e}^{x}+1}{x(2\mathrm{e}^{x}-1)} \nonumber \\ &=& \lim_{x\mapsto 0^{-}}1-\dfrac{\mathrm{e}^{x}-1}{x(2\mathrm{e}^{x}-1)} \nonumber \\ &=& \lim_{x\mapsto 0^{-}}1-\dfrac{\dfrac{\mathrm{e}^{x}-1}{x}}{2\mathrm{e}^{x}-1} \nonumber \\ &=& 0 \nonumber \end{eqnarray}$$  

 

D'où, $f$ est dérivable à gauche de 0 et son nombre dérivé à gauche de 0, $f'_{g}(0)$, est $f'_{g}(0)=0.$

 

La courbe représentative de $f\;,\ (\mathcal{C}_{f})$ admet une tangente horizontale à gauche du point d'abscisse 0.

 

De même 

$$\begin{eqnarray}\lim_{x\mapsto 0^{+}}\dfrac{f(x)-f(0)}{x-0} &=& \lim_{x\mapsto 0^{+}}\dfrac{1-x+\sqrt{x}\ln x-1}{x} \nonumber \\ &=& \lim_{x\mapsto 0^{+}}\dfrac{-x+\sqrt{x}\ln x}{x} \nonumber \\ &=& \lim_{x\mapsto 0^{+}}-1+\dfrac{2\ln\sqrt{x}}{\sqrt{x}} \nonumber \\ &=& -\infty \nonumber \end{eqnarray}$$  

 

D'où, $f$ n'est pas dérivable à droite de 0. 

 

La courbe représentative de $f\;,\ (\mathcal{C}_{f})$ admet une tangente verticale à droite du point d'abscisse 0.

 

3) Calculons la dérivée de $f(x)$

$$f'(x)=\left\lbrace\begin{array}{lcl}\dfrac{4\mathrm{e}^{2x}-5\mathrm{e}^{x}+1}{(2\mathrm{e}^{x}-1)^{2}} &\text{si}& x\in\;]-\infty\;;\ -\ln 2[\cup]-\ln 2\;;\ 0] \\ \\ \dfrac{1}{2\sqrt{x}}(\ln x-2\sqrt{x}+2) &\text{si}& x\in\;]0\;;\ +\infty[\end{array}\right.$$

 

Signe de la dérivée

 

Sur $]-\infty\;;\ -\ln 2[\cup]-\ln 2\;;\ 0]\;,\ f'(x)$ a le même signe que $4\mathrm{e}^{2x}-5\mathrm{e}^{x}+1.$

 

Et sur $]0\;;\ +\infty[\;,\ f'(x)$ a le même signe que $\ln x-2\sqrt{x}+2.$

 

Donc d'après la partie A, $f'(x)\leq 0\ \text{ sur }[-2\ln 2\;;\ -\ln 2[\cup]-\ln 2\;;\ +\infty[$

 

et $f'(x)\geq 0\ \text{ sur }]-\infty\;;\ -2\ln 2]$

 

Tableau de variations de $f$

$$\begin{array}{|c|lcccccccr|}\hline x&-\infty& &-2\ln 2& &-\ln 2& &0& &+\infty \\ \hline f'(x)& &+&|&-&||&-& &-& \\ \hline & & &(-1/2-2\ln 2)& &+\infty& & & & \\ f& &\nearrow& &\searrow&||& &\searrow & & \\ &-\infty& & & &-\infty& & & &-\infty \\ \hline\end{array}$$

 

4) Construction de la courbe, des asymptotes et des tangentes

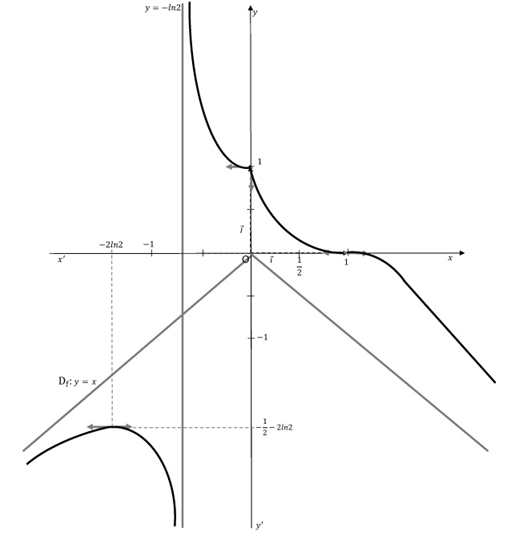
5) Calculons l'aire $\mathcal{A}$, en $cm^{2}$, du domaine du plan délimité par la droite d'équation $y=x$, la courbe et les droites d'équations $x=-\ln 8$ et $x=-\ln 4$

$$\begin{eqnarray}\mathcal{A} &=& \int_{-\ln 8}^{-\ln 4}\left(x-x-\dfrac{\mathrm{e}^{x}}{2\mathrm{e}^{x}-1}\right)\mathrm{d}x\times 4\;cm^{2} \nonumber \\ &=& \left[-\dfrac{1}{2}\ln|2\mathrm{e}^{x}-1|\right]_{-\ln 8}^{-\ln 4}\times 4\;cm^{2} \nonumber \\ &=& 2\ln\dfrac{3}{2}\;cm^{2} \nonumber \end{eqnarray}$$

Auteur : Mouhamadou Ka