1. Expression littérale de l'énergie potentielle du skieur en A.
Ep(z)=mgz+cte
Alors, Ep(ZB)=mgzB+cte or, Ep(ZB)=0
Donc,
mgzB+cte=0⇒mg×0+cte=0⇒cte=0⇒Ep(z)=mgz
Ainsi, EpA(Z)=mgzA or, zA=dsinα
Par suite, EpA(z)=mgdsinα
A.N : EpA(z)=115×10×103×sin26.0∘=5.0⋅105
D'où, EpA(z)=5.0⋅105J
2. Expression littérale de l'énergie cinétique du skieur en B.
Le système est conservatif, la conservation de l'énergie mécanique s'écrit :
EcB=12mv2B
A.N : EcB=12×115×50.52=1.5⋅105
D'où, EcB=1.5⋅105J
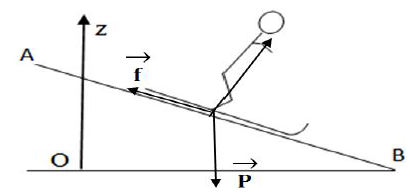
3. Nommons les forces appliquées au système {skieur + équipement} et représentons les sur un schéma.
Les forces qui exercent sur le système sont : →P; →R et →f éventuellement des forces de frottement
4. Expression du travail de chacune de ces forces.
WAB(→P)=→P⋅→AB=mgABsinα
WAB(→R)=→R⋅→AB=0J car →R⊥→AB
WAB(→f)=→f⋅→AB=−f×AB
5. Relation liant la variation d'énergie cinétique du système et le travail des différentes forces.
ΔEc=EcB−EcA=WAB(→P)+WAB(→R)+WAB(→f)
6. Sa vitesse au point B
ΔEc=EcB−EcA=WAB(→P)+WAB(→R)
Alors,
12mv2B−0=mgABsinα+0⇒v2B=2gABsinα⇒vB=√2gABsinα
A.N : vB=√2×10×103×sin26.0∘=93.6
D'où, vB=93.6m⋅s−1
7. Détermination de la valeur de ces frottements.
ΔEc=EcB−EcA=WAB(→P)+WAB(→R)+WAB(→f)
⇒ 12mv2B−0=mgABsinα+0−f×AB
⇒ f×AB=mgABsinα+0−12mv2B
⇒ f=m(gsinα−v2B2AB)
A.N : f=115(10sin26.0∘−50.522×103)=3.8⋅102
Ainsi, f=3.8⋅102N
Exercice 4
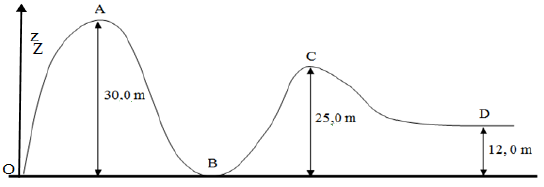
Calcul de la variation d'énergie potentielle de pesanteur du wagonnet passant :
1. de A à B
Choisissons l'axe z orienté vers le haut
Ep(z)=mgz+cte
ΔEp=EpB−EpA=mgzB+cte−(mgzA+cte)=mgzB−mgzA=mg(zB−zA)
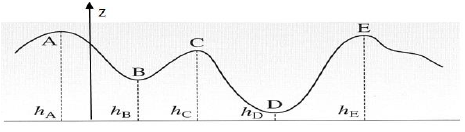
ΔEp=EpB−EpA=mg(hB−hA)=65×10×(15−10)⇒ΔEp=−65⋅102J
2. de B à C
ΔEp=EpC−EpB=mg(hC−hB)=65×10×(15−10)⇒ΔEp=−65⋅102J
3. de A à D
ΔEp=EpD−EpA=mg(hD−hA)=65×10×(5−20)⇒ΔEp=−97.5⋅102J
4. de A à E
ΔEp=EpE−EpA=mg(hE−hA)=65×10×(18−20)⇒ΔEp=−13⋅102J
Exercice 8
1. Expression de l'énergie potentielle de pesanteur du solide en en fonction de m, g, et z l'altitude du solide
Ep(z)=mgz+cte
Ep(z=0)=mg×0+cte=0⇒Ep=mgz
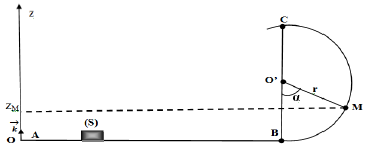
2. Déduction de l'énergie potentielle de pesanteur au point M en fonction de m, g, r, et α
EpM=mgzMor zM=r(1−cosα)⇒EpM=mgr(1−cosα)
3. Pour position C l'énergie potentielle de pesanteur est maximale, car zM=2r la position est maximale.
4. Expression de l'énergie mécanique du solide aux points suivants : A, B et C, sachant que le solide arrive au point C avec une vitesse vC.
EmA=EcA+EpA=12mv2A+mgzA=12mv2A+0⇒EmA=12mv2A
EmB=EcB+EpB=12mv2B+mgzB=12mv2B+0⇒EmB=12mv2B
EmC=EcC+EpC=12mv2C+mgzC=12mv2C+2mgr⇒EmC=12mv2C+2mgr
5. Montrons que le solide parcours le périmètre du boucle, on doit avoir Ec(A)>2mgr.
Les frottements sont négligés, l'énergie mécanique se conserve :
EmA=EmC=12mv2C+2mgr⇒EmA=EmA>2mgr
6. Calcul de la valeur de la vitesse initiale vA pour que le solide arrête au point C
EmA=EmC=12mv2C+2mgror vC=0⇒EmA=EcA=12mv2C=2mgr⇒v2C=4gr⇒vC=√4gr=√4×10×1.5⇒vC=7.7m⋅s−1


Commentaires
Lawani (non vérifié)
mar, 01/17/2023 - 19:25
Permalien
Être bon en physique et chimie
Lawani (non vérifié)
mar, 01/17/2023 - 19:27
Permalien
Être bon en physique et chimie
Klaranouba franklin (non vérifié)
ven, 05/19/2023 - 17:07
Permalien
Bah la correction du reste j'ai déjà traité
Marc tankou (non vérifié)
lun, 11/20/2023 - 16:26
Permalien
Approfondir mais connaissance en physique
Marc tankou (non vérifié)
lun, 11/20/2023 - 16:26
Permalien
Approfondir mais connaissance en physique
Mame diarra (non vérifié)
jeu, 12/28/2023 - 21:14
Permalien
Demande d'aide
Mame diarra (non vérifié)
jeu, 12/28/2023 - 21:14
Permalien
Demande d'aide
EDENLOUE (non vérifié)
lun, 10/28/2024 - 21:36
Permalien
Bonsoir Monsieur je ne
JBL (non vérifié)
lun, 02/24/2025 - 22:04
Permalien
Correction des exercices
Pages
Ajouter un commentaire