Corrigé Bac Maths S2 1er groupe 2007
Exercice 1 (04 points)
On considère dans $\mathbb{C}\;$, l'équation :
$$z^{3}-(3+2\mathrm{i})z^{2}+(1+4\mathrm{i})z+1-2\mathrm{i}=0$$
1) a) Déterminons la solution réelle de cette équation.
Soit $z=a$ la solution réelle de l'équation alors, on a :
$\begin{array}{rcl} a^{3}-(3+2\mathrm{i})a^{2}+(1+4\mathrm{i})a+1-2\mathrm{i}=0&\Rightarrow&a^{3}-3a^{2}-2\mathrm{i}a^{2}+a+4\mathrm{i}a+1-2\mathrm{i}=0\\\\&\Rightarrow&a^{3}-3a^{2}+a+1-(2a^{2}-4a+2)\mathrm{i}=0\end{array}$
Or, un nombre complexe est nul si, et seulement si, sa partie réelle et sa partie imaginaire sont toutes nulles.
Donc,
$\begin{array}{rcl} a^{3}-3a^{2}+a+1-(2a^{2}-4a+2)\mathrm{i}=0&\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \\ 2a^{2}-4a+2&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \\ 2(a^{2}-2a+1)&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \\ (a-1)^{2}&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \quad(1) \\ a&=&1\quad(2)\end{array}\right.\end{array}$
$a=1$ vérifie aussi l'équation $(1).$
Par conséquent, $1$ est la solution réelle cherchée.
b) Montrons que $\mathrm{i}$ est une solution de cette équation.
$\mathrm{i}$ est une solution de cette équation si, et seulement si, $\mathrm{i}$ vérifie l'équation
Dans l'équation, en remplaçant $z$ par $\mathrm{i}$, on obtient :
$\begin{array}{rcl}\mathrm{i}^{3}-(3+2\mathrm{i})\mathrm{i}^{2}+(1+4\mathrm{i})\mathrm{i}+1-2\mathrm{i}&=&-\mathrm{i}+3+2\mathrm{i}+\mathrm{i}-4+1-2\mathrm{i}\\\\&=&-3\mathrm{i}+3\mathrm{i}+6-6\\\\&=&0\end{array}$
Ce qui montre que $\mathrm{i}$ est une solution de l'équation :
$$z^{3}-(3+2\mathrm{i})z^{2}+(1+4\mathrm{i})z+1-2\mathrm{i}=0$$
c) Déterminons la troisième solution de cette équation.
On a : $z_{1}=1\ $ et $\ z_{2}=\mathrm{i}$ solutions de l'équation.
Soit $z_{3}$ la troisième solution de cette équation.
Alors, l'équation peut encore s'écrire de la forme :
$$(z-z_{1})(z-z_{2})(z-z_{3})$$
En développant, on obtient :
$\begin{array}{rcl} (z-z_{1})(z-z_{2})(z-z_{3})&=&z^{3}-z_{1}z^{2}-z_{2}z^{2}-z_{3}z^{2}+z_{1}z_{2}z+z_{1}z_{3}z+z_{2}z_{3}z-z_{1}z_{2}z_{3}\\\\&=&z^{3}-(z_{1}+z_{2}+z_{3})z^{2}+(z_{1}z_{2}+z_{1}z_{3}+z_{2}z_{3})z-z_{1}z_{2}z_{3}\end{array}$
Par suite,
$$z^{3}-(3+2\mathrm{i})z^{2}+(1+4\mathrm{i})z+1-2\mathrm{i}=z^{3}-(z_{1}+z_{2}+z_{3})z^{2}+(z_{1}z_{2}+z_{1}z_{3}+z_{2}z_{3})z-z_{1}z_{2}z_{3}$$
Ainsi,
$\begin{array}{rcl}\left\lbrace\begin{array}{rcl} (z_{1}+z_{2}+z_{3})&=&(3+2\mathrm{i})\\ (z_{1}z_{2}+z_{1}z_{3}+z_{2}z_{3})&=&(1+4\mathrm{i})\\-z_{1}z_{2}z_{3}&=&1-2\mathrm{i}\end{array}\right.&\Leftrightarrow&\left\lbrace\begin{array}{rcl} 1+\mathrm{i}+z_{3}&=&3+2\mathrm{i}\\ \mathrm{i}+z_{3}+\mathrm{i}z_{3}&=&1+4\mathrm{i}\\-\mathrm{i}z_{3}&=&1-2\mathrm{i}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} z_{3}&=&2+\mathrm{i}\\ \mathrm{i}+z_{3}+\mathrm{i}z_{3}&=&1+4\mathrm{i}\\-\mathrm{i}z_{3}&=&1-2\mathrm{i}\end{array}\right.\end{array}$
D'où, $z_{3}=2+\mathrm{i}$ est la troisième solution de l'équation.
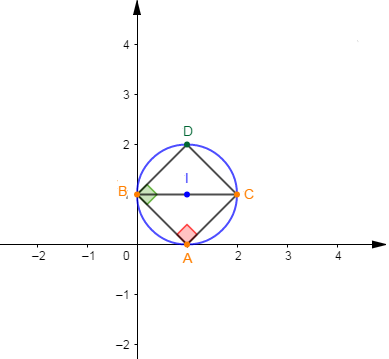
2) Soient les points $A\;,\ B\ $ et $\ C$ d'affixes respectives $1\;,\ \mathrm{i}\ $ et $\ 2+\mathrm{i}.$
a) Déterminons le module et un argument de $\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}.$
On a :
$\begin{array}{rcl} \left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|&=&\dfrac{|2+\mathrm{i}-1|}{|\mathrm{i}-1|}\\\\&=&\dfrac{|1+\mathrm{i}|}{|\mathrm{i}-1|}\\\\&=&\dfrac{\sqrt{2}}{\sqrt{2}}\\\\&=&1\end{array}$
Donc, $\boxed{\left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|=1}$
Soit :
$\begin{array}{rcl} arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)&=&arg\left(\dfrac{2+\mathrm{i}-1}{\mathrm{i}-1}\right)\\\\&=&arg(2+\mathrm{i}-1)-arg(\mathrm{i}-1)\\\\&=&arg(1+\mathrm{i})-arg(-1+\mathrm{i})\end{array}$
Or,
$1+\mathrm{i}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\mathrm{i}\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}.\mathrm{e}^{\mathrm{i}\tfrac{\pi}{4}}$
$-1+\mathrm{i}=\sqrt{2}\left(-\dfrac{\sqrt{2}}{2}+\mathrm{i}\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}.\mathrm{e}^{\mathrm{i}\tfrac{3\pi}{4}}$
Donc, $arg(1+\mathrm{i})=\dfrac{\pi}{4}\ $ et $\ arg(-1+\mathrm{i})=\dfrac{3\pi}{4}$
Par suite,
$\begin{array}{rcl} arg(1+\mathrm{i})-arg(-1+\mathrm{i})&=&\dfrac{\pi}{4}-\dfrac{3\pi}{4}\\\\&=&\dfrac{-2\pi}{4}\\\\&=&-\dfrac{\pi}{2}\end{array}$
D'où, $\boxed{arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)=-\dfrac{\pi}{2}\;[2\pi]}$
b) En déduisons la nature du triangle $ABC.$
On sait que : $\left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|=\dfrac{||\overrightarrow{AC}||}{||\overrightarrow{AB}||}\ $ et $\ arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)=(\overrightarrow{AB}\;,\ \overrightarrow{AC})\;[2\pi]$
Or, $\left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|=1$ donc, $||\overrightarrow{AC}||=||\overrightarrow{AB}||$
D'où, $AB=AC$
Aussi, $arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)=-\dfrac{\pi}{2}\;[2\pi]$ donc, $(\overrightarrow{AB}\;,\ \overrightarrow{AC})=-\dfrac{\pi}{2}\;[2\pi]$
Par conséquent, le triangle $ABC$ est rectangle isocèle en $A.$
c) Déterminons l'affixe du point $D$ image de $A$ par la rotation de centre $B$ et d'angle $\dfrac{\pi}{2}.$
Considérons l'expression complexe de la rotation d'angle $\dfrac{\pi}{2}$, de centre $B$ d'affixe $\mathrm{i}$ qui, à tout point $M$ d'affixe $z$ associe le point $M'$ d'affixe $z'.$
Soit alors :
$$z'-\mathrm{i}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}(z-\mathrm{i})$$
Donc, si $D$ est image de $A$ par cette rotation alors, son affixe $z_{D}$ sera donné par :
$\begin{array}{rcl} z_{D}-\mathrm{i}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}(z_{A}-\mathrm{i})&\Rightarrow&z_{D}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}(1-\mathrm{i})+\mathrm{i}\\\\&\Rightarrow&z_{D}=\mathrm{i}(1-\mathrm{i})+\mathrm{i}\\\\&\Rightarrow&z_{D}=\mathrm{i}+1+\mathrm{i}\\\\&\Rightarrow&z_{D}=2\mathrm{i}+1\end{array}$
Ainsi, $D$ est d'affixe $2\mathrm{i}+1$
d) Montrons que $A\;,\ B\;,\ C\ $ et $\ D$ sont sur un cercle de centre $I(1+\mathrm{i})$ et de rayon $r$ à déterminer.
On a : $A\;,\ B\;,\ C\ $ et $\ D$ cocycliques ou appartiennent à un même cercle si, et seulement si, $$\dfrac{(z_{D}-z_{B})(z_{A}-z_{C})}{(z_{A}-z_{D})(z_{B}-z_{C})}\quad \text{est réel}$$
Soit alors :
$\begin{array}{rcl}\dfrac{(z_{D}-z_{B})(z_{A}-z_{C})}{(z_{A}-z_{D})(z_{B}-z_{C})}&=&\dfrac{(2\mathrm{i}+1-\mathrm{i})(1-(2+\mathrm{i}))}{(1-(2\mathrm{i}+1))(\mathrm{i}-(2+\mathrm{i}))}\\\\&=&\dfrac{(\mathrm{i}+1)(-1-\mathrm{i})}{(-2\mathrm{i})(-2)}\\\\&=&\dfrac{-(\mathrm{i}+1)^{2}}{4\mathrm{i}}\\\\&=&\dfrac{-(-1+2\mathrm{i}+1)}{4\mathrm{i}}\\\\&=&\dfrac{(-2\mathrm{i})}{4\mathrm{i}}\\\\&=&-\dfrac{1}{2}\end{array}$
Ainsi, $\boxed{\dfrac{(z_{D}-z_{B})(z_{A}-z_{C})}{(z_{A}-z_{D})(z_{B}-z_{C})}=-\dfrac{1}{2}\in\mathbb{R}}$
Ce qui prouve que les points $A\;,\ B\;,\ C\ $ et $\ D$ sont sur un même cercle de centre $I(1+\mathrm{i})$
En effet, $ABC$ est rectangle isocèle en $A$ donc, le centre $I$ du cercle circonscrit à ce triangle est le milieu de l'hypoténuse $[BC].$
Ainsi, son affixe sera donné par :
$\begin{array}{rcl} z_{I}&=&\dfrac{z_{B}+z_{C}}{2}\\\\&=&\dfrac{\mathrm{i}+2+\mathrm{i}}{2}\\\\&=&\dfrac{2\mathrm{i}+2}{2}\\\\&=&\mathrm{i}+1\end{array}$
D'où, $\boxed{I(1+\mathrm{i})}$
Déterminons le rayon $r$ de ce cercle.
Soit :
$\begin{array}{rcl} r&=&||\overrightarrow{IA}||\\\\&=&|z_{\overrightarrow{IA}}|\\\\&=&|1-(1+\mathrm{i})|\\\\&=&|1-1-\mathrm{i}|\\\\&=&|-\mathrm{i}|\\\\&=&1\end{array}$
Donc, $\boxed{r=1}$
Exercice 2 (04 points)
1) On considère un dé cubique truqué dont les faces sont numérotées de $1\ $ à $\ 6.$
On note $p_{i}$ la probabilité d'apparition de la face numérotée $i.$ Les $p_{i}$ vérifient :
$$p_{1}=p_{2}\;;\quad p_{3}=p_{4}=2p_{1}\;;\quad p_{5}=p_{6}=3p_{1}$$
a) Montrons que $p_{1}=\dfrac{1}{12}.$
On sait que :
$$\sum_{i=1}^{6}p_{i}=1$$
Alors, $p_{1}+p_{2}+p_{3}+p_{4}+p_{5}+p_{6}=1$
Or, $p_{2}=p_{1}\;;\quad p_{3}=p_{4}=2p_{1}\;;\quad p_{5}=p_{6}=3p_{1}$
Donc, en remplaçant, on obtient :
$\begin{array}{rcl} p_{1}+p_{2}+p_{3}+p_{4}+p_{5}+p_{6}=1&\Rightarrow&p_{1}+p_{1}+2p_{1}+2p_{1}+3p_{1}+3p_{1}=1\\\\&\Rightarrow&12p_{1}=1\\\\&\Rightarrow&p_{1}=\dfrac{1}{12}\end{array}$
D'où, $\boxed{p_{1}=\dfrac{1}{12}}$
b) Montrons que la probabilité de l'événement $A$ : "obtenir $3$ ou $6$" est égale à $\dfrac{5}{12}.$
Soit $\{X=i\}$ l'événement "obtenir le numéro $i$" avec $p(\{X=i\})=p_{i}$
Donc, $A=\{X=3\}\cup\{X=6\}$ avec $\{X=3\}\ $ et $\ \{X=6\}$ deux événements incompatibles.
Par suite,
$\begin{array}{rcl} p(A)&=&p(\{X=3\}\cup\{X=6\})\\\\&=&p(\{X=3\})+p(\{X=6\})-p\underbrace{(\{X=3\}\cap\{X=6\})}_{=0}\\\\&=&p_{3}+p_{6}\quad\text{or, }\quad p_{3}=2p_{1}\ \text{ et }p_{6}=3p_{1}\\\\&=&5p_{1}\\\\&=&5\times\dfrac{1}{12}\\\\&=&\dfrac{5}{12}\end{array}$
D'où, $\boxed{p(A)=\dfrac{5}{12}}$
2) Un jeu d'adresse consiste à lancer le dé décrit ci-dessus puis à lancer une fléchette sur une cible fixe.
Si le joueur obtient $3$ ou $6$, il se place à $5\;m$ de la cible et lance la fléchette sur la cible ; à $5\;m\;$, la probabilité d'atteindre la cible est alors $\dfrac{3}{5}.$
Si l'événement $A$ n'est pas réalisé, il se place à $7\;m$ de la cible et lance la fléchette ; à $7\;m\;$, la cible est atteinte avec une probabilité égale à $\dfrac{2}{5}.$
On note $C$ l'événement : "la cible est atteinte".
a) Déterminons $p(C/A)\ $ et $\ p(C/\bar{A}).$
$p(C/A)$ est la probabilité d'atteindre la cible sachant que le joueur est à $5\;m.$
Ainsi, $\boxed{p(C/A)=\dfrac{3}{5}}$
$p(C/\bar{A})$ est la probabilité d'atteindre la cible sachant que le joueur est à $7\;m.$
D'où, $\boxed{p(C/\bar{A})=\dfrac{2}{5}}$
En déduisons que $p(C)=\dfrac{29}{60}.$
D'après la formule des probabilités totales, on a :
$\begin{array}{rcl} p(C)&=&p(C/A)p(A)+p(C/\bar{A})p(\bar{A})\quad\text{or, }p(\bar{A})=1-p(A)\\\\&=&\dfrac{3}{5}\times\dfrac{5}{12}+\dfrac{2}{5}\times\left(1-\dfrac{5}{12}\right)\\\\&=&\dfrac{15}{60}+\dfrac{14}{60}\\\\&=&\dfrac{29}{60}\end{array}$
Ainsi, $\boxed{p(C)=\dfrac{29}{60}}$
b) Déterminons $p(A/C).$
Soit : $p(A/C)=\dfrac{p(A\cap C)}{p(C)}$
Or, $p(A\cap C)=p(C/A)\times p(A)$ donc, en remplaçant, on obtient :
$\begin{array}{rcl} p(A/C)&=&\dfrac{p(A\cap C)}{p(C)}\\\\&=&\dfrac{p(C/A)\times p(A)}{p(C)}\\\\&=&\dfrac{\dfrac{3}{5}\times\dfrac{5}{12}}{\dfrac{29}{60}}\\\\&=&\dfrac{15}{60}\times\dfrac{60}{29}\\\\&=&\dfrac{15}{29}\end{array}$
Donc, $\boxed{p(A/C)=\dfrac{15}{29}}$
3) Le joueur dispose de $10$ fléchettes qu'il doit lancer une à une, de façon indépendante, dans les mêmes conditions que précédemment définies.
Calculons la probabilité pour qu'il atteigne la cible exactement $4$ fois.
En effet, nous sommes en présence d'un schéma de Bernoulli avec deux issues possibles : succès $(S)$ lorsque la cible est atteinte et échec $(E)$ lorsqu'elle ne l'est pas.
On a : $p(S)=p(C)\ $ et $\ p(E)=1-p(S)=1-p(C)$
Soit $Y$ la variable aléatoire de Bernoulli telle que : $\{Y=k\}$ est l'événement "obtenir $k$ succès sur $n$ épreuves.
Alors, on a :
$$p(\{Y=k\})=C_{n}^{k}.(p(S))^{k}.(p(E))^{n-k}$$
Donc, la probabilité d'atteindre la cible exactement $4$ fois ($4$ succès et $6$ échecs) lors des $10$ lancées sera donnée par :
$\begin{array}{rcl} p(\{Y=4\})&=&C_{10}^{4}.(p(S))^{4}.(p(E))^{6}\\\\&=&C_{10}^{4}\times(p(C))^{4}\times (1-p(C))^{6}\\\\&=&C_{10}^{4}\times\left(\dfrac{29}{60}\right)^{4}\times\left(1-\dfrac{29}{60}\right)^{6}\\\\&=&210\times\left(\dfrac{29}{60}\right)^{4}\times\left(\dfrac{31}{60}\right)^{6}\\\\&=&0.22\end{array}$
D'où, $\boxed{p(\{Y=4\})=0.22}$
Problème : (12 points)
I.
Soit $g$ la fonction définie sur $]0\;;\ +\infty[$ par :
$$g(x)=1+x+\ln x$$
1) Dressons le tableau de variation de $g.$
Soit $g'$ la fonction dérivée de $g$ alors, on a :
$$g'(x)=1+\dfrac{1}{x}$$
Donc, $\forall\;x\in\;]0\;;\ +\infty[\;;\ g'(x)>0$
Par suite, $g$ est strictement croissante sur $]0\;;\ +\infty[.$
Par ailleurs,
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}g(x)&=&\lim\limits_{x\rightarrow 0^{+}}(1+x+\ln x)\\\\&=&-\infty\end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}g(x)&=&\lim\limits_{x\rightarrow +\infty}(1+x+\ln x)\\\\&=&+\infty\end{array}$
D'où, le tableau de variations de $g$ suivant :
$$\begin{array}{|c|lcr|}\hline x&0&&+\infty\\ \hline g'(x)&|&+&\\ \hline&|&&+\infty\\g&|&\nearrow&\\&|-\infty&&\\ \hline \end{array}$$
2) Montrons qu'il existe un unique réel $\alpha$ solution de l'équation $g(x)=0.$
En effet, $g$ est continue et strictement croissante sur $]0\;;\ +\infty[$ donc, $g$ est une bijection de $]0\;;\ +\infty[$ sur $]-\infty\;;\ +\infty[$
Or, $0\in\;]-\infty\;;\ +\infty[$ donc, d'après le théorème de la bijection, il existe un unique réel $\alpha\in\;]0\;;\ +\infty[$ tel que $g(\alpha)=0.$
Vérifions que $\alpha$ appartient à $]0.2\;;\ 0.3[.$
Soit : $g(0.2)=1+0.2+\ln 0.2=-0.40\ $ et $\ g(0.3)=1+0.3+\ln 0.3=0.09$
Alors, $g(0.2)\times g(0.3)=-0.036<0$
Ainsi, $g$ est continue sur $]0.2\;;\ 0.3[\ $ et $\ g(0.2)\times g(0.3)<0.$
Donc, d'après le corollaire du théorème des valeurs intermédiaires il existe $\beta\in\;]0.2\;;\ 0.3[$ solution de l'équation $g(x)=0.$
Or, l'unique solution de cette équation est le réel $\alpha.$
Par conséquent, $\alpha=\beta.$ D'où, $\alpha$ appartient à $]0.2\;;\ 0.3[.$
3) En déduisons le signe de $g$ sur $]0\;;\ +\infty[.$
D'après les questions précédentes, on peut alors écrire :
$$g(]0\;;\ \alpha])=]-\infty\;;\ 0]\quad\text{ et }\quad g([\alpha\;;\ +\infty[)=[0\;;\ +\infty[$$
Ainsi,
$\centerdot\ \ g(x)\leq 0$ sur $]0\;;\ \alpha]$
$\centerdot\ \ g(x)\geq 0$ sur $[\alpha\;;\ +\infty[$
4) Établissons la relation $\ln(\alpha)=-1-\alpha.$
D'après la question 2), $\alpha$ est l'unique solution de l'équation $g(x)=0.$
Ce qui signifie que $g(\alpha)=0$
Par suite,
$\begin{array}{rcl} g(\alpha)=0&\Leftrightarrow&1+\alpha+\ln\alpha=0\\\\&\Leftrightarrow&\ln\alpha=-1-\alpha\end{array}$
D'où, la relation : $\boxed{\ln(\alpha)=-1-\alpha}$
II.
On considère la fonction $f$ définie par :
$$f(x)=\left\{\begin{array}{ccl} \dfrac{x\ln x}{1+x}&\text{si }& x>0 \\ \\ 0&\text{si }& x=0 \end{array}\right.$$
1) Montrons que $f$ est continue en $0$ puis sur $]0\;;\ +\infty[.$
Calculons $\lim\limits_{x\rightarrow 0^{+}}f(x)$
On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}f(x)&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{x\ln x}{1+x}\\\\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{0}{1}\\\\&=&0\end{array}$
Donc, $\lim\limits_{x\rightarrow 0^{+}}f(x)=f(0).$
D'où, $f$ est continue en $0.$
Par ailleurs, $\forall\;x_{0}\in\;]0\;;\ +\infty[\;;\ f$ est continue en $x_{0}.$
Par conséquent, $f$ est continue sur $]0\;;\ +\infty[$
2) Étudions la dérivabilité de $f$ en $0.$
Calculons $\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}$
On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{\dfrac{x\ln x}{1+x}}{x}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{x\ln x}{x(1+x)}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{\ln x}{1+x}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{-\infty}{1}\\ \\&=&-\infty\end{array}$
Donc, $\boxed{\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}=-\infty}$
Ainsi, la fonction $f$ n'est pas dérivable en $0.$
Interprétons graphiquement ce résultat.
Comme $\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}=-\infty$ alors, la courbe représentative de $f$ admet une demi-tangente verticale au point d'abscisse $0.$
3) Déterminons la limite de $f$ en $+\infty.$
On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}f(x)&=&\lim\limits_{x\rightarrow +\infty}\dfrac{x\ln x}{1+x}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{x}{x}\times\dfrac{\ln x}{\dfrac{1+x}{x}}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{\ln x}{\dfrac{1}{x}+1}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{+\infty}{0+1}\\ \\&=&+\infty\end{array}$
4) Montrons que, quel que soit $x$ élément de $]0\;;\ +\infty[$
$$f'(x)=\dfrac{g(x)}{(1+x)^{2}}$$
On a : $\forall\;x\in\;]0\;;\ +\infty[\;;\ f(x)=\dfrac{x\ln x}{1+x}$
Par suite,
$\begin{array}{rcl} f'(x)&=&\dfrac{(1+\ln x)(1+x)-x\ln x}{(1+x)^{2}}\\\\&=&\dfrac{1+x+\ln x+x\ln x-x\ln x}{(1+x)^{2}}\\\\&=&\dfrac{1+x+\ln x}{(1+x)^{2}}\\\\&=&\dfrac{g(x)}{(1+x)^{2}}\end{array}$
Ainsi, $\boxed{f'(x)=\dfrac{g(x)}{(1+x)^{2}}}$
En déduisons le signe de $f'(x)$ sur $]0\;;\ +\infty[.$
Comme $(1+x)^{2}>0$ alors, le signe de $f'(x)$ dépend uniquement du signe de $g(x).$
Or, $g(x)$ est négatif sur $]0\;;\ \alpha]$ et positif sur $[\alpha\;;\ +\infty[$
Par conséquent,
$\centerdot\ \ f'(x)\leq 0$ sur $]0\;;\ \alpha]$
$\centerdot\ \ f'(x)\geq 0$ sur $[\alpha\;;\ +\infty[$
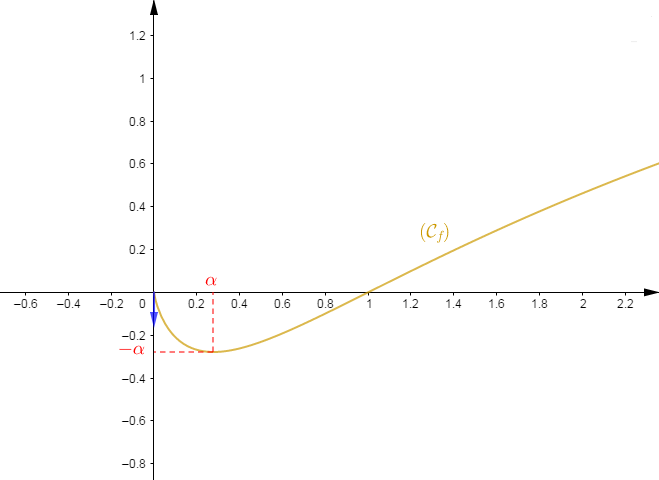
5) Montrons que $f(\alpha)=-\alpha.$
Soit : $f(\alpha)=\dfrac{\alpha\ln\alpha}{1+\alpha}$
Or, dans la première partie, à la question 4), on avait : $\ln\alpha=-1-\alpha.$
Donc, en remplaçant $\ln\alpha$ par son expression, on obtient :
$\begin{array}{rcl} f(\alpha)&=&\dfrac{\alpha\ln\alpha}{1+\alpha}\\\\&=&\dfrac{\alpha(-1-\alpha)}{1+\alpha}\\\\&=&\dfrac{-\alpha(1+\alpha)}{1+\alpha}\\\\&=&-\alpha\end{array}$
Ainsi, $\boxed{f(\alpha)=-\alpha}$
6) Dressons le tableau de variations de la fonction $f.$
$$\begin{array}{|c|lcccr|}\hline x&0&&\alpha&&+\infty\\ \hline f'(x)&|&-&0&+&\\ \hline&0&&&&+\infty\\f&&\searrow&&\nearrow&\\&&&-\alpha&&\\ \hline \end{array}$$
7) Représentons la courbe de $f$ dans le plan muni du repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$ Unité graphique : $5\;cm\;.$ Prendre $\alpha\approx 0.3.$

III.
1) A l'aide d'une intégration par parties, calculons l'intégrale
$$I=\int_{1}^{\mathrm{e}}x\ln(x) \mathrm{d}x$$
Posons : $u'=x\ $ et $\ v=\ln x$ alors, on a :
\begin{eqnarray} I&=&\int_{1}^{\mathrm{e}}x\ln(x) \mathrm{d}x\nonumber\\ \nonumber\\&=&\left[\dfrac{x^{2}\ln(x)}{2}\right]_{1}^{\mathrm{e}}-\int_{1}^{\mathrm{e}}\dfrac{x^{2}}{2x} \mathrm{d}x\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}}{2}-\int_{1}^{\mathrm{e}}\dfrac{x}{2} \mathrm{d}x\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}}{2}-\left[\dfrac{x^{2}}{4}\right]_{1}^{\mathrm{e}}\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}}{2}-\left(\dfrac{\mathrm{e}^{2}}{4}-\dfrac{1}{4}\right)\nonumber\\ \nonumber\\&=&\dfrac{2\mathrm{e}^{2}}{4}-\dfrac{\mathrm{e}^{2}}{4}+\dfrac{1}{4}\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}+1}{4}\nonumber \end{eqnarray}
D'où, $\boxed{I=\dfrac{\mathrm{e}^{2}+1}{4}}$
2) Montrons que pour tout $x$ élément de $[1\;;\ \mathrm{e}]$
$$\dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}$$
Soit $x\in[1\;;\ \mathrm{e}]$ alors, cela se traduit, sous forme d'intervalle par :
$$1\leq x\leq\mathrm{e}$$
Par suite,
$\begin{array}{rcl} 1\leq x\leq\mathrm{e}&\Rightarrow&1+1\leq 1+x\leq\mathrm{e}+1\\\\&\Rightarrow&\dfrac{1}{\mathrm{e}+1}\leq\dfrac{1}{1+x}\leq\dfrac{1}{2}\\\\&\Rightarrow&\dfrac{x\ln x}{\mathrm{e}+1}\leq\dfrac{x\ln x}{1+x}\leq\dfrac{x\ln x}{2}\end{array}$
D'où, $\boxed{\forall\;x\in[1\;;\ \mathrm{e}]\;;\ \dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}}$
En déduisons que :
$$\dfrac{\mathrm{e}^{2}+1}{4(\mathrm{e}+1)}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{\mathrm{e}^{2}+1}{8}$$
Comme $\dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}$ alors, par conservation de l'ordre de l'intégration, on obtient :
\begin{eqnarray}\dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}&\Rightarrow&\int_{1}^{\mathrm{e}}\dfrac{x\ln x}{\mathrm{e}+1}\mathrm{d}x\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\int_{1}^{\mathrm{e}}\dfrac{x\ln x}{2}\mathrm{d}x\nonumber\\ \nonumber\\ &\Rightarrow&\dfrac{1}{\mathrm{e}+1}\int_{1}^{\mathrm{e}}x\ln(x)\;\mathrm{d}x\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{1}{2}\int_{1}^{\mathrm{e}}x\ln(x)\;\mathrm{d}x\nonumber\\ \nonumber\\ &\Rightarrow&\dfrac{1}{\mathrm{e}+1}\times\dfrac{\mathrm{e}^{2}+1}{4}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{1}{2}\times\dfrac{\mathrm{e}^{2}+1}{4}\nonumber\\ \nonumber\\ &\Rightarrow&\dfrac{\mathrm{e}^{2}+1}{4(\mathrm{e}+1)}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{\mathrm{e}^{2}+1}{8}\nonumber \end{eqnarray}
D'où, $\boxed{\dfrac{\mathrm{e}^{2}+1}{4(\mathrm{e}+1)}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{\mathrm{e}^{2}+1}{8}}$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
mer, 01/11/2023 - 18:13
Permalien
Merci
Ajouter un commentaire