Corrigé Bac Maths S2 1er groupe 2015
Exercice 1 (3.5pts)
1) L'évènement contraire de "A sachant B" est ¯A sachant B.
2) Soient E et F deux évènements indépendants d'un même univers, on a : p(E∪F)=p(E)×p(¯F)+p(F)
3) Soit X une variable aléatoire qui suit une loi binomiale de paramètres n et p où n=4 et p∈]0, 1[. Si p(X=1)=8p(X=0) alors, p=23
4. Interprétations géométriques :
a) AM=1
b) AM=BM
c) OM′=AB
d) (→MB, →MA)=(→M′B, →M′A) [2π]
Exercice 2 (5pts)
1. Soit p(z)=z3+3z2−3z−5−20i, z∈C.
a) p(2+i)=(2+i)3+3(2+i)2−3(2+i)−5−20i=5−5+24i−24i=0:
D'où 2+i est une racine de p(z).
b) p(2+i)=0 donc p(z)=(z−2−i)q(z) avec q(z)=z2+(5+i)z+6+7i.
p(z)=0 si et seulement si z−2−i=0 ou z2+(5+i)z+6+7i=0.
On pose z2+(5+i)z+6+7i=0.
Δ=−18i
Les racines de Δ sont 3(1−i) et −3(1−i). D'où on a :
z1=−4+i et z2=−1−2i.
L'ensemble des solutions de l'équation p(z)=0 est :
S={2+i, −4+i, −1−2i}
2) Le plan complexe est rapporté au repère orthonormé (O; →u, →v)
Soient A(2+i), B(−1−2i) et C(−4+i).
a) Plaçons les points A, B et C.
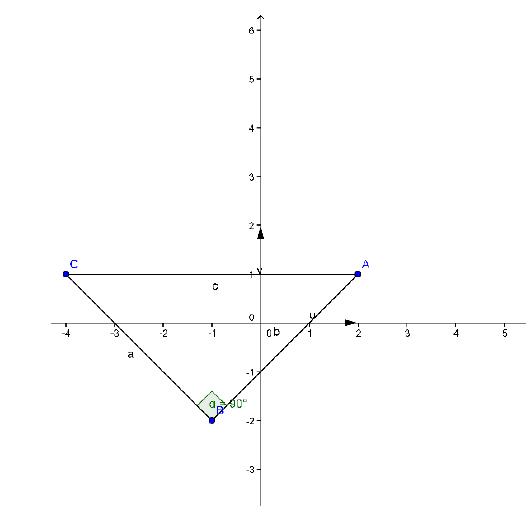
AB=3√2 et BC=3√2
b) On a
arg(zC−zBzA−zB)=arg(z→BCz→BA)=argz→BC−argz→BA=(→u, →BC)−(→u, →BA) [2π]==(→BA, →BC) [2π]
c) arg(zC−zBzA−zB)=arg(−1+i1+i)=arg(i)=π2 [2π].
d) D'après a) et b) ABC est un triangle rectangle isocèle en B.
3) a) r : M(z)↦M′(z′) telle que z′=az+b.
(1) {r(B)=Br(A)=C⇒(2) {azB+b=zBazA+b=zC
D'où a=zB−zCzB−zA=−1+i1+i=i et b=zB(1−a)=(−1−2i)(1−i)=−3−i.
Donc l'application f associée à r est définie par f(z)=iz−3−i
b) Les éléments caractéristiques de r sont :
– Le centre B d'affixe −1−2i.
– L'angle θ=π2
4. T : M(z)↦M′(z′) telle que z′=iα2z+α, α∈C.
a) Si T est une homothétie de rapport 2 alors iα2=2.
iα2=2 ⇔ α2=−2i ⇔ α2=(1−i)2.
D'où : α=1−i ou α=−1+i
b) Si |α|=√2 et argα=−π4 alors α=1−i. D'où z′=2z+1−i
Donc T est une homothétie de centre Ω d'affixe −1+i et de rapport k=2.
5) g=r∘T avec α=1−i.
a) Soit t l'application de C dans C associée à T. On a :
h(z)=f∘t(z)=f(2z+1−i)=i(2z+1−i)−3−i
d'où h(z)=2iz−2
b) g est une similitude directe de :
– centre Ω0 d'affixe −25−45i,
– rapport k=2,
– angle θ=π2.
g=S(Ω0(−25−45i), 2, π2)
Exercice 3 (2.5pts)
1) Le coefficient de corrélation linéaire r est défini par r=Cov(X, Y)σXσY.
D'où : r≈0.69.
2) a) La droite de régression de Y en X, (DY/X), a pour équation y=92.59x−4.35.
b) Il faut investir 3.29 milliards de FCFA si l'on désire un chiffre d'affaire de 300 milliards.
Exercice 4 (9pts)
A) 1) Soit I(α)=∫α0et(t+2)dt.
En intégrant par parties I(α)=∫α0et(t+2)dt, on obtient : I(α)=eα(α+1)−1.
D'où : I(x)=ex(x+1)−1.
2) k étant une fonction dérivable sur R, soit h telle que h(x)=k(x)e−x, ∀x∈R
a) Si h vérifie la condition h′(x)+h(x)=x+2 alors on a : k′(x)e−x−k(x)e−x+k(x)e−x=x+2, d'où k′(x)=(x+2)ex
b) Déduisons-en h. Puisque k′(x)=(x+2)ex.
D'après 1) I est une primitive de k′ , donc k(x)=ex(x+1)−1+c, avec c une constante.
Or, h(0)=2 nous donne k(0)=2 donc c=2. Ainsi k(x)=ex(x+1)+1
D'où : h(x)=x+1+e−x
B) I) 1) Étude les variations de la fonction g, définie par g(x)=x+1+e−x, sur R.
Domaine de définition de g :
g étant définie partout dans R, d'où Dg=R.
Continuité et dérivabilité :
– La fonction x↦ x+1 est une fonction polynôme, elle est continue et dérivable sur R
– La fonction x↦ −x est continue et dérivable sur R, de même que la fonction x↦ ex. Par composée, la fonction x↦ e−x est continue et dérivable sur R,
– Par somme g est continue et dérivable sur R.
Calcul de g′(x)
g′(x)=ex−1ex
D'où : g′(x)≥0 pour tout x≥0 et g′(x)<0 pour tout x<0.
Tableau de variations de g :
limx→−∞g(x)=limx→−∞x(1+1x−e−x−x)=+∞
limx→+∞g(x)=limx→+∞x+1+e−x=+∞
x−∞0+∞g′(x)−0++∞+∞g↘↗2
2) ∀x∈R, g(x)≥2 d'après le tableau de variations de g, ce qui implique g est strictement positif.
II) f(x)=ln(x+1+e−x).
1) Les variations de la fonction f :
– Df=R.
– limx→−∞f(x)=+∞, limx→+∞f(x)=+∞
– f est continue et dérivable sur R par composée.
– Dérivée :
f′(x)=1−e−xx+1+e−x
– Sens de variations de f :
f′(x) a le même signe que 1−e−x.
f′(x)≥0 si x≥0,
f′(x)<0 si x<0.
– Tableau de variations de f :
x−∞0+∞f′(x)−0++∞+∞f↘↗ln2
2) M(xlnx), N(xln(x+1+e−x))
a) ¯MN=ln(x+1+e−x)−lnx.
D'une part, la fonction ln étant croissante et x+1+e−x>x, d'où ln(x+1+e−x)>lnx, donc ¯MN>0(1)
D'autre part, ¯MN=ln(dfracx+1+e−xx).
Or si x>0 alors e−x<1, d'où x+1+e−x<x+2, ainsi ln(dfracx+1+e−xx)<ln(dfracx+2x), donc ¯MN<ln(x+2x)(2)
(1) et (2) donnent : 0<¯MN<ln(x+2x).
b) limx→+∞ln(x+2x)=0
donc 0<limx→+∞¯MN<0 d'où d'après le théorème des gendarmes limx→+∞¯MN=0
3) a) Démontrons que f(x)=−x+ln(xex+ex+1), ∀x∈R.
On sait que f(x)=ln(x+1+e−x)=ln((x+1)ex+1ex).
Cherchons le signe de m(x)=(x+1)ex+1.
On a m′(x)=(x+2)ex, et elle s'annule en -2.
m étant décroissante sur ]−∞; −2] et croissante sur [−2; +∞[ alors m admet un minimum en -2 et m(−2)=e2−1e2.
Donc, pour tout x, m(x)>0. Ainsi donc f(x)=−x+ln(xex+ex+1)
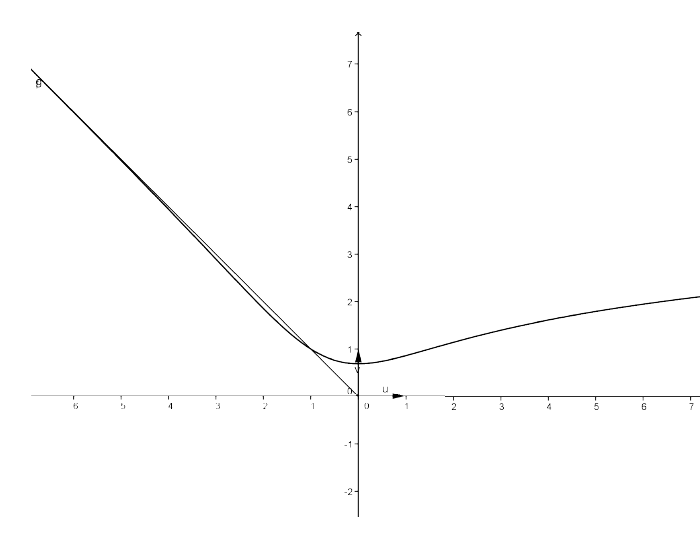
b) D'après a) f(x)=−x+ln(xex+ex+1). Or limx→−∞[f(x)+x]=limx→−∞ln(xex+ex+1)=0. Donc (Cf) admet une asymptote oblique (Δ), d'équation y=−x au voisinage de −∞.
Position de (Cf) par rapport à (Δ) :
Cherchons le signe de ln((x+1)ex+1).
ln((x+1)ex+1)≥0 si (x+1)≥0.
Alors, (Cf) est en dessous de (Δ) au voisinage de −∞.
Au voisinage de +∞, limx→+∞f(x)x=limx→+∞ln(x+1)x=0.
Donc, (Cf) admet une branche infinie de direction l'axe (Ox).

Commentaires
Anonyme (non vérifié)
lun, 07/03/2023 - 18:23
Permalien
Merci
Ajouter un commentaire