Bac Maths D, Benin 2017

Un système d'éclairage peu ordinaire.

Tafè est un sculpteur passionné des mathématiques. Il a conçu, pour éclairer son salon, un lampadaire représenté par le solide $(S)$ suivant :

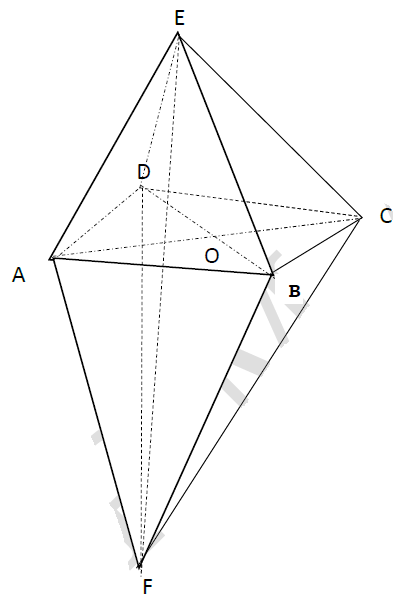
Le solide $(S)$ est tel que :

$\bullet\ $Le quadrilatère $ABCD$ est un carré de centre $O.$

$\bullet\ $La droite $(EF)$ est perpendiculaire au plan $(ABS)$ en $O.$

$OA=OB=OE=1$ et $OF=2OE$, l'unité de longueur étant $2\,dm.$

$\bullet\ $La face $FBC$ a été décorée avec des configurations planes.

$\bullet\ $Deux ampoules ont été placées en des endroits qui sont assimilés aux points $H$ et $K$ projetés orthogonaux de $A$ respectivement sur le plan $(FBC)$ et sur $(ED).$ Vidaho, fils de Tafè, a été toujours émerveillé par le lampadaire. À présent qu'il est en classe terminale scientifique, il veut utiliser ses connaissances pour étudier certaines informations reçues de son père et qui ont servi à sa conception. Afin de connaître certaines caractéristiques du lampadaire, Vidaho a supposé que l'espace est muni du repère orthonormé direct $(O\;,\ \overrightarrow{OA}\;\ \overrightarrow{OB}\;,\ \overrightarrow{OE}).$

Tu es invité(e) à trouver des réponses aux préoccupations de Vidaho en résolvant les trois problèmes ci-après.

1. Détermine dans le repère $(O\;,\ \overrightarrow{OA}\;\ \overrightarrow{OB}\;,\ \overrightarrow{OE}).$ les coordonnées des points $C$, $D$ et $F.$

2. a) Démontre que le plan $(FCB)$ a pour équation cartésienne $2x−2y+z+2=0.$

b) Détermine une représentation paramétrique de la droite passant par $A$ et perpendiculaire au plan $(FCD).$

c) Détermine les coordonnées du point $H.$

3. a) Détermine une équation du plan $(\mathcal{P})$ passant par $A$ et perpendiculaire à la droite $(DE).$

b) Détermine les coordonnées du point $K.$

c) Calcule la distance $KH.$

4. Calcule le volume du solide $(\mathcal{S}).$

La configuration représentée dans le plan $(FBC)$ a été obtenue à partir de la courbe représentative $\left(\mathcal{C_{f}}\right)$ dans un repère orthonormé, de la fonction $f$ de $\mathbb{R}$ vers $\mathbb{R}$ définie par :
$$\left\lbrace\begin{array}{lcl} f(x)&=&\dfrac{1}{x-\ln x}+\dfrac{\ln x}{x}\;,\ x\neq 0\\\\ f(0)&=&0 \end{array}\right\rbrace$$

On considère la fonction $g$ définie sur $]0\ ;\ +\infty[$ par : $g(x)=x−\ln x.$

5. a) Étudie le sens de variation de $g.$

b) Déduis-en que pour tout $x$ élément de $]0\ ;\ +\infty[$, on a $g(x)\geq 1.$

6. Soit $\mathcal{D_{f}}$ l'ensemble de définition de $f.$

a) En utilisant la question 5. b)

démontre que $\mathcal{D_{f}}=[0\ ;\ 1[\cup]1\ ;\ +\infty[.$

b) Justifie que $f$ est continue sur chacun des intervalles $[0\ ;\ 1[$ et $]1\ ;\ +\infty[.$

c) Étudie la dérivabilité de $f$ à droite en $0$ et donne une interprétation géométrique du résultat.

d) Détermine les limites de $f$ aux bornes de $\mathcal{D_{f}}.$
 
7. Sur le dessin ci-après, on a représenté la courbe $(\Gamma)$ de la fonction dérivée $f'$ de $f$, et son asymptote d'équation $x=1.$

À partir de la courbe $(\Gamma).$

a) Justifie que l'équation $f'(x)=0$ admet dans $]0\ ;\ 1[\cup]1\ ;\ +\infty[$ deux solutions $\alpha$ et $\beta$ avec $\alpha<\beta.$

b) Détermine le signe de $f'(x)$ pour $x$ élément de $]0\ ;\ 1[\cup]1\ ;\ +\infty[.$

8. Détermine le sens de variation de $f$ puis dresse son tableau de variation.

9. Étudie les branches infinies de la courbe $\left(\mathcal{C_{f}}\right)$ puis trace $\left(\mathcal{C_{f}}\right).$

L'installation électrique à l'intérieur du lampadaire est configurée pour qu'au déclenchement de l'interrupteur pour l'allumer, les deux ampoules $A_{1}$ et $A_{2}$ qui s'y trouvent puissent être allumées ou éteintes, et cela indépendamment l'une de l'autre.

Après de nombreuses observations, Vidaho a pu établir que la probabilité pour que l'ampoule $A_{1}$ s'allume est $0.8$ alors que la probabilité pour que l'ampoule $A_{2}$ s'allume est $0.6.$

10. Détermine la probabilité pour qu'à un déclenchement donné de l'interrupteur pour allumer le lampadaire :

a) une et une seule des deux ampoules soit allumée ;

b) les deux ampoules soient simultanément allumées.

11. Pendant le réveillon de la saint-Sylvestre, l'interrupteur a été déclenché $n$ fois pour allumer le lampadaire, $n$ étant un entier naturel supérieur à $1.$

a) Détermine la probabilité $p_{n}$ pour qu'à chaque fois les ampoules soient allumées.

b) Détermine le plus petit entier naturel $n$ tel que $p_{n}<0.01.$