Bac Maths D, Maroc 2016
Exercice 1
$U_{0}=2$ et $U_{n+1}=\dfrac{1}{16}U_{n}+\dfrac{15}{16}$ pour tout entier naturel $n\in\mathbb{N}$
1. a) Montrer par récurrence que $U_{n}>1$ pour tout entier naturel $n\in\mathbb{N}$
b) Vérifier que ∶ $U_{n+1}-U_{n}=−\dfrac{15}{16}\left(U_{n}-1\right)$ puis montrer que la suite $\left(U_{n}\right)$ est décroissante.
c) En déduire que la suite $\left(U_{n}\right)$ est convergente.
2. Soit $\left(V_{n}\right)$ la suite numérique telle que $V_{n}=U_{n}-1$ pour tout entier naturel $n\in\mathbb{N}.$
a) Montrer que $\left(V_{n}\right)$ est une suite géométrique de raison $\dfrac{1}{16}$ et exprimer $V_{n}$ en fonction de $n.$
b) Montrer que $U_{n}=1+\left(\dfrac{1}{16}\right)^{n}$ pour $n\in\mathbb{N}$ , puis déterminer la limite de la suite $\left(U_{n}\right)$
Exercice 2
1. a) Montrer que $\overrightarrow{OA}\wedge\overrightarrow{OB}=2\vec{i}-2\vec{j}+\vec{k}$
b) Montrer que $2x+2y+z=0$ est une équation cartésienne du plan $(OAB).$
2. Soit $(\mathcal{S})$ la sphère d'équation $x^{2}+y^{2}+z^{2}-6x-6y-6z=0.$
Montrer que le centre de la sphère $(\mathcal{S})$ est le point $\Omega(3\;,\ -3\;,\ 3)$ et son rayon est $5.$
3. a) Montrer que le plan $(OAB)$ est tangent à la sphère $(\mathcal{S}).$
b) Déterminer les coordonnées de $H$ point de contact du plan $(OAB)$ et la sphère $(\mathcal{S}).$
Exercice 3
2. On considère, dans le plan complexe rapporté à un repère orthonormé direct $(O\;,\ \vec{u}\;,\ \vec{v})$, les points $A$, $B$, $C$ et $\Omega$ d'affixes respectives $a$, $b$, $c$ et $\omega$ tel que : $a=4+5\mathrm{i}$, $b=3+4\mathrm{i}$ et $c=6+7\mathrm{i}$ et $\omega=4+7\mathrm{i}$
a) Calculer $\dfrac{c-b}{a-b}$ et en déduire que les points $A$, $B$ et $C$ sont alignés.
b) Soit $z$ l'affixe d'un point $M$ du plan et $z'$ l'affixe du point $M'$ image de $M$ par la rotation $R$ de centre $\Omega$ et d'angle $-\dfrac{\pi}{2}.$
Montrer que ∶ $z'=-\mathrm{i}z-3+11\mathrm{i}$
c) Déterminer l'image du point $C$ par la rotation $R$ puis donner une forme trigonométrique du nombre : $\dfrac{a-\omega}{c-\omega}$
Exercice 4
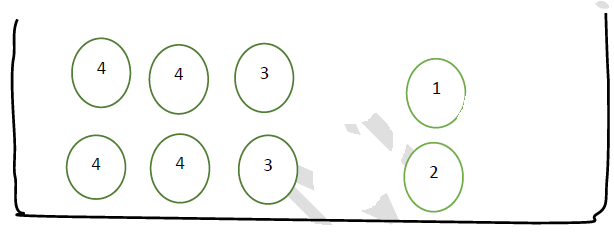
On considère l'épreuve suivante : On tire au hasard successivement et sans remise deux boules de l'urne.
1. Soit l'évènement $A$ : les deux boules tirées portent deux nombres pairs.
Montrer que $p(A)=\dfrac{1}{3}$
2. On répète l'épreuve précédente trois fois en remettant à chaque fois les deux boules tirées dans l'urne.
Soit $X$ la variable aléatoire qui est égale au nombre de fois où l'évènement $A$ est réalisé.
Montrer que $p(X=1)=\dfrac{4}{9}$ puis démontrer la loi de probabilité de la variation aléatoire $X$
Problème :
Le tableau ci-dessous est le tableau de variation de la fonction $g$ sur l'intervalle $]0\ ;\ +\infty[$
1. Calculer $g(1)$
2. Déduire à partir du tableau de variation que : $g(x)>0$ pour tout $x$ $]0\ ;\ +\infty[$
$$\begin{array}{|c|lcccr|} \hline x&0& &1& &+\infty\\ \hline g'(x)& &-&0&+&\\ \hline g(x)&+\infty&\searrow& &\nearrow&+\infty\\ & & &g(1)& &\\ \hline \end{array}$$
II. On considère la fonction numérique $f$ définie sur $]0\ ;\ +\infty[$ par : $$f(x)=3-3x+2(x+1)\ln x$$
Soit $(\mathcal{C})$ la courbe représentative de la fonction $f$ dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$ $($unité : $2\,cm).$
1. Montrer que $\lim\limits_{x\rightarrow 0^{-}}f(x)=-\infty$ et donner une interprétation géométrique à ce résultat
2. a) Montrer que $\lim\limits_{x\rightarrow +\infty}f(x)=+\infty.$
$($pour calculer cette limite on pourra d'écrire $f(x)$ sous forme ∶ $)$ $$f(x)=x\left[\dfrac{3}{x}-3+2\left(1+\dfrac{1}{x}\right)\ln x\right]$$
b) Montrer que la courbe $(\mathcal{C})$ admet une branche parabolique de direction l'axe des ordonnées au voisinage de $+\infty$
3. a) Montrer que $f′(x)=g(x)$ pour tout $x$ de $]0\ ;\ +\infty[$
b) En déduire que la fonction $f$ est strictement croissante sur $]0\ ;\ +\infty[$ et dresser le tableau de variation de la fonction $f$ sur $]0\ ;\ +\infty[$
4. a) Montrer que $I(1\;,\ 0)$ est un point d'inflexion de la courbe $(\mathcal{C}).$
b) Montrer que $y=x-1$ est une équation cartésienne de la droite $(T)$ tangente à la courbe $(\mathcal{C})$ au point $I.$
c) Tracer dans le même repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$, la droite $(T)$ et la courbe $(\mathcal{C}).$
5. a) Montrer que $$\int^{2}_{1}\left(1+\dfrac{x}{2}\right)\mathrm{d}x\dfrac{7}{4}$$
b) En utilisant une intégration par parties, montrer que :$$\int_{1}^{2}(x+1)\ln x\mathrm{d}x=4\ln 2-\dfrac{7}{4}$$
6. Résoudre graphiquement l'inéquation : $(x+1)\ln x\geq\dfrac{3}{2}(x-1)$ pour $x$

Ajouter un commentaire