Bac Maths D, Maroc 2017

L'espace est muni d'un repère orthonormé direct $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}).$

On considère la sphère $(S)$ d'équation : $x^{2}+y^{2}-2x-2y-1=0$ et le plan $(\mathcal{P})$ d'équation ∶ $y-z=0.$

1. a) Montrer que le centre de la sphère $(S)$ est le point $\Omega(1\ ;\ 1\ ;\ 1)$ et son rayon est $2.$

b) Calculer $d(\Omega\;,\ \mathcal{P})$ et en déduire que le plan $(\mathcal{P})$ coupe la sphère $(S)$ suivant un cercle $(\mathcal{C})$

c) Déterminer le centre et le rayon de $(\mathcal{C}).$

2. Soit $(\Delta)$ la droite passant par le point $A(1\;,\ -2\;,\ 2)$ et orthogonale au plan $(\mathcal{P}).$

a) Montrer que $\vec{u}(0\;,\ 1\;,\ -1)$ est un vecteur directeur de la droite $(\Delta).$

b) Montrer que $||\overrightarrow{\Omega A}\wedge\vec{u}||=\sqrt{2}||\vec{u}||$ et en déduire que la droite $(\Delta)$ coupe la sphère $(S)$ en deux points.

c) Déterminer les coordonnées de chacun des deux points de contact de la droite $(\Delta)$ et la sphère $(S).$

Une urne contient huit boules indiscernables au toucher : cinq boules blanches, trois boules rouges et deux boules vertes (voir figure ci-dessous)

 
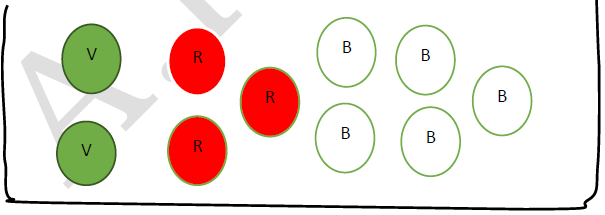
On tire au hasard et simultanément quatre boules de l'urne.

1. Soit $A$ l'évènement Parmi les quatre boules tirées, il y'a une seule boule verte seulement et $B$ l'évènement Parmi les quatre boules tirées, il y'a exactement trois boules de même couleur.

Montrons que $p(A)=\dfrac{8}{15}$ et $p(B)=\dfrac{19}{70}$
                                                                                       
2. Soit $X$ la variable aléatoire qui à chaque tirage associe le nombre de boules vertes tirées.

a) Montrer que $p(X=2)=\dfrac{2}{15}$
                                                                                                  
b) Déterminer la loi de probabilité de la variable aléatoire $X$ et montrer que l'espérance mathématique est égale à $\dfrac{4}{5}.$

1. Résoudre dans l'ensemble des nombres complexes $\mathbb{C}$ l'équation : $z^{2}+4z+8=0$

2. On considère, dans le plan complexe rapporté à un repère orthonormé direct $(O\;,\ \vec{u}\;,\ \vec{v})$, les points $A$, $B$ et $C$ d'affixes respectives $a$, $b$ et $c$ tel que : $a=-2+2\mathrm{i}$, $b=4-4\mathrm{i}$ et $c=4+8\mathrm{i}$

a) Soit $z$ l'affixe d'un point $M$ du plan et $z'$ l'affixe du point $M'$ image de $M$ par la rotation $R$ de centre $A$ et d'angle $\dfrac{\pi}{2}.$

Montrer que ∶ $z'=-\mathrm{i}z-4$

b) Vérifier que le point $B$ est l'image du point $C$ par la rotation $R$ et en déduire la nature du triangle $ABC.$

3. Soit $\omega$ l'affixe du point $\Omega[BC].$

a) Montrer que $|c-\omega|=6$

b) Montrer que l'ensemble des points $m$ d'affixe $z$ tel que $|z-\omega|=6$ est le cercle circonscrit au triangle $ABC.$

On considère la suite numérique $\left(U_{n}\right)$ définie par :
 
$U_{0}=17$ et $U_{n+1}=\dfrac{1}{4}U_{n}+12$ pour tout entier naturel $n$                                      

1. a) montrer par récurrence que : $U_{n}>16$ pour tout entier naturel $n$                                       

b) Montrer que la suite $\left(U_{n}\right)$ est décroissante et en déduire qu'elle est convergente.

2. Soit $\left(V_{n}\right)$ la suite numérique tel que : $V_{n}=U_{n}-16$ pour tout entier naturel $n.$

a) montrer que $\left(V_{n}\right)$ est une suite géométrique.
 
b) Montrer que $U_{n}=16+\left(\dfrac{1}{4}\right)^{n}$ pour tout entier naturel $n$ puis déterminer la limite de la suite $\left(U_{n}\right)$

c) Déterminer la plus petite valeur de l'entier naturel n pour laquelle $U_{n}<16.001.$

I. Soit $g$ la fonction numérique définie sur $\mathbb{R}$ par ∶ $g(x)=1-(x+1)^{2}\mathrm{e}^{x}$

1. Vérifier que ∶ $g(0)=0$

2. A partir de la représentation graphique de la fonction $g$ (voir figure ci-dessous).

Montrer que : $g(x)\geq 0$ pour tout $x\in]−\infty\;,\ 0]$ et que $g(x)\leq 0$ pour tout $x\in[0\;,\ +\infty[$

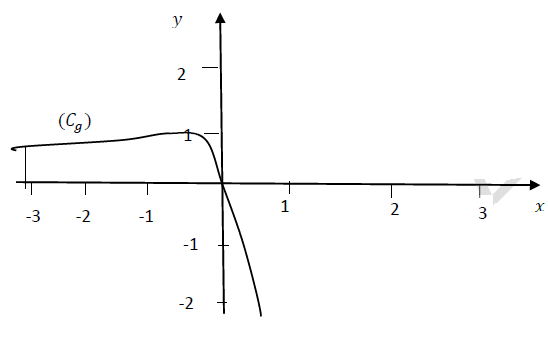
II. On considère la fonction numérique $f$ définie sur $\mathbb{R}$ par : $$f(x)=x+1-(x^{2}+1)\mathrm{e}^{x}$$

Soit $\mathcal{C_{f}}$ la courbe représentative de la fonction $f$ dans un repère orthonormé $(O\;,\ \vec{i}\ \vec{j})$ $($unité : $2\,cm).$

1. a) Vérifier que ∶ $f(x)=x+1-4\left(\dfrac{x}{2}\mathrm{e}^{\dfrac{x}{2}}\right)^{2}-\mathrm{e}^{x}$ pour tout réel $x$ puis en déduire que $\lim\limits_{x\rightarrow -\infty}f(x)=-\infty$
 
Calculer $\lim\limits_{x\rightarrow -\infty}[f(x)-(x+1)]$ et en déduire que la droite $(\mathcal{D})$ d'équation $y=x+1$ est une asymptote à la courbe $\left(\mathcal{C_{f}}\right)$ au voisinage de $−\infty.$

c) Montrer que la courbe $\left(\mathcal{C_{f}}\right)$ est au-dessous de la droite $(\mathcal{D}).$

2. a) Montrer que $\lim\limits_{x\rightarrow +\infty}f(x)=-\infty$

$($On pourra écrire $f(x)$ sous la forme $x\left[1+\dfrac{1}{x}-\left(x+\dfrac{1}{x}\right)\mathrm{e}^{x}\right])$

b) Montrer que la courbe $\left(\mathcal{C_{f}}\right)$ admet au voisinage de $+\infty$ une branche parabolique dont on précisera la direction.

3. a) Montrer que $f'(x)=g(x)$ pour tout réel $x.$

b) Montrer que la fonction $f$ est croissante sur l'intervalle $]−\infty\;,\ 0]$ et décroissante sur l'intervalle $[0\;,\ +\infty[$ et dresser le tableau de variations de la fonction $f$ sur $\mathbb{R}$

c) Montrer que la courbe $\left(\mathcal{C_{f}}\right)$ possède deux points d'inflexion d'abscisses $-3$ et $-1.$

4. Construire, dans le même repère orthonormé $(O\;,\ \vec{i}\ \vec{j})$, la droite $(\mathcal{D})$ et la courbe $\left(\mathcal{C_{f}}\right).$

$($on prendra $f(−3)\approx −2.5$ et $f(−1)\approx −0.7)$  

5. a) Vérifier que la fonction $H\ :\ x\longmapsto(x-1)\mathrm{e}^{x}$ est une fonction primitive de la fonction $h\ :\ x\longmapsto x\mathrm{e}^{x}$ sur $\mathbb{R}$ puis montrer que :
$$\int^{-1}_{0}x\mathrm{e}^{x}\mathrm{d}x=\dfrac{2}{\mathrm{e}}-1$$

b) Montrer à l'aide d'une intégration par parties, que :
$$\int^{-1}_{0}(x^{2}+1)\mathrm{e}^{x}\mathrm{d}x=3\left(1-\dfrac{2}{\mathrm{e}}\right)$$

c) Calculer, en $cm^{2}$, l'aire du domaine plan limité par la courbe $\left(\mathcal{C_{f}}\right)$, la droite $(\mathcal{D})$, l'axe des abscisses et la droite d'équation $x=-1.$