Bac Maths D, Tunisie 2015

L'espace est rapporté à un repère orthonormé direct $(O_;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}).$

On considère les points $A(1\;,\ 1\;,\ 0)$, $B(1\;,\ -1\;,\ 2)$, $C(0\;,\ 1\;,\ 1)$ et $D(1\;,\ 1\;,\ 4).$

1. a) Montrer que $A$, $B$ et $C$ déterminent un plan qu'on notera $(\mathcal{P}).$

b) Justifier que $(\mathcal{P})$ est d'équation  $x+y+z-2=0.$

c) Vérifier que $D$ n'appartient pas au plan $(\mathcal{P}).$

2. Soit $\mathcal{G}$ le cercle circonscrit au triangle $ABC$ et $H$ le milieu du segment $⦋AB⦌.$

a) Montrer que le triangle $ABC$ est rectangle en $C$ ?

b) En déduire que $H$ est le centre du cercle $\mathcal{G}.$

c) Soit $\Delta$ la droite perpendiculaire au plan $(\mathcal{P})$ passant par le point $H.$
 
Justifier qu'une représentation paramétrique de $\Delta$ est :
$$\left\lbrace\begin{array}{lcl} x&=&1+\alpha\\ y&=&\alpha\quad;\quad\alpha\in\mathbb{R}\\  z&=&1+\alpha \end{array}\right\rbrace$$
 
4. Soit $M$ un point de $\Delta.$

a) Justifier que $MA=MB=MC.$

b) Montrer qu'il existe un unique point $I$ de $\Delta$ tel que $IA=ID.$

Donner ses coordonnées.

c) Déduire de ce qui précède, que les points $A$, $B$, $C$ et $D$ appartiennent à une même sphère $(\mathcal{S})$ dont on précisera le centre et le rayon.

Dans l'annexe ci-jointe (Figure 1), $(O\;,\ \vec{u}\;,\ \vec{v})$ est un repère orthonormé direct du plan et $(\mathcal{C})$ est le cercle de centre $O$ et de rayon $\sqrt{3}.$

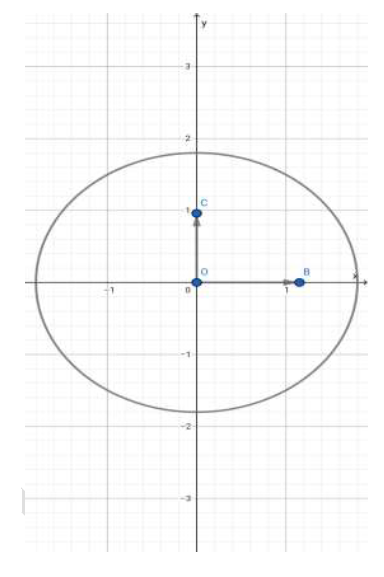
1. Soit $A$ l'affixe $a=1+\mathrm{i}\sqrt{2}$

a) Montrer que $A$ appartient à $(\mathcal{C}).$

b) Placer $A.$

2. On considère dans $\mathcal{C}$, l'équation $(E)\ :\ z^{2}-2\mathrm{i}\sqrt{3}z-6\mathrm{i}\sqrt{2}=0.$

a) Montrer que le discriminant $\Delta$ de l'équation $(E)$ est égale à $12a^{2}.$

b) En déduire que les solutions de l'équation $(E)$ sont :

$z_{1}=\sqrt{3}[−1+\mathrm{i}(1-\sqrt{2})]$  et  $z_{2}=\sqrt{3}[1+\mathrm{i}(1+\sqrt{2})]$   

3. On considère le point $K$ d'affixe $z_{k}=\mathrm{i}\sqrt{3}$ et on désigne par $M_{1}$ et $M_{2}$ les points d'affixes respectives $z_{1}$ et $z_{2}.$

a) Vérifier que $K$ est le milieu du segment $\left[M_{1}M_{2}\right].$

b) Montrer que $\dfrac{z_{2}-z_{1}}{a}=2\sqrt{3}.$

En déduire que la droite $\left[M_{1}M_{2}\right]$ est parallèle à la droite $(OA).$

c) Montrer que $M_{1}M_{2}=6.$

d) Placer le point $K$ et construire alors les points $M_{1}M_{2}.$

On appelle capacité vitale chez l'homme, le volume d'aire maximum pouvant être mobilisé par une aspiration forcée suivie d'une expiration forcée.

Le tableau ci-dessous sonne la capacité vitale $C$, exprimée en $cm^{3}$, chez les hommes âgés de $40$ ans en fonction de leur taille $t$ exprimée en $cm.$
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|} \hline t\text{ (en cm)}&152&156&160&166&170&174&178&180&182\\ \hline C\text{ (en }cm^{3})&3525&3620&3710&3850&3945&1035&4130&4175&4220\\ \hline \end{array}$$

1. a) Donner une valeur approchée à $10^{-5}$ près du coefficient de corrélation linéaire entre $t$ et $C.$

b) Justifier que l'on peut procéder à un ajustement affine par la méthode des moindres carrés de la série $(t\ ;\ C).$

c) Donner une équation de la droite de régression de $C$ en $t.$

$($Les coefficients seront arrondis à $10^{-2}$ près$).$

d) Déduire de cet ajustement une estimation de la capacité vitale d'un homme âgé de $40$ ans et de taille égale à $188\,cm$ ?

2. En fait, la capacité vitale $C$ $($exprimée en $cm^{3})$ chez l'homme dépend de sa taille $t$ $($exprimée en $cm)$ et de son âge $g$ (exprimé en année).

De nombreuses expériences ont permis d'exprimer $C$ en fonction de $t$ et $g$ selon la relation $C=\alpha t+\beta g+754$, où $\alpha$ et $\beta$ sont des constantes $($ne dépendant pas de $t$ et $g).$

a) Donner l'expression $C$ pour $g=40.$

b) En déduire, en utilisant $1.c$, les valeurs de $\alpha$ et $\beta.$

3. Estimer la capacité vital d'un homme âgé de $50$ ans et mesurant $188\,cm.$

Soit la fonction définie sur $I=]0\ ;\ +\infty[$ par $f(x)=x-\dfrac{\ln x}{x}$

On désigne par $\mathcal{G}$ la courbe représentative de $f$ dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}).$
 
1. a) Calculer $\lim\limits_{x\to 0^{+}}f(x)$, $\lim\limits_{x\to +\infty}f(x)$, et $\lim\limits_{x\to +\infty}f(x)-x.$

b) En déduire que la courbe $\mathcal{G}$ admet deux asymptotes que l'on précisera.

c) Étudier la position de $\mathcal{G}$ par rapport à la droite $\Delta$ d'équation $y=x.$
 
2. a) Montrer que, pour tout réel $x$ de $I$, $f'(x)=\dfrac{(x^{2}−1)+\ln x}{x^{2}}.$   
 
b) Montrer que $(x^{2}-1)$ et $\ln x$ sont de même signe sur chacun des intervalles $J=]0\;,\ 1[$ et $K=]1\,\ +\infty[.$     
 
c) En déduire le signe de $f'(x)$ sur chacun des intervalles $J$ et $K.$     
 
d) Montrer que $1$ est l'inique solution de l'équation $f'(x)=0.$     
 
e) Dresser le tableau de variation de $f.$
 
3. a) Montrer que la courbe $\mathcal{G}$ admet une unique tangente $D$ parallèle à la droite $\alpha.$           
 
Préciser les coordonnées du point $B$, point de contact de $\mathcal{G}$ et $\mathcal{D}.$
 
b) Donner une équation de $\mathcal{D}.$
 
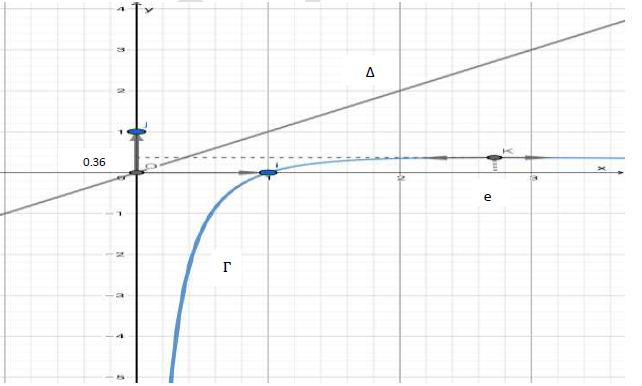
4. Dans l'annexe ci-jointe (Figure 2), on a tracé relativement au repère $(O\;,\ \vec{i}\;,\ \vec{j})$ la droite $\Delta$ et la courbe $(\Gamma)$ d'équation $y=\dfrac{\ln x}{x}.$       
 
a) Soit le point $A\left(\dfrac{1}{\mathrm{e}}\ ;\ 0\right)$            
 
Placer le point $A$ et vérifier que $A$ appartient à $\mathcal{D}.$        
 
b) Tracer la droite $\mathcal{D}$ et placer $B.$        

c) Tracer la courbe $\mathcal{G}.$

5. Soit $A$ l'aire de la partie du plan limité par la courbe $\mathcal{G}$, la droite $\alpha$ et les droites d'équations $x=\dfrac{1}{\mathrm{e}}$ et $x=\mathrm{e}.$

Calculer  $A.$