Bac Maths, ES/L Antilles-Guyane 18 juin 2019
Exercice 1 (5 points)
Commun à tous les candidats
La partie C est indépendante des parties A et B.
Une grande enseigne décide d'organiser un jeu permettant de gagner un bon d'achat.
Le jeu se déroule en deux étapes :
$\bullet\ $Étape 1 :
Chaque client tire au hasard une carte sur laquelle figure un nombre de $1$ à $50$, chaque numéro ayant la même probabilité d'être découvert ;
$\bullet\ $Étape 2 :
$-\ $ s'il découvre un numéro compris entre $1$ et $15$, il fait tourner une roue divisée en $10$ secteurs de même taille dont $8$ secteurs contiennent une étoile ;
$-\ $ sinon, il fait tourner une autre roue divisée elle aussi en $10$ secteurs de même taille dont un seul secteur contient une étoile.
Un bon d'achat est gagné par le client si la roue s'arrête sur une étoile.
Partie A
Un client joue à ce jeu.
On note :
$N$ l'évènement « Le client découvre un numéro entre $1$ et $15$ » ;
$E$ l'évènement « Le client obtient une étoile ».
1. a. Justifier que $P(N)=0.3$ et que $P_{N}(E)=0.8.$
b. Représenter cette situation à l'aide d'un arbre pondéré.
2. Calculer la probabilité que le client trouve un numéro entre $1$ et $15$ et une étoile.
3. Justifier que la probabilité que le client gagne un bon d'achat est égale à $0.31.$
4. Le client a gagné un bon d'achat.
Quelle est la probabilité qu'il ait obtenu un numéro entre $1$ et $15$ à la première étape ?
Partie B
Le montant d'un bon d'achat est de $10$ euros.
Pour ce jeu, le directeur de l'hypermarché a prévu un budget de $250$ euros par tranche de $100$ clients y participant.
Pour vérifier que son budget est suffisant, il simule 100 fois le jeu d'un client à l'aide d'un logiciel.
On appelle $X$ la variable aléatoire qui, à $100$ jeux simulés, associe le nombre de bons d'achat gagnés.
On admet que $X$ suit une loi binomiale.
1. Préciser les paramètres de $X.$
2. Calculer la probabilité pour qu'il y ait exactement $30$ clients gagnants.
3. Quel est le montant moyen de la somme totale offerte en bons d'achat ?
Le budget prévisionnel est-il suffisant ?
Partie C
La direction de l'hypermarché étudie le temps que les clients passent dans son magasin.
On admet que le temps, exprimé en minute, passé dans ce magasin par un client peut être modélisé par une variable aléatoire $Y$ qui suit la loi normale d'espérance $\mu=45$ et d'écart type $\sigma=5.$
1. Calculer la probabilité qu'un client pris au hasard dans ce magasin reste entre $30$ et $60$ minutes.
2. Calculer la probabilité qu'un client pris au hasard dans ce magasin reste plus de $50$ minutes.
Exercice 2 (5 points)
Candidats de E, S n'ayant pas suivi l'enseignement de spécialité et candidats de L
Un infographiste simule sur ordinateur la croissance d'un bambou.
Il prend pour modèle un bambou d'une taille initiale de $1\,m$ dont la taille augmente d'un mois sur l'autre de $5\%$ auxquels s'ajoutent $20\,cm.$
Pour tout entier naturel $n$ non nul, on note un la taille, exprimée en centimètre, qu'aurait le bambou à la fin du $n-ième$ mois, et $u_{0}=100.$
1. Calculer $u_{1}$ et $u_{2}.$
2. Expliquer pourquoi, pour tout entier naturel $n$, $u_{n+1}=1.05\times u_{n}+20.$
3. Pour tout entier naturel $n$, on pose : $v_{n}=u_{n}+400.$
a. Montrer que la suite $(v_{n})$ est une suite géométrique dont on précisera la raison et le premier terme $v_{0}.$
b. Pour tout entier naturel $n$, exprimer $v_{n}$ en fonction de $n.$
c. En déduire que pour tout entier naturel $n$, $u_{n}=500\times 1.05^{n}-400.$
d. Calculer la taille du bambou, au centimètre près, à la fin du $7e$ mois.
4. On considère l'algorithme ci-dessous dans lequel $n$ est un entier naturel et $u$ est un nombre réel.
$$\boxed{u\leftarrow 100\\ n\leftarrow 0\\\text{Tant que }u<200\text{ faire}\\\quad u\leftarrow 1.05\times u+20\\\quad n\leftarrow n+1\\\text{Fin Tant que}}$$
a. Recopier et compléter le tableau ci-dessous en ajoutant autant de colonnes que nécessaire pour retranscrire l'exécution de l'algorithme.
$$\begin{array}{|c|c|c|c|c|} \hline \text{Test }u<200& &\text{vrai}& &\ldots\\ \hline \text{Valeur de }u&100& & &\ldots\\ \hline \text{Valeur de }n&0& & &\ldots\\ \hline \end{array}$$
b. Quelle est la valeur de la variable $n$ à la fin de l'exécution de l'algorithme ?
Interpréter le résultat au regard de la situation étudiée dans cet exercice.
c. Modifier les lignes nécessaires dans l'algorithme pour déterminer le nombre de mois qu'il faudrait à un bambou de $50\,cm$ pour atteindre ou dépasser $10\,m.$
Exercice 2 (5 points)
Candidats de E, S ayant suivi l'enseignement de spécialité
La mairie d'une ville propose une carte jeune annuelle donnant droit à des réductions sur les activités culturelles et de loisirs.
La mairie espère que dans l'avenir, au moins $70\%$ de la population des $12-18\,ans$ possèdent la carte et si oui, en quelle année cela se produirait.
Ces dernières années, lors du renouvellement de la carte, on a constaté que $10\%$ des possesseurs de la carte ne la rachètent pas.
Dans le même temps, $30\%$ de la population des $12-18\,ans$ qui ne la possédaient pas l'année précédente achètent la carte.
On fait l'hypothèse que l'effectif de la population des $12-18\,ans$ est constant et que l'évolution va rester la même pour les prochaines années.
En $2018$, $80\%$ des jeunes de $12-18\,ans$ ne possédaient pas la carte.
On note, pour tout entier naturel $n$, $a_{n}$ la part de la population des $12-18\,ans$ de la ville possédant la carte l'année $2018+n$ et $b_{n}$ la part de la population des $12-18\,ans$ ne la possédant pas.
Partie A
1. Représenter cette situation par un graphe probabiliste de sommets $A$ et $B$ où le sommet $A$ représente l'état « posséder une carte jeune » et $B$ l'état « ne pas posséder une carte jeune ».
2. Déterminer la matrice de transition $M$ de ce graphe en respectant l'ordre $A$ puis $B$ des sommets.
3. a. Vérifier que $a_{2}=0.552$ et $b_{2}=0.448.$
b. Interpréter le coefficient $0.552$ dans le contexte de l'énoncé.
4. On note $a$ et $b$ les coefficients de la matrice $P$ correspondant à l'état stable de ce graphe.
a. Montrer que les nombres $a$ et $b$ sont solutions du système
$$\left\lbrace\begin{array}{rcl} -0.1 a+0.3b&=&0\\ a+b&=&1 \end{array}\right.$$
b. Justifier que la mairie peut espérer qu'à l'avenir au moins $70\%$ de la population des $12-18\,ans$ possèdent la carte.
Partie B
On admet que pour tout entier naturel $n$, $a_{n+1}=0.6a_{n}+0.3$ et que la suite $(a_{n})$ est croissante.
1. On donne l'algorithme suivant dans lequel $A$ est un nombre réel et $N$ est un entier naturel
$$\boxed{A\leftarrow 0.2\\ N\leftarrow 0\\\text{Tant que }\ldots\text{faire}\\\quad A\text{ prend la valeur}\ldots\\\quad N\text{ prend la valeur}\ldots\\\text{Fin Tant que}}$$
Recopier puis compléter les pointillés des lignes $3$ à $5$ de l'algorithme ci-dessus pour qu'il affiche le nombre d'années nécessaires à la mairie pour atteindre son objectif qu'au moins $70\,%$ de la population des $12-18\,ans$ possèdent la carte.
2. En quelle année l'objectif sera-t-il atteint ?
Exercice 3 (7 points)
Commun à tous les candidats
Dans la figure ci-dessous sont représentés dans un repère orthogonal :
$-\ $ la courbe $\mathfrak{C}$ représentative d'une fonction $f$ définie sur l'intervalle $[-10\ ;\ 5]$
$-\ $ La tangente $T$ à $\mathfrak{C}$ au point $A$ d'abscisse $-5$
$-\ $ La droite $\mathfrak{D}$ d'équation $y=x$ ;
$-\ $ Le domaine $S$ situé entre la droite $\mathfrak{D}$ et la courbe $\mathfrak{C}$, grisé sur la figure.
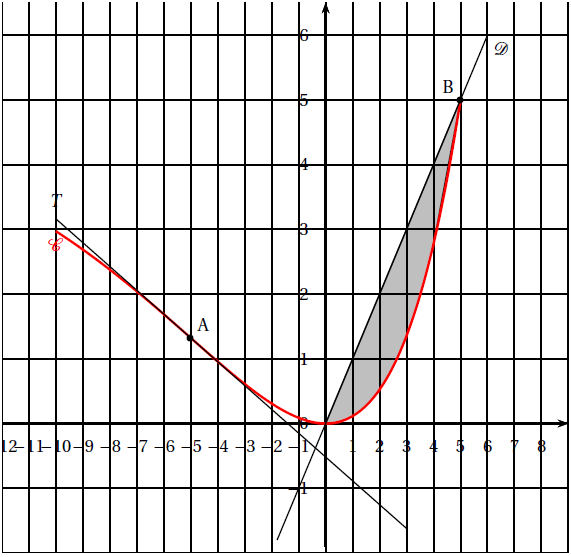
Partie A
Dans cette partie les estimations seront obtenues par lecture graphique.
Cette partie $A$ est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Aucune justification n'est demandée.
Une bonne réponse rapporte un point.
Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la réponse correspondante.
1. Parmi les quatre valeurs ci-dessous, la meilleure valeur approchée du coefficient directeur de la tangente $T$ est :
a. $-\dfrac{1}{3}$
b. $-3$
c. $3$
d. $\dfrac{1}{3}$
2. La fonction $f$ semble :
a. concave sur $[-5\ ;\ 0]$
b. concave sur $[-10\ ;\ 0]$
c. convexe sur $[-10\ ;\ 5]$
d. convexe sur $[-5\ ;\ 5]$
3. L'aire du domaine $S$, en unité d'aire, appartient à l'intervalle :
a. $[-4\ ;\ −2]$
b. $[4\ ;\ 7]$
c. $[0\ ;\ 3]$
d. $[7\ ;\ 10]$
Partie B
La fonction $f$ précédente, définie et dérivable sur l'intervalle $[-10\ ;\ 5]$, a pour expression
$$f(x)=(x-5)\mathrm{e}^{0.2x}+5.$$
1. On note $f'$ la fonction dérivée de $f$ sur l'intervalle $[-10\ ;\ 5].$
a. Montrer que $f'(x)=0.2x\mathrm{e}^{0.2x}.$
b. Dresser le tableau de variation de la fonction $f$ sur l'intervalle $[-10\ ;\ 5].$
c. Déterminer la valeur exacte du coefficient directeur de la tangente $T$ à $\mathfrak{C}$ au point $A$ d'abscisse $-5.$
2. Un logiciel de calcul formel donne les résultats suivants :
$$\begin{array}{|c|l|} \hline 1&g(x)=0.2x\ast\text{ exp}(0.2x)\\ &\rightarrow g(x)=\dfrac{1}{5}x\mathrm{e}^{\dfrac{1}{5}x}\\ \hline 2&\text{Dérivée }g'(x)=\dfrac{1}{25}x\mathrm{e}^{\dfrac{1}{5}x}+\dfrac{1}{5}\mathrm{e}^{\dfrac{1}{5}x}\\ \hline \end{array}$$
a. En utilisant ces résultats, justifier que la dérivée seconde de $f$, notée $f''$, est définie par :
$$f''(x)=(0.2+0.04x)\mathrm{e}^{0.2x}.$$
$$f''(x)=(0.2+0.04x)\mathrm{e}^{0.2x}.$$
b. Étudier la convexité de la fonction $f$ sur l'intervalle $[-10\ ;\ 5].$
3. On admet qu'une primitive de $f$ sur l'intervalle $[-10\ ;\ 5]$ est la fonction $F$ définie par :
$$F(x)=(5x-50)\mathrm{e}^{0.2x}+5x.$$
$$F(x)=(5x-50)\mathrm{e}^{0.2x}+5x.$$
a. Déterminer la valeur exacte de $I$ définie par :
$$I=\int_{0}^{5}f(x)\mathrm{d}x.$$
$$I=\int_{0}^{5}f(x)\mathrm{d}x.$$
b. Montrer que l'aire du domaine du plan situé sous la droite $\mathfrak{D}$, au-dessus de l'axe des abscisses et limité par la droite d'équation $x=5$ vaut $12.5$ unités d'aire.
c. En déduire une valeur approchée de l'aire du domaine $S$ en unité d'aire.
Exercice 4 (3 points)
Commun à tous les candidats
Afin de respecter l'accord signé sur la pollution de l'air, certaines entreprises, dès l'année $2014$, ont été contraintes de diminuer chaque année la quantité de $CO_{2}$ qu'elles produisent.
Une de ces entreprises émettait $15$ milliers de tonnes de $CO_{2}$ en $2014$ et $14.7$ milliers de tonnes en $2015.$
On suppose que le taux de diminution annuel de $CO_{2}$ émis restera constant pendant les années suivantes.
1. Calculer le taux d'évolution de l'émission de $CO_{2}$ par cette entreprise entre $2014$ et $2015.$
2. L'accord prévoit que cette entreprise devra produire moins de $12$ milliers de tonnes de $CO_{2}$ par an.
En détaillant la méthode employée, déterminer à partir de quelle année la quantité de $CO_{2}$ émise par cette entreprise passera en dessous de ce seuil de $12$ milliers de tonnes.
$$\text{Durée : }3\,heures$$

Ajouter un commentaire