Bac Maths, ES/L - Asie - 20 juin 2019
Exercice 1 (4 points)
Commun à tous les candidats.
Cet exercice est un questionnaire à choix multiples.
Chaque question comporte quatre réponses possibles.
Pour chacune de ces questions, un seule des quatre réponses proposées est exacte.
Recopier pour chaque question son numéro et la lettre correspondant à la réponse choisie.
Aucune justification n'est demandée.
Chaque réponse exacte rapporte 1 point, une mauvaise réponse ou l'absence de réponse ne rapporte ni n'enlève de point.
Pour tout évènement $E$, on note $p(E)$ sa probabilité.
1) Soit $X$ la variable aléatoire suivant la loi binomiale $\mathfrak{B}(20\ ;\ 0.4).$
a) $p(X=7)=20\times 0.4^{7}.$
b) $p(X>4)=0.98$ arrondie au centième
c) $p(X\leq 4)=0.05$ arrondie au centième
d) $p(X\leq 7)=0.25$ arrondie au centième
2) L'équation $(\mathrm{e^{x}})^{2}=3\mathrm{e}^{x}$ possède :
a) une unique solution $3$
b) une unique solution $\ln(3)$
c) deux solutions $0$ et $\ln(3)$
d) deux solutions $0$ et $3$
3) Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\dfrac{x}{\mathrm{e^{x}}}.$
Une autre expression de $f(x)$ est :
a) $f(x)=\dfrac{\mathrm{e^{-x}}}{-x}$
b) $f(x)=-x\mathrm{e^{-x}}$
c) $f(x)=\dfrac{\mathrm{e^{-x}}}{x}$
d) $f(x)=x\mathrm{e^{-x}}$
4) Soit $X$ une variable aléatoire suivant une loi normale dont la densité de probabilité est représentée ci-contre.
Sur le graphique, la surface grisée correspond à une probabilité de $0.95.$
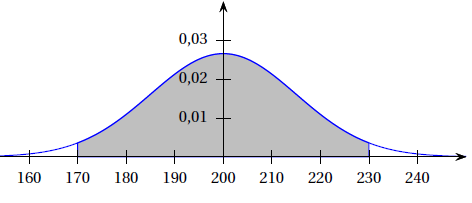
Une valeur approchée à $0.1$ près du nombre $\alpha$ tel que $p(X>\alpha)=0.1$ est :
a) $\alpha\simeq 180.8$
b) $\alpha\simeq 212.6$
c) $\alpha\simeq 219.2$
d) $\alpha\simeq 238.4$
Exercice 2
Commun à tous les candidats
Les parties $A$, $B$ et $C$ sont indépendantes.
Si nécessaire, les résultat seront arrondis au centième.
Partie A
Un club de football est composé d'équipes adultes masculines, adultes féminines et d'équipes d'enfants.
Chaque week-end, la présidente Claire assiste au match d'une seule des équipes du club et elle suit :
$\bullet\ $ dans $10\%$ des cas, le match d'une équipe adulte féminine ;
$\bullet\ $ dans $40\%$ des cas, le match d'une équipe adulte masculine ;
$\bullet\ $ dans les autres cas, le match d'une équipe d'enfants.
Lorsqu'elle assiste au match d'une équipe masculine, la probabilité que celle-ci gagne est $0.6.$
Lorsqu'elle assiste au match d'une équipe d'enfants, la probabilité que celle-ci gagne est $0.54.$
La probabilité que Claire voie l'équipe de son club gagner est $0.58.$
On choisit un week-end au hasard.
On note les évènements suivants :
$\bullet\ $ $F$ : « Claire assiste au match d'une équipe adulte féminine » ;
$\bullet\ $ $M$ : « Claire assiste au match d'une équipe adulte masculine » ;
$\bullet\ $ $E$ : « Claire assiste au match d'une équipe d'enfants » ;
$\bullet\ $ $G$ :« l'équipe du club de Claire gagne le match ».
Pour tous évènements $A$ et $B$, on note $\overline{A}$ l'évènement contraire de $A$, $p(A)$ la probabilité de $A$ et, si $B$ est de probabilité non nulle, $p_{B}(A)$ la probabilité de $A$ sachant $B.$
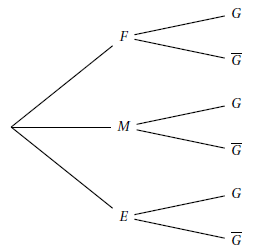
1) L'arbre de probabilité est donné en annexe 1.
Le compléter au fur et à mesure de l'exercice.
2) Déterminer la probabilité $p(M\cap G).$
3) a) Démontrer que $(F\cap G)=0.07.$
b) En déduire $p_{F}(G).$
c) La probabilité que l'équipe adulte féminine gagne un match est $0.47.$
La présence de Claire semble-t-elle favoriser la victoire de l'équipe adulte féminine ?
4) Claire annonce avoir assisté à la victoire d'une équipe du club.
Quelle est la probabilité qu'elle ait suivi le match d'une équipe adulte féminine ?
Partie B
Au guichet, un supporter attend pour acheter son billet.
On modélise le temps d'attente en minute par une variable aléatoire $X$ qui suit la loi normale d'espérance $\mu=30$ et d'écart-type $\sigma=10.$
1) En moyenne, combien de temps attend ce supporter au guichet ?
2) Déterminer $p(25\leq X\leq 35).$
Interpréter dans le contexte de l'exercice.
3) Le supporter ne dispose que de $15$ minutes avant le début du match pour acheter son billet
Quelle est la probabilité qu'il puisse acheter son billet avant le début du match ?
Partie C
Des études statistiques ont montré que la probabilité qu'un enfant se réinscrive d'une année sur l'autre dans le même club de football est $0.6.$
1) Déterminer l'intervalle de fluctuation asymptotique au seuil de $95\%$ de la proportion d'enfants se réinscrivant d'une année sur l'autre pour un échantillon de $75$ enfants pris au hasard dans le même club de football.
2) $52$ des $75$ enfants du club de Claire veulent se réinscrire en septembre $2018.$
La victoire de la France aux championnats du monde en $2018$ a-t-elle eu un effet sur les réinscriptions en septembre $2018$ dans ce club ?
Justifier.
Exercice 3
Candidats de E, S n'ayant pas suivi la spécialité et candidats de L
Les partie $A$ et $B$ sont indépendantes.
Partie A
Tous les ans, au mois de septembre, Richard prélève $8.5$ tonnes d'algues sur les plages de sa commune.
Au $1^{er}$ septembre $2018$, il y avait $230$ tonnes d'algues sur ces plages.
Tous les ans, entre le $1^{er}$ octobre et le $1^{er}$ septembre suivant, la quantité d'algues sur ces plages augmente de $4\%.$
On note un la quantité en tonnes d'algues présente sur les plages au $1^{er}$ septembre de l'année $2018+n.$
Ainsi, $u_{0}=230.$
1) Vérifier par le calcul que Richard disposera de $230.36$ tonnes sur les plages au $1^{er}$ septembre $2019$
On admet que, pour tout $n\in\mathbb{N}$, $u_{n+1}=1.04u_{n}-8.84.$
2) Soit $(v_{n})$ la suite définie par, pour tout $n\in\mathbb{N}$, $v_{n}=u_{n} -221.$
a) Démontrer que $(v_{n})$ est une suite géométrique de raison $1.04.$ Préciser son premier terme.
b) Exprimer, pour tout $n\in\mathbb{N}$, $v_{n}$ en fonction de $n.$
c) En déduire que, pour tout $n\in\mathbb{N}$, $u_{n}=221+9\cdot 1.04n.$
3) La quantité d'algues présentes sur ces plages dépassera-t-elle un jour $250$ tonnes ?
Si oui, préciser au bout de combien d'années cette quantité sera atteinte.
Partie B
Pour développer son entreprise, à partir du $1^{er}$ septembre $2019$, Richard a besoin de $10\%$ d'algues de plus que l'année précédente.
On rappelle qu'au $1^{er}$ septembre $2018$, il disposait de $230$ tonnes d'algues et qu'il en avait consommé $8.5$ tonnes en septembre $2018.$
Dans cette nouvelle situation, il disposera de $230.36$ tonnes d'algues au $1^{er}$ septembre $2019$ et en utilisera $9.35$ tonnes pendant ce mois.
Richard souhaite étudier la quantité d'algues sur les plages concernées pour les $16$ prochaines années selon ce modèle.
Pour cela il rédige l'algorithme ci-dessous.
$$\boxed{A\leftarrow 230\\\\B\leftarrow 8.5\\\\\text{Pour }K\text{ allant de }1\text{à }16\\\\A\leftarrow(A\leftarrow-B)\times 1.04\\\\B\leftarrow B\times 1.1\\\\\text{Fin pour}}$$
1) Que représentent les variables $A$ et $B$ de l'algorithme ?
2) Dans le tableau en annexe 2, on a obtenu différentes valeurs de $A$ et $B$ de l'algorithme.
Compléter les lignes du table au pour les valeurs de $K=1$ et $K=2.$
Arrondir les résultats au centième.
3) Que peut conclure Richard pour $2034$ ?
Exercice 3 (5 points)
Candidats de ES ayant suivi la spécialité
Une compagnie aérienne a représenté à laide d'un graphe les différentes liaisons assurées par ses avions.
Les sommets du graphe sont les initiales des aéroports desservis et les arêtes correspondent aux vols effectués par un avion de cette compagnie entre deux aéroports.
Par exemple, l'arête entre $A$ et $G$ signifie qu'un avion effectue le vol entre les aéroports $A$ et $G$, en partant de $A$ vers $G$ ou en partant de $G$ vers $A$.
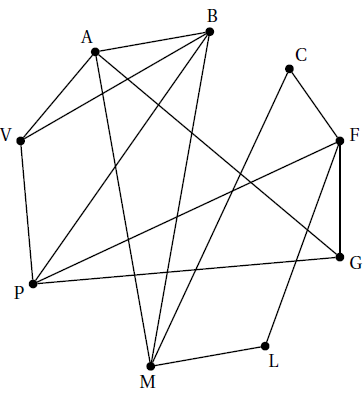
1) Le graphe est-il complet ?
Interpréter ce résultat dans le cadre de l'exercice.
2) On note $M$ la matrice d'adjacence du graphe ci-dessus en classant les sommets par ordre alphabétique.
Compléter les deux lignes manquantes de la matrice $M$ donnée en annexe 2.
3) La compagnie souhaite qu'un avion partant de l'aéroport $F$ effectue $3$ vols avant d'arriver à l'aéroport
À l'aide de la matrice $M^{3}$ donnée ci-dessous, déterminer le nombre de trajets possibles
$$M^{3}=\begin{pmatrix} 4&9&2&5&8&2&8&4&9\\ 9&6&2&5&4&2&8&9&7\\ 2&2&0&6&2&0&6&2&3\\ 5&5&6&2&6&6&2&7&3\\ 8&4&2&6&2&2&4&8&3\\ 2&2&0&6&2&0&6&2&3\\ 8&8&6&2&4&6&2&6&3\\ 4&9&2&7&8&2&6&4&8\\ 9&7&3&3&3&3&3&8&4 \end{pmatrix}$$
4) L'entreprise souhaite qu'un même avion puisse parcourir successivement une fois et une seule chaque liaison.
a) Justifier qu'un avion peut le faire et préciser les aéroports de départ et d'arrivée possibles.
b) Lors de ce trajet, combien de fois cet avion doit-il se poser à l'aéroport $P$ ?
Expliquer la réponse.
Partie B
Sur le graphe ci-dessous sont indiqués les différents temps de vol en heure entre deux aéroports.
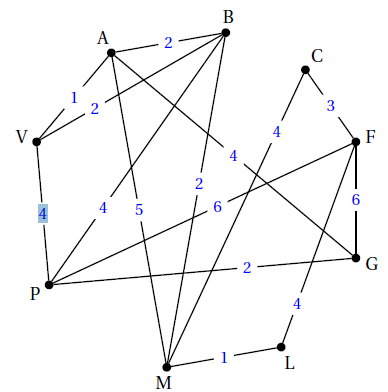
Un client souhaite utiliser une offre promotionnelle de cette compagnie pour voyager de l'aéroport $V$
jusqu'à l'aéroport $F.$
Combien d'heures de vol doit-il envisager au minimum?
Préciser le trajet.
Exercice 4 (5 points)
Commun à tous les candidats
On a représenté ci-contre la courbe $\mathcal{C}$ représentative d'une fonction $f$ définie et dérivable sur $[0.5\ ;\ 12]$, la tangente $T_{1}$ à $\mathcal{C}$ au point $A$ d'abscisse $1$ et la tangente $T_{2}$ à $\mathcal{C}$ au point $B$ d'abscisse
2) La tangente $T_{1}$ est parallèle à l'axe des abscisses.
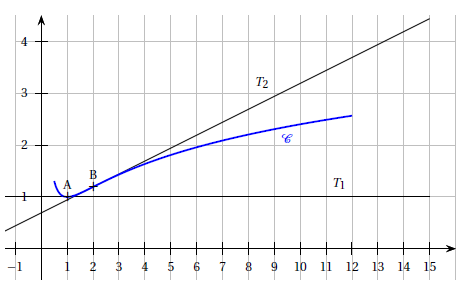
1) Par lecture graphique
a) Déterminer $f'(1).$
b) Déterminer les éventuels points d'inflexion de $\mathcal{C}.$
c) Déterminer un encadrement de $$\int_{6}^{8}f(x)\mathrm{d}x$$ par deux entiers consécutifs.
2) On admet que la fonction $f$ est définie sur $[0.5\ ;\ 12]$ par : $f(x)=\ln(x)+\dfrac{1}{x}.$
a) Vérifier que, pour tout $x\in[0.5\ ;\ 12]$, $f'(x)=\dfrac{x-1}{x^{2}}.$
b) Déterminer le signe de $f'(x)$ et en déduire le tableau de variations de $f.$
Si nécessaire, on arrondira à $0.1$ les valeurs numériques.
3) À l'aide d'un logiciel de calcul formel, on a obtenu les résultats suivants que l'on pourra admettre.
$$\begin{array}{|l|l|} \hline &\text{Calcul formel}\\ \hline 1&g(x)=(x-1)\setminus x^{2}\\\\&g(x)=\dfrac{x-1}{x^{2}}\\ \hline 2&\text{Dérivée }g(x)\\\\&g(x)=\dfrac{x^{2}-2x(x-1)}{x^{4}}\\ \hline 3&\text{Simplifier Dérivée }g(x)\\\\&g(x)=\dfrac{-x+2}{x^{3}}\\ \hline \end{array}$$
Déterminer par le calcul le plus grand intervalle sur lequel $f$ est concave.
4) Soit $F$ la fonction définie sur $[0.5\ ;\ 12]$ par $F(x)=(x+1)\ln(x)-x.$
a) Vérifier que $F$ est une primitive de $f$ sur $[0.5\ ;\ 12].$
b) En déduire la valeur exacte puis la valeur arrondie au centième de la valeur moyenne de $f$ sur l'intervalle $[0.5\ ;\ 12].$
Annexes à rendre avec la copie
Annexe 1
Exercice 2
Annexe 2
Exercice 3
Candidats de ES n'ayant pas suivi la spécialité ou candidats de L
Valeurs de $A$ et $B$ obtenues à l'aide d'un tableur
$$\begin{array}{|c|c|c|} \hline K&A&B\\ \hline &230&8.5\\ \hline 1& &\\ \hline 2& &\\ \hline 3&228.35&11.31\\ \hline 4&225.72&12.44\\ \hline 5&221.80&13.69\\ \hline 6&216.44&15.06\\ \hline 7&209.43&16.56\\ \hline 8&200.58&18.22\\ \hline 9&189.66&20.04\\ \hline 10&176.40&22.05\\ \hline 11&160.53&24.25\\ \hline 12&141.73&26.68\\ \hline 13&119.65&29.34\\ \hline 14&93.92&32.28\\ \hline 15&64.11&35.51\\ \hline 16&29.75&39.06\\ \hline \end{array}$$
Annexe 2
Exercice 3
Candidats de ES ayant suivi la spécialité
$$M=\begin{pmatrix} 0&1&0&0&1&0&1&0&1\\ \ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\ \ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\ 0&0&1&0&1&1&0&1&0\\ 1&0&0&1&0&0&0&1&0\\ 0&0&0&1&0&0&1&0&0\\ 1&1&1&0&0&1&0&0&0\\ 0&1&0&1&1&0&0&0&1\\ 1&1&0&0&0&0&0&1&0 \end{pmatrix}$$

Ajouter un commentaire