Bac Maths, ES/L Nouvelle Calédonie 26 novembre 2019

Commun à tous les candidats

Cet exercice est un questionnaire à choix multiples.

Chaque question comporte quatre réponses possibles.

Pour chacune de ces questions, une seule des quatre réponses proposées est exacte.

Recopier pour chaque question son numéro et la lettre correspondant à la réponse choisie.

Aucune justification n'est demandée.

Chaque réponse exacte rapporte 1 point, une mauvaise réponse ou l'absence de réponse ne rapporte ni n'enlève de point.

1) Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=−0.9x^{3}+1.5x^{2}+1.5$ et $\mathcal{C}$ sa courbe représentative dans un repère.

Le nombre de points d'intersection entre la courbe $\mathcal{C}$ et la droite d'équation $y=2$ est :

a) $0$

b) $1$   

c) $2$    

d) $3$

2) Une des solutions de l'inéquation $1−0.85^{n}>0.99$ d'inconnue $n$ entier naturel est :

a) $28$   

b) $29$  

c) $\dfrac{\ln 0.85}{\ln 0.01}$

d) $28.3363$

Esteban va à l'école chaque matin avec une trousse.

À la fin de la journée, il oublie sa trousse avec une probabilité de $0.2$.

Dans l'année le nombre de jours d'école est de $162.$

On considère que les oublis journaliers sont indépendants les uns des autres.

La probabilité qu'il oublie sa trousse $30$ fois exactement dans l'année est environ :

a) $0.19$

b) $0.07$

c) $0.60$

d) $0.364$

Une enquête a pour objectif d'estimer la proportion de personnes partant en vacances à l'étranger durant la semaine de Noël.

Pour obtenir un intervalle de confiance d'amplitude $0,001$ au niveau de confiance $0.95$ de cette proportion, la taille de l'échantillon doit être égale à :

a) $4\,000\,000$

b) $1\,000$   

c) $2\,000$     

d) $1\,000\,000$

Candidats de E, S n'ayant pas suivi l'enseignement de spécialité et candidats de L
 
Les parties A et B peuvent être traitées de manière indépendante.
 
Dans cet exercice, les résultats seront arrondis à l'unité.
 
Partie A
 
La responsable d'un aquarium public constate qu'en l'absence d'action particulière la population d'une espèce de poisson augmente de $20\%$ par an.

Pour démarrer un nouveau bassin, elle décide de prélever $28$ poissons à la fin de chaque année
 
La situation est modélisée par une suite$(u_{n})$ de terme initial $u_{0}=150$, le terme $u_{n}$ donnant une estimation du nombre de poissons au $1^{er}$ janvier de l'année $2018+n.$

1) Calculer $u_{1}$ et $u_{2}.$

2) Justifier que, pour tout $n\in\mathbb{N}\;,\ \ u_{n+1}=1.2u_{n}−28.$

3) On définit la suite $(w_{n})$ par : $w_{n}=u_{n}−140$ pour tout $n\in\mathbb{N}.$

a) Montrer que la suite$(w_{n})$ est une suite géométrique de raison $1.2.$

Préciser son terme initial.

b) Exprimer pour tout $n\in\mathbb{N}\;,\ w_{n}$ en fonction de $n.$

En déduireunen fonction de $n.$

4) Sachant que l’aquarium ne peut contenir plus de $200$ poissons, la responsable doit-elle prévoir l’achat d’un autre aquarium dans les années à venir ?

Si oui, en quelle année ? 

On sait qu’il y a eu $1350$ visiteurs le premier mois et que le prix d’entrée est fixé à $8$ euros.

La responsable fait l’hypothèse d’une augmentation mensuelle de la fréquentation des visiteurs de $12\%.$

Elle veut alors savoir, sous cette hypothèse, la recette totale accumulée durant les six pre-miers mois.

1) Recopier et compléter l’algorithme suivant pour qu’il détermine la recette cherchée.

$$\begin{array}{|c|} \hline S\leftarrow{0}\\ V\leftarrow{1350}\\ \text{Pour }N\text{ allant de }1\text{ à }\dots\\ \qquad S\leftarrow{\dots}\\ \qquad V\leftarrow{1.12}V\\ \text{Fin Pour}\\ S\leftarrow{8S}\\ \hline \end{array}$$

2) Quel est le montant de la recette cherchée?

Candidats de la série E, S ayant suivi l’enseignement de spécialitéLes parties A et B peuvent être traitées de manière indépendante.

Sur son lieu de vacances d’été, Inaé décide de pratiquer son activité favorite : le vélo tout terrain $(VTT).$

Le plan des sentiers $VTT$ de la région est représenté par le graphe ci-dessous.

Les arêtes représentent les sentiers, les sommets représentent les intersections de ces sentiers etle poids des arêtes désigne la distance en $km$ entre chaque intersection.

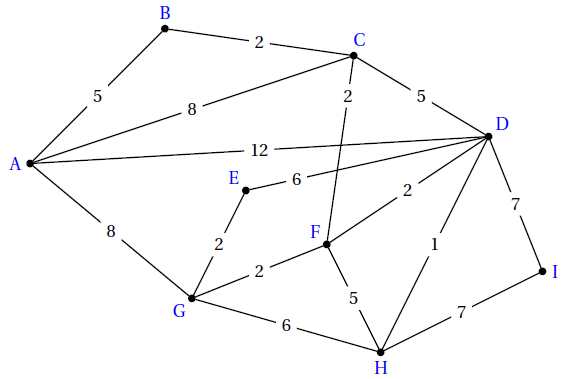
1) Pourra-t-elle explorer tous les sentiers en ne passant qu’une fois sur chacun d’entre eux ?

Justifier.

2) Inaé se trouve en $A$ et a rendez-vous au point $I.$

Elle veut s’y rendre en empruntant l’itinéraire le plus court.

Déterminer à l’aide d’un algorithme cet itinéraire en en préciser lalongueur.

En $2018$, des vélos électriques ont été mis en location.

Les clients ont donc eu le choix entre desvélos classiques et des vélos électriques.

En $2018$, seulement $10\%$ des clients ont loué des vélo sélectriques.

On admet que tous les clients louent un vélo et que :

$\bullet\ 85\%$des clients ayant loué un vélo électrique une année en relouent un l'année suivante ;

$\bullet\ 70\%$des clients ayant loué un vélo classique une année en relouent un l’année suivante.

On suppose que le nombre de clients chaque été reste constant.

On s'intéresse à la répartition des clients dans les années à venir.

On note pour tout entier naturel $n$ :

$\bullet\ c_{n}$la probabilité qu'un client pris au hasard choisisse un vélo classique l'année $2018+n$ ;

$\bullet\ e_{n}$la probabilité qu'un client pris au hasard choisisse un vélo électrique l'année $2018+n$ ;

$\bullet\ P_{n}=(c_{n}\quad e_{n})\ $la matrice correspondant à l'état probabiliste l'année $2018+n.$

1) Représenter la situation par un graphe probabiliste.

On notera $\mathcal{C}$ l'évènement « le client loue un vélo classique» et $E$ l'évènement « le client loue $u_{n}$ vélo électrique ».

2) Donner la matrice $P_{0}$ traduisant l'état probabiliste initial ainsi que la matrice de transition $M$ en respectant l'ordre $C$ puis $E$ des sommets.

3) Calculer $P_{1}.$

4) Déterminer l'état stable du graphe probabiliste et interpréter le résultat obtenu dans le $c$ on texte de l'exercice.

Commun à tous les candidats 

Les parties A, B et C peuvent être traitées de manière indépendante.Les résultats seront arrondis au centième.

Lors d'un safari photo en Afrique, un groupe de touristes souhaite observer des familles d'éléphants.

Le guide leur explique que :

$\bullet\ $la probabilité de voir des éléphants adultes dans la journée est de $0.85$ ;

$\bullet\ $la probabilité de voir des bébés éléphants sachant que l'on voit des éléphants adultes est de $0.5$ ;

$\bullet\ $la probabilité d'observer des bébés éléphants mais pas d'adultes éléphants dans la journée est de $0.015.$

On choisit au hasard un touriste de ce groupe et on considère les évènements suivants :

$A$ : « Le touriste voit des éléphants adultes dans la journée » ;

$B$ : « Le touriste voit des bébés éléphants dans la journée ».

Pour tous évènements $E$ et $F$, on note $\overline{E}$ l'évènement contraire de $E$, $p(E)$ la probabilité de $E$ et, si $F$ est de probabilité non nulle, $p_{F}(E)$ la probabilité de $E$ sachant $F.$

1) Donner $p\left(\overline{A}\cap B\right).$

2) Représenter la situation à l'aide d'un arbre pondéré qui sera complété au fur et à mesure de l'exercice.

3) Montrer que $p(B)=0.44.$

4) a) Calculer $p_{\overline{A}}(B).$

b) Interpréter ce résultat dans le contexte de l'exercice.

À $20\ h$, le groupe de touristes fait une pause autour d'un point d'eau pour observer le bain des éléphants.

On considère que le temps d'attente en minute nécessaire pour observer des éléphants suit la loi uniforme sur l'intervalle $[0\ ;\ 90].$

1) Quelle est la probabilité que le groupe attende plus d'une heure avant d'apercevoir les éléphants ?

2) Calculer l'heure moyenne d'arrivée des éléphants.

Lors de leur séjour, les touristes ont appris que les éléphants d'Afrique sont généralement plus grands que les éléphants d'Asie.

On modélise la taille en centimètre d'un éléphant d'Afrique par une variable aléatoire $X$ suivant la loi normale de moyenne $\mu$ et d'écart type $\sigma.$

De même, on modélise la taille en centimètre d'un éléphant d'Asie par une variable aléatoire $Y$ suivant une loi normale de moyenne $\mu'$ et d’écart type $\sigma'.$

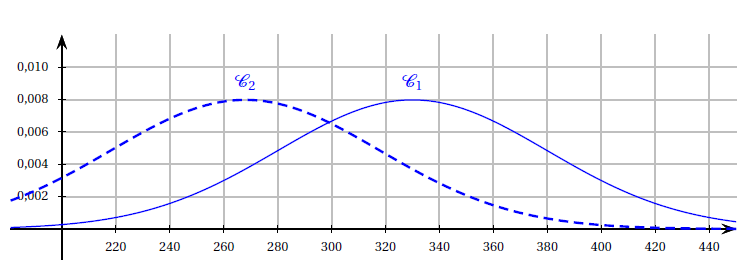
Les courbes $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$, des densités de probabilité associées à $X$ et $Y$  sont données en annexe 1.

1) a) Associer chaque courbe $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$ à sa variable aléatoire.

b) Donner une valeur approchée à la dizaine de l'espérance pour chacune d'entre elles.

2) Représenter graphiquement $p(X>330)$ et $p(Y>330)$ puis comparer ces deux probabilités.

3) a) Calculer à l'aide de la calculatrice $p(Y>330)$ sachant que $\mu=268$ et $\sigma′=50.$

b) Interpréter ce résultat dans le contexte de l'exercice.

Commun à tous les candidats 

On considère la fonction $f$ définie sur $\mathbb{R}$ par :
$$f(x)=(−5x^{2}+5)\mathrm{e}^{x}$$

On note $f′$ la fonction dérivée de $f$, et $f′′$ la fonction dérivée seconde.

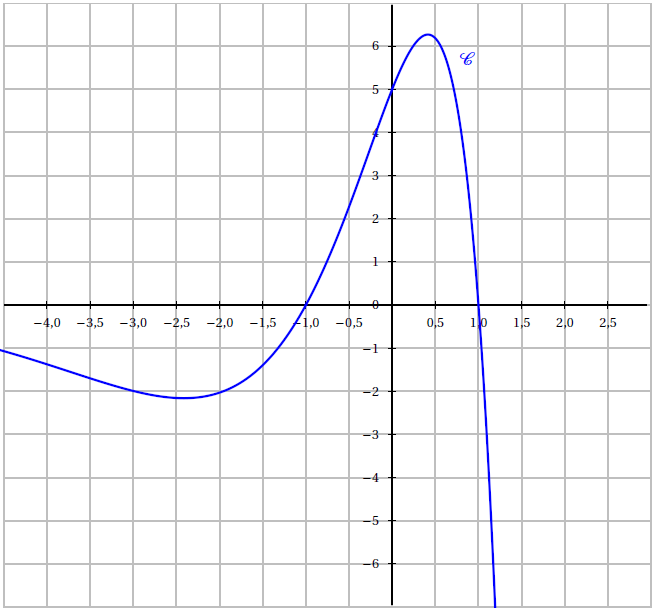
On note $\mathfrak{C}$ la courbe représentative de la fonction $f$ dans un repère du plan, donnée en annexe 2.

1) a) Calculer les coordonnées du point $A$, intersection de la courbe $\mathcal{C}$ avec l'axe des ordonnées.

Placer le point $A$ dans le repère fourni en annexe

2) b) Démontrer que $\mathcal{C}$ coupe l'axe des abscisses en deux points.

Déterminer leurs coordonnées et les placer dans le repère fourni en annexe 2.

c) Montrer que pour tout $x\in\mathbb{R}\;,\ f′(x)=(−5x^{2}−10x+5)\mathrm{e}^{x}.$

d) Étudier les variations de la fonction $f$ sur l'intervalle $[-5\ ;\  2].$

2) Soit $\Delta$ la tangente à $\mathcal{C}$ au point d'abscisse $0.$

a) Montrer qu'une équation de $\Delta$ est $y=5x+5.$

b) Tracer la droite $\Delta$ dans le repère fourni en annexe 2.

3) Un logiciel de calcul formel donne les résultats suivants que l'on pourra utiliser sans justification.

$$\begin{array}{|c|l|} \hline 1& f (x)\\ \circ&\rightarrow(−5x^{2}+5)\mathrm{e}^{x }\\ \hline 2&f''(x)\\ \circ&\rightarrow -20x\mathrm{e}^{x}-5x^{2}\mathrm{e}^{x}-5\mathrm{e}^{x}\\ \hline 3&\text{Résoudre}(f ′′(x)=0.x)\\ \circ&\rightarrow\{x=-\sqrt{3}-2\;,\ x=\sqrt{3}-2\}\\ \hline \end{array}$$

a) Montrer que,pour tout $x\in[-5\ ;\ 2]\;,\ f ′′(x)=−(5x^{2}+20x+5)\mathrm{e}^{x}.$

b) Étudier la convexité de le fonction $f$ sur l'intervalle $[-5\ ;\ 2].$

4) On s'intéresse à l'aire $\mathcal{A}$, en unité d'aire,du domaine délimité par $\mathcal{C}$ ,l'axe des abscisses et les droites d'équation $x=-1$ et $x=0.$

a) Hachurer sur l'annexe 2 ce domaine.

b) On admet que sur l'intervalle $[-1\ ;\ 0]$, la droite $\Delta$ est au-dessus de la courbe $\mathcal{C}.$

Justifier que l'aire $\mathcal{A}$ est inférieure à $2.5$ unités d'aire. $\mathcal{C}.$
 
On admet que la fonction $F$ définie sur $\mathbb{R}$ par $F(x)=(−5x^{2}+10x−5)\mathrm{e}^{x}$ est une primitive de $f.$

Calculer $$\int^{0}_{−1} f (x)\mathrm{d}x.$$

On donnera la valeur exacte puis la valeur arrondie au centième.