Bac maths, Polynésie 4 mai 2022

 a.$\begin{array}{|c|} \hline def seuil() :\\ m=0\\ v=57 \\ while v < 200 : \\ m=m+1 \\ v = v*1.03 \\ return m\\ \hline \end{array}$

b.$\begin{array}{|c|} \hline def seuil() :\\ m=0 \\ v=57\\ while \\ v > 200 : \\ m=m+1 \\ v = v*1.03 \\ return m\\ \hline \end{array}$

c. $\begin{array}{|c|} \hline def seuil() : \\ v=57 \\ for i in range (200) : \\ v = v*1.03 \\ return v\\ \hline \end{array}$

d.$\begin{array}{|c|} \hline def seuil() : \\ m=0 \\ v=57 if v < 200 :\\ m=m+1 \\ else : \\ v = v*1.03 \\ return m\\ \hline \end{array}$

Selon les autorités sanitaires d’un pays, $7 %$ des habitants sont affectés par une certaine maladie.Dans ce pays, un test est mis au point pour détecter cette maladie. Ce test a les caractéristiques suivantes :

• Pour les individus malades, le test donne un résultat négatif dans $20%$ des cas;

• Pour les individus sains, le test donne un résultat positif dans $1%$ des cas.Une personne est choisie au hasard dans la population et testée.On considère les évènements suivants :

• $M$ « la personne est malade »;

• $T$ « le test est positif ».

1. Calculer la probabilité de l’évènement $M ∩T$ . On pourra s’appuyer sur un arbre pondéré.

2. Démontrer que la probabilité que le test de la personne choisie au hasard soit positif,est de$0,0653$.

3. Dans un contexte de dépistage de la maladie, est-il plus pertinent de connaître $P_{M} (T )$
ou $P_{T} (M)$ ?
4. On considère dans cette question que la personne choisie au hasard a eu un test positif. Quelle est la probabilité qu’elle soit malade ? On arrondira le résultat à $10^{−2}$ près.

5. On choisit des personnes au hasard dans la population. La taille de la population de ce pays permet d’assimiler ce prélèvement à un tirage avec remise.On note $X$ la variable aléatoire qui donne le nombre d’individus ayant un test positif parmi les $10$ personnes.

a. Préciser la nature et les paramètres de la loi de probabilité suivie par $X$.

b. Déterminer la probabilité pour qu’exactement deux personnes aient un test positif. On arrondira le résultat à $10^{−2}$ près.

6. Déterminer le nombre minimum de personnes à tester dans ce pays pour que la probabilité qu’au moins l’une d’entre elle ait un test positif, soit supérieur à $99%$.

Soit $(u_{n})$ la suite définie par $u_{0} = 1$ et pour tout entier naturel $n, u_{n+1} =\dfrac{u_{n}}{1+u_{n}}$.

1. a. Calculer les termes $u_{1}, u_{2}$ et $u_{3}$. On donnera les résultats sous forme de fractions irréductibles.

b. Recopier le script python ci-dessous et compléter les lignes $3$ et $6$ pour que liste$(k)$ prenne en paramètre un entier naturel $k$ et renvoie la liste des premières valeurs
de la suite $(u_{n})$ de $u_{0}$ à $u_{k}$.

$$\begin{array}{|c|c|} \hline 1.& def liste(k) :\\ \hline 2.& L = []\\ \hline 3.& u = ...\\ \hline 4.& for i in range(0, k+1) :\\ \hline 5.& L.append(u)\\ \hline 6.& u = ...\\ \hline 7.& return(L)\\ \hline \end{array}$$

2. On admet que, pour tout entier naturel $n, u_{n}$ est strictement positif.

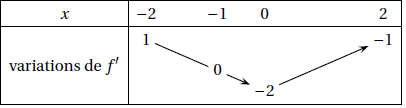
Déterminer le sens de variation de la suite $(u_{n})$.

3. En déduire que la suite $(u_{n})$ converge.

4. Déterminer la valeur de sa limite.

5. a. Conjecturer une expression de $u_{n}$ en fonction de $n$.

b. Démontrer par récurrence la conjecture précédente.

L’espace est rapporté un repère orthonormal où l’on considère :

• les points $A(2 ; −1 ; 0) B(1 ; 0 ; −3), C(6 ; 6 ; 1) et E(1 ; 2 ; 4)$;

• Le plan $\mathbb{P}$ d’équation cartésienne $2x − y − z +4 = 0$.

1. a. Démontrer que le triangle ABC est rectangle en $A$.

b. Calculer le produit scalaire $\vec{BA}$ ·\vec{BC}$puis les longueurs$BA$et$BC$.

c. En déduire la mesure en degrés de l’angle ABC arrondie au degré.

2. a. Démontrer que le plan P est parallèle au plan $ABC$.

b. En déduire une équation cartésienne du plan $ABC$.

c. Déterminer une représentation paramétrique de la droite $D$ orthogonale au plan $ABC$ et passant par le point $E$.

d. Démontrer que le projeté orthogonal $H$ du point $E$ sur le plan $ABC$ a pour coordonnées $(4;\dfrac{1}{3};\dfrac{5}{2})$.

3. On rappelle que le volume d’une pyramide est donné par $V =\dfrac{1}{3}$

Bh où B désigne l’aire d’une base et $h$ la hauteur de la pyramide associée à cette base.Calculer l’aire du triangle $ABC$ puis démontrer que le volume de la pyramide $ABCE$ est égal à $16,5$ unités de volume.