Bac Maths, S Amérique du Nord juin 2000

Le plan complexe est rapporté à un repère orthonormal $(O,\vec{u},\vec{v})$.
 
Dans tout l'exercice, $z$ est un nombre complexe non nul.
 
À tout point $M$ d'affixe $z$, on associe le point $M'$ d'affixe $z' =-~\dfrac{1}{z}$, puis le point $I$ milieu du segment $[MM']$. L'affixe de
$I$ est donc $\dfrac{1}{2}\left(z - \dfrac{1}{z}\right)$.
 
Note : les questions $\textbf{2, 3}$ et $\textbf{4}$ sont largement indépendantes.
 
1.a Donner une relation entre les modules de $z$ et $z'$.
       Donner une relation entre leurs arguments.
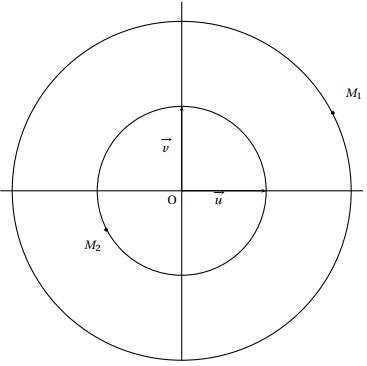
   b. Sur la figure ci-dessous est placé le point $M_1$ d'affixe $z_1$ sur le cercle de centre $O$ et de rayon $2.$
         Expliquer comment on peut obtenir géométriquement le point $M'_1$, puis le
         point $I_1$ milieu du segment $[M_1 M'_1]$. Effectuer cette construction.
 

    

 
2. Pour cette question, $\theta$ est un réel et $M$ est le point d'affixe $z = e^{\text{i}\theta}$.
     a. Calculer sous forme algébrique l'affixe de $I$.
     b. Sur la figure ci-dessous est placé le point $M_2$ d'affixe $z_2$ sur le
         cercle $\mathcal{C}$, de centre $O$ et de rayon $1.$

Expliquer comment, en utilisant le résultat de la question 2. a., on peut obtenir géométriquement le point $I_2$ milieu du segment $[M_2M'_2].$
        Effectuer cette construction.
Donner (sans justification) l'ensemble décrit par $I$ lorsque $M$ décrit $\mathcal{C}$.
   
3. Dans cette question, $M$ est un point du plan, distinct de $O.$
    a. Déterminer les points $M$ du plan complexe pour lesquels $M$ et $I$ sont confondus.
    b. Développer $(z - 2 \text{i})^2 + 3$.
          Déterminer les points $M$ du plan complexe pour lesquels l'affixe de $I$ est $2\mathrm{i}.$

4. Dans cette question, $M$ est un point du plan, distinct de $O$, d'affixe $z = x + \text{i}y~~(x$~et $y$ réels).
    a. Exprimer en fonction de $x$ et $y$ la partie réelle et la partie imaginaire de l'affixe de $I$.
    b. Déterminer l'ensemble $A$ des points $M$ du plan pour lesquels $I$ appartient à l'axe des abscisses.
    c. Déterminer l'ensemble $B$ des points $M$ du plan pour lesquels $I$ appartient  à l'axe des ordonnées.

Enseignement obligatoire
 

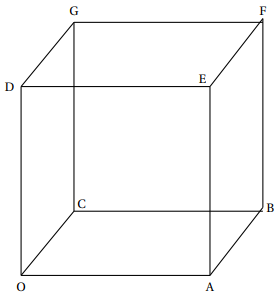
 Soit le cube $OABCDEFG$ représenté par la figure ci-dessus.

L'espace est orienté par le repère orthonormal direct $\left(\text{O}~ ;~\vec{\text{OA}},~\vec{\text{OC}},~\vec{\text{OD}}\right)$.

On désigne par $a$ un réel strictement positif.
 
$L,~ M$ et $K$ sont les points définis par $\vec{\text{O}L} = a\vec{\text{OC}},~ \vec{\text{O}M} = a\vec{\text{OA}}$, et $\vec{\text{B}K} = a \vec{\text{BF}}$.

1.
    a. Calculer les coordonnées du veceur $\vec{\text{D}M}\wedge \vec{\text{D}L}$.
    b. En déduire l'aire du triangle D$LM$.
    c. Démontrer que la droite $(OK)$ est orthogonale au plan $(DLM).$
    
2. On note $H$ le projeté orthogonal de $O$ et de $K$ sur le plan $(DLM).$

    a. Démontrer que $\vec{\text{O}M} \cdot \vec{\text{O}K} =\vec{\text{OH}} \cdot \vec{\text{OK}}$.
    b. Les vecteurs $\vec{\text{O}H}$ et $\vec{\text{O}K}$ étant colinéaires, on note $\lambda$ le réel tel que $\vec{\text{O}H} = \lambda\vec{\text{OK}}$.
        Démontrer que $\lambda = \dfrac{a}{a^2 + 2}$.
        En déduire que $H$ appartient au segment [O$K$].
    c. Déterminer les coordonnées de $H$.
    d. Exprimer $\vec{HK}$ en fonction de $\vec{\text{O}K}$. En déduire que $HK = \dfrac{a^2 - a + 2}{\sqrt{a^2 + 2}}$.
   
3. À l'aide des questions précédentes, déterminer le volume du tétraèdre $DLMK$ en fonction de $a.$

Enseignement de spécialité

Dans le plan orienté, on considère un triangle direct $OAB$, rectangle et isocèle en $O.$
 
On a donc $(\vec{\text{OA}},~\vec{\text{OB}}) = \dfrac{\pi}{2}~[2\pi]$.
 
On note $R_{\text{A}}$ et $R_{\text{B}}$ les rotations de centres respectifs

$A$ et $B$ et de même angle $\dfrac{\pi}{2}$ et $S_{\text{O}}$ la symétrie de centre $O.$
 
On place un point $C$, non situé sur la droite $(AB)$ , on trace les carrés

$BEDC$ et $ACFG$ directs.

On a donc $(\vec{\text{B}E},~\vec{\text{BC}}) = \dfrac{\pi}{2}~[2\pi]$ et$(\vec{\text{AC}},~ \vec{\text{A}G}) =\dfrac{\pi}{2}~[2\pi]$.
1.
    a. Déterminer S$_{(\text{AO})}\circ S_{(\text{AB})}$ composée des réflexions d'axes $(AB)$ et $(AO).$

    b. En écrivant $R_{\text{B}}$ sous la forme d'une composée de deux réflexions,
démontrer que $R_{\text{A}} \circ R_{\text{B}} = S_{\text{O}}$.

2.
     a. Déterminer l'image de $E$ par $R_{\text{A}} \circ R_{\text{B}}$.             
     b. En déduire que $O$ est le milieu du segment $[EG].$
     c. On note $R_{F}$ et $R_{D}$ les rotations de centres respectifs $F$ et $D$ et de même angle.
        Étudier l'image de C par la transformation $R_{F} \circ S_{\text{O}} \circ R_{D}$.
        Déterminer la transformation R$_{\text{F}} \circ S_{\text{O}} \circ R_{D}$.
    d. Placer $H$ le symétrique de $D$ par rapport à $O.$
         Démontrer que $R_{F}(H) = D$. Démontrer que le triangle $FOD$ est rectangle et isocèle en $O.$

 Soit $f$ la fonction définie sur $[0,~+~ \infty[$ par :
$$\left \{ \begin{array}{l c l } f(x) & = & \dfrac{x^2 + x + 1}{x^2}\text{e}^{-~\frac{1}{x}}~ \text{pour}~x > 0\\ f(0)& = &0. \end{array}\right.$$
On note $\mathcal{C}$ la courbe représentative de $f$ dans un repère orthonormal$(O,\vec{i}, \vec{j})$ (unité graphique 5~cm).

Partie A

1. Démontrer que la droite $(\Delta)$ d'équation $y = 1$ est asymptote à $\mathcal{C}$.
2. Pour $x > 0$ , calculer $\dfrac{f(x) - f(0)}{x}$. Étudier la limite de cette expression quand $x$ tend vers $0.$
   (on pourra utiliser, pour $n$ entier naturel non nul, $\displaystyle\lim_{u \to +~\infty} u^n\text{e}^{-u} = 0$.
    Que peut-on en déduire pour la fonction $f$ ? Que peut-on en déduire pour la courbe $\mathcal{C}$ ?
3. Démontrer que pour tout $x$ de $]0, +~ \infty[$ on a $f'(x) =\dfrac{1 - x}{x^4}\text{e}^{- \frac{1}{x}}$.
4. Étudier les variations de la fonction $f$ et dresser le tableau des variations de $f$.

Partie B

On note $g$ la fonction définie sur $]0~;~+ \infty[$ par $g(x) = f(x)-xf'(x)$.

1. Montrer que dans $]0~;~+ \infty[$, les équations $g(x) = 0$ et $x^3 + x^2 + 2x - 1 = 0$ sont équivalentes.
2. Démontrer que l'équation $x^3 + x^2 + 2x - 1 = 0$ admet une seule racine
réelle $\alpha$ dont on justifiera un encadrement à $10^{-~2}$ près.
3. On pose $A = \dfrac{f(\alpha)}{\alpha}$. Encadrer $A$ à $2 \times 10^{-~1}$ près (justifier) et montrer que $A = f'(\alpha)$.
4. Pour tout $a > 0$, on note $T_{a}$ la tangente à $\mathcal{C}$ au
point d'abscisse $a$.
Montrer que $T_{a}$ a pour équation $y = Ax$. Tracer $T_{a}$, puis la courbe $\mathcal{C}$.
5. Déduire des questions précédentes que de toutes les tangentes $T_{a}$ à $\mathcal{C}$ (en des points d'abscisses non nulles), seule $T_{\alpha}$ passe par l'origine $O.$
6. On admettra que $T_{\alpha}$ est au-dessus de $\mathcal{C}$ sur $]0~;~+\infty[$.
     a. Par lecture graphique (et sans justification), donner le nombre de solutions
de l'équation $f(x) = m$ , suivant le réel $m$ donné.
      b. Par lecture graphique (et sans justification), donner le nombre de solutions de l'équation $f(x) = mx$ selon le réel $m$ donné.
 
Partie C

1. Pour $n \in \mathbb{N}*$ on pose $u_{n} = \displaystyle\int_{\frac{1}{n}}^1 f(x)\:\text{d}x$. Sans calculer explicitement $u_{n}$, déterminer le signe de $u_{n+1} - u_{n}$. En déduire que la suite $(u_{n})$ est croissante.
2. Démontrer que la fonction $h$, définie sur $]0~;~+ \infty[$ par $h(x) = (x + 1)\text{e}^{-\frac{1}{x}}$ est une primitive de $f$ sur $]0~;~+\infty[$.
3. Calculer $u_{n}$. Interpréter graphiquement le résultat.
4. Étudier la convergence de la suite $\left(u_n\right)$.