Bac Maths, S Centre étrangers$^{1}$ 21 mars 2023

On considère la fonction $g$ définie sur l'intervalle $]0\ ;\ +\infty[$ par 

$$g(x)=\ln\left(x^{2}\right)+x-2$$

 

1. Déterminer les limites de la fonction $g$ aux bornes de son ensemble de définition.

 

2. On admet que la fonction g est dérivable sur l'intervalle $0\ ;\ +\infty[$

 

Étudier les variations de la fonction $g$ sur l'intervalle $]0\ ;\ +\infty[$

 

3.a. Démontrer qu'il existe un unique réel strictement positif α tel que $g(a)=0$

 

b. Déterminer un encadrement de $\alpha$ d'amplitude $10^{-2}$

 

4. En déduire le tableau de signe de la fonction $g$ sur l'intervalle $]0\ ;\ +\inf[$

On considère la fonction $f$ définie sur l'intervalle $]0\ ;\ +\infty[$ par :

$$f(x)=\dfrac{(x-2)}{x}\ln(x).$$

 

On note $\mathcal{C}_{f}$ sa courbe représentative dans un repère orthonormé.

 

1.a. Déterminer la limite de la fonction $f$ en $0.$

 

b. Interpréter graphiquement le résultat.

 

2. Déterminer la limite de la fonction $f$ en $+\infty.$

 

3. On admet que la fonction f est dérivable sur l'intervalle $]0\ ;\ +\infty[.$

 

Montrer que pour tout réel $x$ strictement positif, on a $f'(x)=\dfrac{g(x)}{x^{2}}$

 

4. En déduire les variations de la fonction $f$ sur l'intervalle $]0\ ;\ +\infty[$

Étudier la position relative de la courbe $\mathfrak{C}_{f}$ et de la courbe représentative de la fonction $\ln$ sur l'intervalle $]0\ ;\ +\infty[.$

Dans un souci de préservation de l'environnement, Monsieur Durand décide de se rendre chaque matin au travail en utilisant son vélo ou les transports en commun.

 

S'il choisit de prendre les transports en commun un matin, il reprend les transports en commun le lendemain avec une probabilité égale à $0.8$

 

S'il utilise son vélo un matin, il reprend son vélo le lendemain avec une probabilité égale à $0.4$

 

Pour tout entier naturel n non nul, on note :

 

$\bullet\ T_{n}$ l'évènement « Monsieur Durand utilise les transports en commun le $n$-ième jour »

 

$\bullet\ V_{n}$ l'évènement « Monsieur Durand utilise son vélo le $n$-ième jour »

 

$\bullet\ $On note $p_{n}$ la probabilité de l'évènement $T_{n}$, le premier matin, il décide d'utiliser les transports en commun. 

 

Ainsi, la probabilité de l'évènement $T_{1}$ est $P_{1}=1.$

 

1. Recopier et compléter l'arbre pondéré ci-dessous représentant la situation pour les $2^{e}$ et $3^{e}$ jours,

 

 

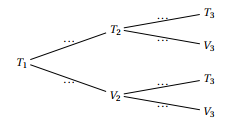
2. Calculer $p_{3}$

 

3. Le $3^{e}$ jour, M. Durand utilise son vélo.

 

Calculer la probabilité qu'il ait pris les transports en commun la veille.

 

4. Recopier et compléter l'arbre pondéré ci-dessous représentant la situation pour les $n$-ième et $(n+1)$ -ième jours

 

 

5. Montrer que, pour tout entier naturel $n$ non nul, $p_{n+1}=0.2p+0.6$

 

6. Montrer par récurrence que, pour tout entier naturel n non nul, on a

$$p_{n}=0.75+0.25\times 0.2^{n+1}$$

 

7. Déterminer la limite de la suite $\left(p_{n}\right)$ et interpréter le résultat dans le contexte de l'exercice.

Cet exercice est un questionnaire à choix multiple.

 

Pour chaque question, une seule des quatre réponses proposées est exacte.

 

Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.

 

Aucune justification n'est demandée.

 

Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.

 

Les cinq questions sont indépendantes.

 

Dans tout l'exercice, $\mathbb{R}$ désigne l'ensemble des nombres réels.

 

1. Une primitive de la fonction $f$ , définie sur $\mathbb{R}$ par $(f)=xe^{x}$, est la fonction $F$, définie sur $\mathbb{R}$, par :

 

a. $f(x)=\dfrac{x^{2}}{2}\mathrm{e}^{x}$

 

b. $f(x)=(x-1)\mathrm{e}^{x}$

 

c. $f(x)=(x+1)\mathrm{e}^{x}$

 

d. $f(x)=x^{2}\mathrm{e}^{x^{2}}$

 

2. On considère la fonction $g$ définie par $g(x)=\ln\left(\dfrac{x-1}{2x+4}\right)$

 

la fonction $g$ est définie sur :

 

a. $\mathbb{R}$

 

b. $|-2\ ;\ +\infty|$

 

c. $|-\infty\ ;\ -2[\cup]1\ ;\ +\infty[$

 

d. $]-2\ ;\ 1[$

 

3; La fonction $h$ définie sur $\mathbb{R}$ par $h(x)=(x+1)\mathrm{e}^{x}$ est : 

 

a. concave sur $\mathbb{R}$

 

b. convexe sur $\mathbb{R}$

 

c. convexe sur $]-\infty\ ;\ -3]$ et concave sur $|-3\ ;\ 1[$

 

d. concave sur $]-\infty\ ;\ -3]$ et convexe sur $[-3\ ;\ +\infty[$

 

Une suite $\left(u_{n}\right)$ est minorée par $3$ et converge vers un réel $\ell$ 

 

On peut affirmer que :

 

a. $\ell=3$

 

b. $\ell\geq 3$

 

c. la suite $\left(u_{n}\right)$ est décroissante.

 

d. La suite $\left(u_{n}\right)$ est constante à partir d'un certain rang.

 

5. La Suite $\left(w_{n}\right)$ est définie par $w_{1}=2$ et pour tout entier naturel $n$ strictement positif,

 

$w_{n+1}=\dfrac{1}{n}w_{n}.$

 

a. La suite $\left(w_{n}\right)$ est géométrique

 

b. La suite $\left(w_{n}\right)$ n'admet pas de limite

 

c. $w_{5}=\dfrac{1}{15}$

 

d. La suite $\left(w_{n}\right)$ converge vers $0.$

Dans l'espace muni d'un repère orthonormé $\left(O\ ;\ \vec{i}\;,\vec{j}\;,\vec{k}\right)$ on considère les points

$$A(-1\ ;\ -3\ ;\ 2);,B(3\ ;\ -2\ ;\ 6)\text{ et }C(1\ ;\ 2\ ;\ -4)$$

 

1. Démontrer que les points $A$, $B$ et $C$ définissent un plan que l'on notera $\mathbb{P}.$

 

2.a. Montrer que le vecteur $\vec{n}\begin{pmatrix}13\\-16\\-9\end{pmatrix}$ est normal du plan $\mathbb{P}$

 

b. Démontrer qu'une équation cartésienne du plan $P$ est $13x-16y-9z-17=0$

 

On note $\mathcal{D}$ la droite passant par le point $F(15\ ;\ -16\ ;\ -8)$ et orthogonale au plan $\mathbbP}.$

 

3. Donner une représentation paramétrique de la droite $\mathcal{D}$

 

4. On appelle $E$ le point d'intersection de la droite D$\mathcal{D}$ et du plan $\mathbb{P}.$

 

Démontrer que le point $E$ a pour coordonnées $(2\ ;\ 0\ ;\ 1).$

 

5. Déterminer la valeur exacte de la distance du point $F$ au plan $\mathfrak{P}$

 

6. Déterminer les coordonnées du ou des point(s) de la droite $\mathcal{D}$ dont la distance au plan $\mathcal{P}$ est égale à la moitié de la distance du point $F$ au plan $\mathbb{P}.$