Bac Maths, S Pondichéry 26 avril 2017
Exercice 1 5 points
Les parties $A$, $B$ et $C$ peuvent être traitées de façon indépendante.
Dans tout l'exercice, les résultats seront arrondis, si nécessaire, au millième.
La chocolaterie « Choc'o » fabrique des tablettes de chocolat noir, de $100$ grammes, dont la teneur en cacao annoncée est de $85\%.$
$\textbf{Partie A}$
À l'issue de la fabrication, la chocolaterie considère que certaines tablettes ne sont pas commercialisables : tablettes cassées, mal emballées, mal calibrées, etc.
La chocolaterie dispose de deux chaînes de fabrication:
$\bullet\ $ la chaîne $A$, lente, pour laquelle la probabilité qu'une tablette de chocolat soit commercialisable est égale à $0.98.$
$\bullet\ $ La chaîne $B$, rapide, pour laquelle la probabilité qu'une tablette de chocolat soit commercialisable est $0.95.$
À la fin d'une journée de fabrication, on prélève au hasard une tablette et on note :
$A$ l' évènement: « la tablette de chocolat provient de la chaîne de fabrication $A$ » ;
$C$ l'évènement : « la tablette de chocolat est commercialisable ».
On note $x$ la probabilité qu'une tablette de chocolat provienne de la chaîne $A.$
- Montrer que $P(C)=0.03x+0.95$.
- À l'issue de la production, on constate que $96\%$ des tablettes sont commercialisables et on retient cette valeur pour modéliser la probabilité qu'une tablette soit commercialisable.
$\textbf{Partie B}$
Une machine électronique mesure la teneur en cacao d'une tablette de chocolat. Sa durée de vie, en années, peut être modélisée par une variable aléatoire $Z$ suivant une loi exponentielle de paramètre $\lambda$.
- La durée de vie moyenne de ce type de machine est de $5$ ans.
- Calculer $P(Z> 2)$.
- Sachant que la machine de l'atelier a déjà fonctionné pendant $3$ ans, quelle est la probabilité que sa durée de vie dépasse $5$ ans ?
$\textbf{Partie C}$
On note $X$ la variable aléatoire donnant la teneur en cacao, exprimée en pourcentage, d'une tablette de $100~g$ de chocolat commercialisable. On admet que $X$ suit la loi normale d'espérance $\mu = 85$ et d'écart type $\sigma = 2$.
- Calculer $P(83 < X < 87)$.
- Déterminer une valeur approchée au centième du réel $a$ tel que:
Interpréter le résultat dans le contexte de l'exercice.
- La chocolaterie vend un lot de \np{10000} tablettes de chocolat à une enseigne de la grande distribution. Elle affirme au responsable achat de l'enseigne que, dans ce lot, $90\%$ des tablettes ont un pourcentage de cacao appartenant à l'intervalle [81,7~;~88,3].
Au vu de l'échantillon prélevé, que peut-on conclure quant à l'affirmation de la chocolaterie ?
Exercice 2 3 points
On munit le plan complexe d'un repère orthonormé direct $(O,\ \vec{u},\ \vec{v})$.
- On considère l'équation
où $c$ est un réel strictement supérieur à $9.$
- Justifier que $(E)$ admet deux solutions complexes non réelles.
- Justifier que les solutions de $(E)$ sont $z_{\text{A}}=3+\text{i}\sqrt{c - 9}$ et $z_{\text{B}} =3-\text{i}\sqrt{c - 9}$.
- On note $A$ et $B$ les points d'affixes respectives $z_{\text{A}}$ et $z_{\text{B}}$.
- Démontrer qu'il existe une valeur du réel $c$ pour laquelle le triangle $OAB$ est rectangle et déterminer cette valeur.
Exercice 3 4 points
$\textbf{Commun à tous les candidats}$
Une entreprise spécialisée dans les travaux de construction a été mandatée pour percer un tunnel à flanc de montagne.
Après étude géologique, l'entreprise représente dans le plan la situation de la façon suivante : dans un repère orthonormal, d'unité $2~m$, la zone de creusement est la surface délimitée par l'axe des abscisses et la courbe $\mathcal{C}$.
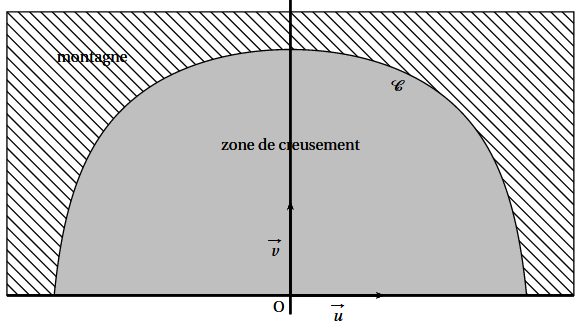
On admet que $\mathcal{C}$ est la courbe représentative de la fonction $f$ définie sur l'intervalle $[- 2,5~;~2,5]$ par:
$[f(x) = \ln \left(- 2x^2 + 13,5\right).]$
L'objectif est de déterminer une valeur approchée, au mètre carré près, de l'aire de la zone de creusement.
$\textbf{Partie A : Étude de la fonction}$ $f$
- Calculer $f'(x)$ pour $x \in [- 2,5~;~2,5]$.
- Dresser, en justifiant, le tableau de variation de la fonction $f$ sur $[- 2,5~;~2,5]$.
$\textbf{Partie B : Aire de la zone de creusement}$
On admet que la courbe $\mathcal{C}$ est symétrique par rapport à l'axe des ordonnées du repère.
- La courbe $\mathcal{C}$ est-elle un arc de cercle de centre $O$ ?
- Justifier la réponse.
- Justifier que l'aire, en mètre carré, de la zone de creusement est $\mathcal{A} = 8\displaystyle\int_0^{2,5} f(x)\:\text{d}x$.
- L'algorithme, donné en annexe, permet de calculer une valeur approchée par défaut de $I = \displaystyle\int_0^{2,5} f(x)\:\text{d}x$, notée $a$.
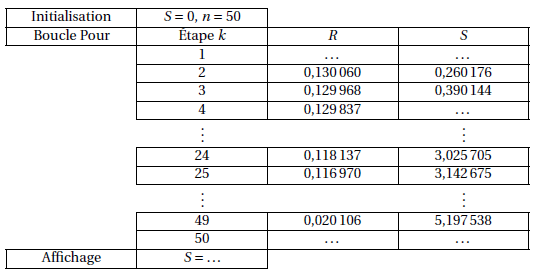
- Le tableau fourni en annexe, donne différentes valeurs obtenues pour $R$ et $S$ lors de l'exécution de l'algorithme pour $n = 50$.
- En déduire une valeur approchée, au mètre carré près, de l'aire de la zone de creusement.
Exercice 4 5 points
On considère deux suites $\left(u_n\right)$ et $\left(v_n\right)$ :
$\bullet~~$ la suite $\left(u_n\right)$ définie par $u_0 = 1$ et pour tout entier naturel
$n$ $u_{n+1} = 2u_n - n + 3$ ;
$\bullet~~$la suite $\left(v_n\right)$ définie, pour tout entier naturel $n$, par $v_n = 2^n$.
$\textbf{Partie A : Conjectures}$
Florent a calculé les premiers termes de ces deux suites à l'aide d'un tableur.
Une copie d'écran est donnée ci-dessous.
- Quelles formules ont été entrées dans les cellules $B3$ et $C3$ pour obtenir par copie vers le bas les termes des deux suites ?
- Pour les termes de rang $10$, $11$, $12$ et $13$ Florent obtient les résultats suivants :
Conjecturer les limites des suites $\left(u_n\right)$ et $\left(\dfrac{u_n}{v_n} \right)$.
$\textbf{Partie B : Étude de la suite } \left(u_n\right)$
- Démontrer par récurrence que, pour tout entier naturel $n$, on a
- Déterminer la limite de la suite $\left(u_n\right)$.
- Déterminer le rang du premier terme de la suite supérieur à $1$ million.
- Démontrer que la suite $\left(\dfrac{u_n}{v_n} \right)$ est décroissante à partir du rang $3.$
- On admet que, pour tout entier $n$ supérieur ou égal à $4$, on a : $0 < \dfrac{n}{2^n} \leqslant \dfrac{1}{n}$.
Exercice 4 5 points
On définit les suites $\left(u_n\right)$ et $\left(v_n\right)$ par :
\[u_0 = v_0 = 1\: \text{et, pour tout entier naturel }\:n,\: u_{n+1} = 2u_n + 3v_n\: \text{et}\: v_{n+1} = 2u_n + v_n.\]
On admettra que les termes de ces suites sont des entiers naturels non nuls.
$\textbf{Partie A : Conjectures}$
Flore a calculé les premiers termes des suites à l'aide d'un tableur.
Une copie d'écran est donnée ci-dessous.
- Quelles formules ont été entrées dans les cellules B3 et C3 pour obtenir par copie vers le
- Soit $n$ un entier naturel.
- Pour les termes de rang $10$, $11$, $12$ et $13$ Flore obtient les résultats suivants :
Elle émet la conjecture : « la suite $\left(\dfrac{u_n}{v_n} \right)$ converge ».
Qu'en penser ?
$\textbf{Partie B : Étude arithmétique}$
- Démontrer par récurrence que, pour tout entier naturel $n$, on a :
- Soit $n$ un entier naturel.
$\textbf{Partie C : Étude matricielle}$
Pour tout entier naturel $n$, on définit :
$\bullet\ $ la matrice colonne $X_n = \begin{pmatrix}u_n\\ v_n\end{pmatrix}$,
$\bullet\ $ les matrices carrées $P = \begin{pmatrix} 1&3\\- 1&2\end{pmatrix}$ et $Q_n = \begin{pmatrix}(- 1)^n&3 \times 2^{2n}\\(- 1)^{n+1}&2^{2n+1}\end{pmatrix}.$
1. a. Montrer que la matrice $\dfrac{1}{5}\begin{pmatrix}2&- 3\\1&1\end{pmatrix}$ est l'inverse de $P$.
Démontrer que, pour tout entier naturel $n$, on a
$\left\{\begin{array}{l c l}
u_n&=&\dfrac{(- 1)^{n+1}+ 3\times 2^{2n+1}}{5}\\
v_n&=&\dfrac{(- 1)^{n}+ 2^{2n+2}}{5}
\end{array}\right.$
- a. Vérifier que, pour tout entier naturel $n$, on a $\dfrac{u_n}{v_n}= \dfrac{\frac{(- 1)^{n+1}}{2^{2n+1}}+ 3}{\frac{(- 1)^{n}}{2^{2n+1}}+ 2}$.
Exercice 5 3 points
$\textbf{Commun à tous les candidats}$
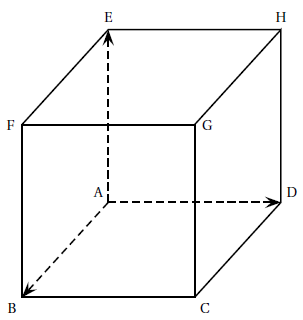
On considère un cube $ABCDEFGH$ fourni en annexe.
L'espace est rapporté au repère $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
On note $\mathcal{P}$ le plan d'équation $x + \dfrac{1}{2} y +\dfrac{1}{3}z -1 = 0$.
Construire, sur la figure fournie en annexe, la section du cube par le plan $\mathcal{P}$.
La construction devra être justifiée par des calculs ou des arguments géométriques.
Exercice 3
Le tableau ci-dessous donne les valeurs de $R$ et de $S$, arrondies à $10^{-6}$, obtenues lors de l'exécution de l'algorithme pour $n = 50$.
Exercice 5

Ajouter un commentaire