Bac Maths S2 2e groupe 2015

La figure ci-dessous est la représentation graphique d'une fonction $f.$

 

 

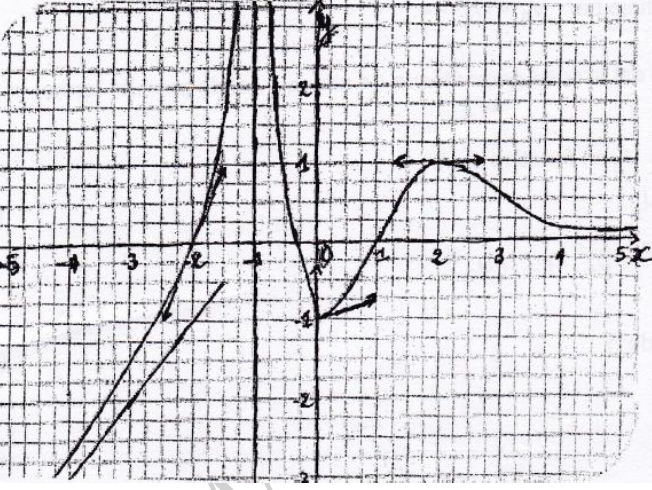
1) a) Déterminer l'ensemble de définition de la fonction $f.$

 

b) Déterminer les limites suivantes :

 

$\lim_{x\rightarrow -\infty}f(x)\;,\quad \lim_{x\rightarrow +\infty}f(x)\;,\quad \lim_{x\rightarrow -1}f(x)\;,\quad \lim_{x\rightarrow +\infty}\dfrac{x}{f(x)}$ 

 

$\lim_{x\rightarrow -\infty}f\left(\dfrac{3}{x^{2}}\right)\;,\quad \lim_{x\rightarrow 0^{-}}\dfrac{f(x)+1}{x}$

 

c) Préciser la nature de chacune des branches infinies au voisinage de $+\infty$ et au voisinage de $-\infty.$

 

d) Résoudre graphiquement l'équation $f(x)=0.$

 

2) Déterminer $f'(-2)\;;\ f'(2)\;;\ f'_{d}(0).$

 

3) Dresser le tableau de variation de la fonction $f.$

Soit $(U_{n})$ la suite définie par : $\left\lbrace\begin{array}{rcl} U_{0} &=& 0\\ \\ U_{n+1} &=& \dfrac{1}{2}\sqrt{U_{n}^{2}+12}\end{array}\right.$

 

1) Calculer $U_{1}$ et $U_{2}.$

 

2) Soit $(V_{n})$ la suite définie par : $V_{n}=U_{n}^{2}-4$

 

a) Montrer que $(V_{n})$ est la suite géométrique de raison $\dfrac{1}{4}$ et de premier terme -4.

 

b) Exprimer $V_{n}$ puis $U_{n}$ en fonction de $n.$

 

Calculer $\lim_{n\rightarrow +\infty}U_{n}$

 

3) On pose $S_{n}=U_{0}^{2}+U_{1}^{2}+\cdots+U_{n}^{2}.$

 

Exprimer $S_{n}$ en fonction de $n.$

 

Calculer $\lim_{n\rightarrow +\infty}\dfrac{S_{n}}{n}$

Un automobiliste rencontre sur son trajet quotidien, et successivement, sept feux de croisement, chacun pouvant être en l'état R (rouge), V (vert), O (orange).

 

Nous appellerons "parcours" la suite des sept feux dans l'état où l'automobiliste les rencontre, Ainsi (R, V, O, R, V, O, R) représentera un de ces parcours.

 

1) Quel est le nombre de parcours possibles ?

 

2) Quel est le nombre de parcours qui correspondent aux conditions suivantes :

 

a) "Tous les feux sauf le premier sont au rouge"

 

b) "Le premier des feux est au vert" ;

 

c) "Tous les feux sauf un sont au rouge"

 

d) "L'automobiliste s'arrête au moins cinq fois (il est convenu que l'automobiliste s'arrête lorsque le feu est au rouge ou à l'orange)"

Soit $Z=(1+\mathrm{i})^{2015}+(1-\mathrm{i})^{2015}$  où $\mathrm{i}^{2}=-1.$

 

1) Montrer que $Z$ est un réel sans le calculer.

 

2) Écrire sous forme exponentielle $(1+\mathrm{i})^{2015}$ et $(1-\mathrm{i})^{2015}.$

 

En déduire la valeur de $Z.$