Bac Physique Chimie 1er Groupe S1 S3 2013

On réalise la décomposition catalytique du péroxyde d'hydrogène (eau oxygénée) de formule $H_{2}O_{2}$ dans un ballon maintenu à température constante.

 

A un instant pris comme origine des dates, on verse dans le ballon contenant déjà le catalyseur, une quantité d'eau oxygénée nécessaire pour que la solution ait un volume de $1\;L$ et une concentration $C_{0}$ de $5\cdot10^{-2} mol\cdot L^{-1}$ en eau oxygénée. 

 

La mesure du volume de dioxygène dégagé a permis de déterminer la concentration molaire volumique $C$ en eau oxygénée. 

 

Cette concentration varie en fonction du temps dans l'intervalle $[0\;,\ 6\;h]$ selon la loi suivante : 

 

$C=C_{0}\,\mathrm{e^{-kt}}\text{ avec }k=0.464\;h^{-1}.$

 

1.1 Écrire l'équation-bilan de la réaction de décomposition de l'eau oxygénée. 

 

Potentiels normaux des couples : 

 

$O_{2}/H_{2}O_{2}(0.68V)\;;\ H_{2}O_{2}/H_{2}O(1.77V)$ $(0.25\;point)$

 

1.2 Tracer la courbe représentant la concentration $C$ en fonction du temps $C=f(t)$ dans l'intervalle de temps $[0\;,\ 6\;h].$ $(0.5\;point)$

 

1.3 Donner l'expression de la vitesse $v$ de disparition de l'eau oxygénée en fonction du temps dans l'intervalle $[0\;,\ 6\;h].$

 

Calculer $v$ pour $t=3\;h.$ $(0.75\;point)$

 

1.4 Retrouver la valeur de $v$ calculée précédemment pour $t=3\;h$ par une méthode graphique. $(0.5\;point)$

 

1.5 Définir le temps de demi-réaction sachant que la réaction est totale. 

 

Déterminer graphiquement puis par calcul sa valeur. $(01\;point)$

2.1 L'acide méthanoïque a pour formule semi-développé $HCO_{2}H$ et pour masse molaire moléculaire $M\left(HCO_{2}H\right)=46.0\;g\cdot mol^{-1}.$

 

Dans ce qui suit, la solution commerciale $S_{0}$ d'acide méthanoïque utilisée a une masse volumique $\rho=1.15\;kg\cdot L^{-1}$ et contient en masse $80.0\%$ d'acide méthanoïque pur.

 

2.1.1 Montrer que la concentration $C_{0}$ de la solution commerciale $S_{0}$ est de l'ordre de $20\;mol\cdot L^{-1}$ $(0.25\;point)$

 

2.1.2 Un professeur propose, en $TP$, à un groupe d'élèves de préparer un volume. 

 

$V=1.00\;L$ d'une solution $S$ d'acide méthanoïque de concentration $C=5.00\cdot10^{-2} mol\cdot L^{-1}.$

 

2.1.2.1 Déterminer le volume $V_{0}$ de la solution commerciale à prélever pour préparer la solution $S.$ $(0.25\;point)$

 

2.1.2.2 Décrire le protocole expérimental de préparation de la solution $S$ $(0.5\;point)$

 

2.1.2.3 La mesure du $pH$ de la solution $S$ obtenue montre que la concentration des ions hydronium est $\left[H_{3}O^{+}\right]=2.50\cdot10^{-2} mol\cdot L^{-1}.$ 

 

Montrer que l'acide méthanoïque réagit partiellement avec l'eau. $(0.25\;point)$

 

2.2 Pour réaliser le dosage de $10\;mL$ de la solution $S$, on dispose au laboratoire de solutions aqueuses de soude (ou d'hydroxyde de sodium).

 

2.2.1 Écrire l'équation chimique de la réaction support du dosage de l'acide méthanoïque par la soude. $(0.25\;point)$

 

2.2.2 Calculer la constante de réaction $K$ pour cette réaction support du dosage. Pourrait-on en déduire que cette réaction peut être utilisée pour doser l'acide ? $(0.5\;point)$

 

2.2.3. Définir l'équivalence acido-basique. $(0.5\;point)$

 

2.2.4. Pour réaliser le dosage le groupe d'élèves dispose sur la paillasse de deux solutions aqueuses de soude $S_{1}$ et $S_{2}$ de concentrations molaires respective : 

 

$C_{1}=2.00\cdot10^{-1} mol\cdot L^{-1}$ et : 

 

$C_{2}=2.5\cdot10^{-2} mol\cdot L^{-1}.$ 

 

Quelle est parmi les deux solutions de soude proposées, celle qui semble la plus adaptée au dosage ? 

 

Justifier votre réponse. $(0.5\;point)$

 

Données : 

 

$pKe=14.0$ :   $pKa\left(HCO_{2}H/HCO_{2}^{-}\right)=3.8.$

Le cobalt $^{60}_{27}Co$ radioélément très utilisé en médecine pour le traitement du cancer (« bombe au cobalt ») est obtenu par bombardement neutronique du cobalt « naturel » $_{27}^{59}Co.$

 

3.1 Écrire l'équation de production du cobalt $^{60}_{27}Co$ $(0.25\;point)$

 

3.2 Le cobalt $_{27}^{60}Co$ est radioactif $\beta^{-}$ et a une constante radioactive $\lambda=4\cdot10^{-9}s^{-1}.$

 

Écrire l'équation de la réaction de désintégration de $^{60}_{27}Co$  $(0.5\;point)$

 

Extrait de la classification périodique :

$$\begin{array}{|c|c|c|c|c|} \hline _{25}Mn&_{26}Fe&_{27}Co&_{28}Ni&_{29}Cu\\ \hline \end{array}$$

 

3.3 Le noyau fils $Y$ est obtenu à l'état excité d'énergie $E_{3}=2.50MeV.$ 

 

Sa désexcitation s'effectue en deux étapes comme indiqué ci-dessous :

 

 

 

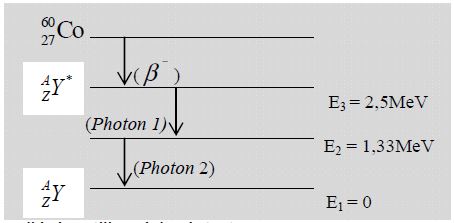
Calculer les longueurs d'onde $\lambda_{1}$ et $\lambda_{2}$ des deux photons émis au cours de la désexcitation du noyau fils $Y.$ $(0.5\;point)$

 

3.4 Un centre hospitalier dispose d'un échantillon de « cobalt $60$ » de masse $m_{0}=1\mu g$

 

3.4.1. Déterminer le nombre de noyau $N_{0}$ contenus dans l'échantillon à la date $t=0.$ $(0.25\;point)$

 

3.4.2. Soit $N(t)$ le nombre de noyaux présents dans l'échantillon à la date $t.$

 

Établir la relation $N(t)=N_{0}\mathrm{e}^{-\lambda t}.$ $(0.25\;point)$

 

3.4.3 Le technicien du laboratoire est chargé de contrôler cette source, tous les ans, en déterminant son activité.

 

3.4.3.1 Définir l'activité $A(t)$ d'une substance radioactive puis l'exprimer en fonction de $A_{0}$

 

(activité à $t=0$), $\lambda$ et $t.$ $(0.5\;point)$

 

3.4.3.2 Le technicien obtient les résultats suivants :

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline t\text{(ans)}&0&1&2&3&4&5&7\\ \hline A\left(10^{7}Bq\right)&3.980&3.515&3.102&2.670&2.368&2.038&1.540\\ \hline In\;A& & & & & & &\\ \hline \end{array}$$

 

a) Recopier puis compléter le tableau et tracer le graphe $ln\;A=f(t).$ $(0.75\;point)$

 

b) En déduire la constante radioactive $\lambda$ du « cobalt $60$ ». $(0.5\;point)$

 

On donne : 

 

Constante d'Avogadro $N_{A}=6.02\cdot10^{23}mol^{-1}$ ; 

 

$M\left(^{60}_{27}Co\right)=60\;g\cdot mol^{-1}$

 

Célérité de la lumière $C=3.00\cdot10^{8}m\cdot s^{-1}$ ; 

 

Constante de Planck : $h=6.62\cdot10^{-34} J\cdot s$

Pour créer un champ magnétique uniforme on utilise les bobines de Helmholtz. 

 

Ce sont deux bobines plates identiques, coaxiales, séparées par une distance égale à leur rayon $R$ et parcourues par des courants de même intensité $I$ et de même sens. 

 

Dans l'espace entre les bobines règne un champ magnétique uniforme horizontal $\overrightarrow{B}$ (figures a et b)

 

 

 

 

 

 

 

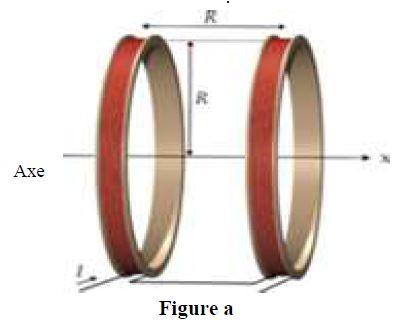
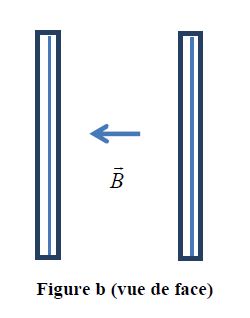
4.1 Sur la figure b est représenté le vecteur champ magnétique $\overrightarrow{B}$ créé par les bobines. 

 

Recopier cette figure, indiquer le sens des courants dans les bobines et représenter trois lignes de champ. $(0.5\;point)$

 

4.2 Pour étudier le mouvement d'une particule chargée dans $\overrightarrow{B}$, on place entre les deux bobines une ampoule contenant un canon à électrons. 

 

En faisant pivoter l'ampoule on peut donner une orientation au vecteur vitesse $\overrightarrow{v_{0}}$ des électrons sortant du canon. 

 

On négligera dans la suite le poids de l'électron.

 

4.2.1 Donner l'expression vectorielle de la force subie par un électron animé d'une vitesse $\overrightarrow{v_{0}}$ dans le champ magnétique. $(0.25\;point)$

 

4.2.2 L'ampoule est orientée de sorte que la vitesse $\overrightarrow{v_{0}}$ des électrons soit parallèle à $\overrightarrow{B}.$

 

Déterminer la nature du mouvement de ces électrons. 

 

Justifier. $(0.25\;point)$

 

4.2.3 L'ampoule est maintenant orientée de sorte que $\overrightarrow{v_{0}}$ soit orthogonale à $\overrightarrow{B}.$

Déterminer dans ce cas la nature du mouvement des électrons. $(0.75\;point)$

 

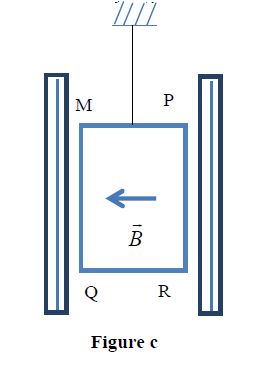
4.3 On place maintenant entre les deux bobines de Helmholtz une bobine plate rectangulaire de cotés $MP=QR=a=4\;cm$ et $MQ=PR=b=6\;cm$ comportant $N=40$ tours de fil conducteur. 

 

Elle est suspendue par un fil de constante de torsion $C$, vertical, passant par le milieu de $MP$ (figure c).

 

La bobine plate est en équilibre de telle sorte que $\overrightarrow{B}$ soit parallèle aux cotés horizontaux.

 

On fait passer dans la bobine plate un courant d'intensité constante $I'=0.5\;A.$

 

4.3.1 Préciser la nature et le nom des forces exercées par le champ magnétique sur les côtés de la bobine. 

 

Donner les caractéristiques de la force agissant sur chaque côté en faisant un schéma clair où figureront les sens du courant $I'$, de $\overrightarrow{B}$ et de la force éventuellement. $(01\;point).$

 

On prendra $\overrightarrow{B}=4\cdot10^{-2}T.$

 

4.3.2 La bobine plate quittera-t-elle sa position d'équilibre initiale ? 

 

Justifier. $(0.25\;point).$

 

4.3.3 Sachant que la bobine plate tourne d'un angle de $\dfrac{\pi}{6}$ rad et s'immobilise à nouveau, exprimer la somme des moments des forces par rapport à l'axe du fil de suspension.

 

En déduire la constante de torsion $C$ du fil. $(0.75\;point)$

 

4.4 La bobine plate est en équilibre et placée de telle sorte son plan soit orthogonal au vecteur champ magnétique $\overrightarrow{B}$ ; on y fait passer un courant d'intensité $I'=0.5A.$

 

4.4.1 Donner les caractéristiques de la force agissant sur chaque côté en faisant un schéma clair où figureront les sens du courant $I'$, de $\overrightarrow{B}$ et de la force. $(01\;point).$

 

4.4.2 La bobine quittera-t-elle sa position d'équilibre ? 

 

Justifier la réponse. $(0.5\;point).$

On réalise le circuit de la figure (1) comprenant :

 

-un générateur de tension continue de f.e.m $E=4.5V$

 

-un condensateur de capacité $C$,

 

-une bobine d'inductance $L$ et de résistance négligeable,

 

-un conducteur ohmique de résistance $R=1000\Omega$,

 

-un conducteur ohmique de résistance $R'$ variable.

 

 

 

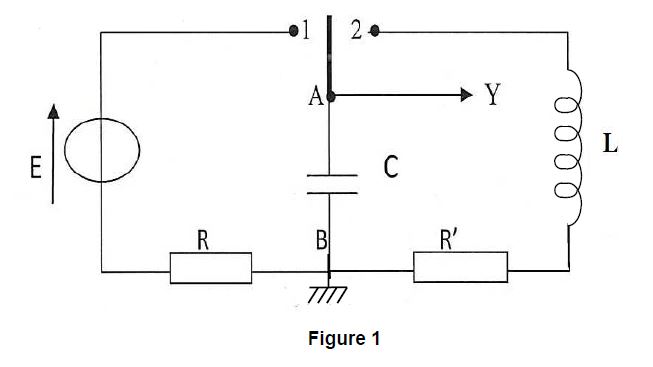
Un oscillographe permet de visualiser la tension aux bornes du condensateur.

 

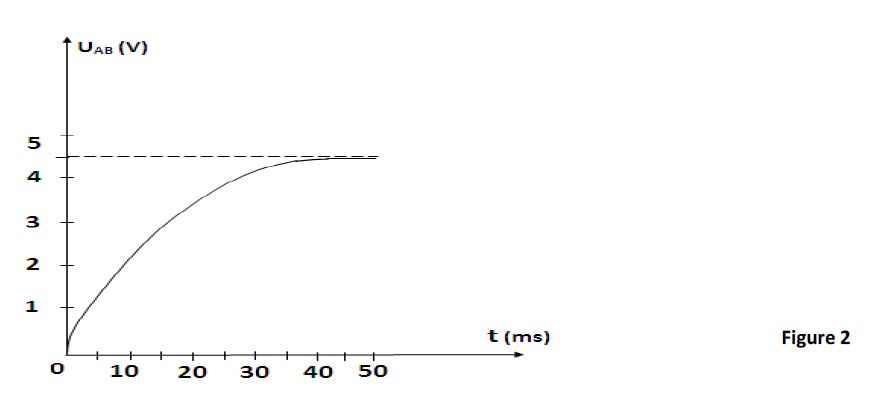
5.1 On ferme l'interrupteur $K$ en position $1.$ L'oscillogramme visualisé sur l'écran de l'oscillographe est reproduit sur la figure (2)

 

 

 

5.1.1 Que se passe-t-il pour le condensateur ? $(0.25\;point)$

 

5.1.2 Montrer que la tension $u_{AB}$ aux bornes du condensateur, notée $u$, vérifie l'équation différentielle :

 

$\dfrac{\mathrm{d}u}{\mathrm{d}t}+a\,u=b$ , équation où $a$ et $b$ sont des constantes à déterminer. $(0.5\;point)$

 

5.1.3 Exprimer la constante de temps $\mathfrak{t}$ du circuit en fonction des données et donner sa signification physique. $(0.5\;point)$

 

5.1.4 Déterminer graphiquement $\mathfrak{t}$ et en déduire la capacité $C$ du condensateur. $(0.5\;point)$

 

5.2 On ferme l'interrupteur en position $2$ après avoir annulé la valeur de $R'$ à la date $t=0.$

 

5.2.1. Écrire l'équation différentielle vérifiée par la charge $q$ du condensateur. $(0.25\;point)$

 

5.2.2 En déduire l'équation différentielle vérifiée par la tension $u.$ $(0.25\;point)$

 

5.2.3 On admet que la solution de l'équation différentielle est de la forme : 

 

$u(t)=D\cos Ft$, expression où $D$ et $F$ sont des constantes. 

 

Déterminer $D$ et $F$ en fonction des caractéristiques des dipôles du montage. $(0.5\;point)$

 

5.2.4 Calculer l'énergie maximale emmagasinée par le condensateur. $(0.25\;point)$

 

5.3 L'interrupteur toujours fermé en position $2$, on réalise les trois expériences ci-dessous en faisant varier les valeurs de la résistance $R'$ et de l'inductance $L.$

$$\begin{array}{|c|c|c|c|} \hline \text{Expériences}&R'(\Omega)&L(H)&C(\mu F)\\ \hline E_{1}&100&1.0&5\\ \hline E_{2}&50&0.2&5\\ \hline E_{3}&50&1.0&5\\ \hline \end{array}$$

 

Les oscillogrammes obtenus ont été reproduits sur les figures (3), (4) et (5). 

 

 

 

 

 

 

 

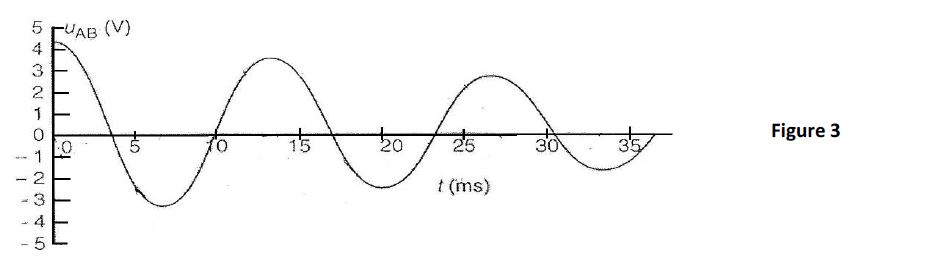
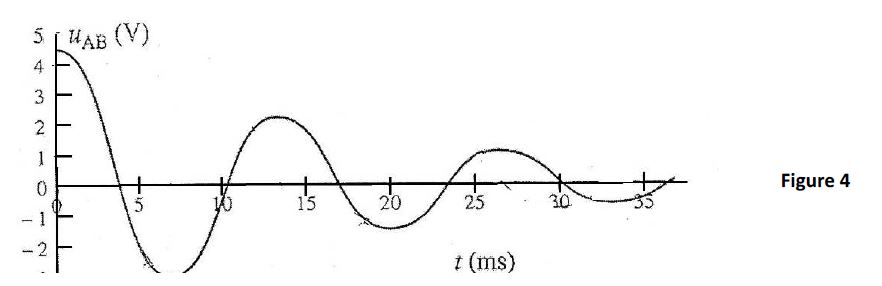
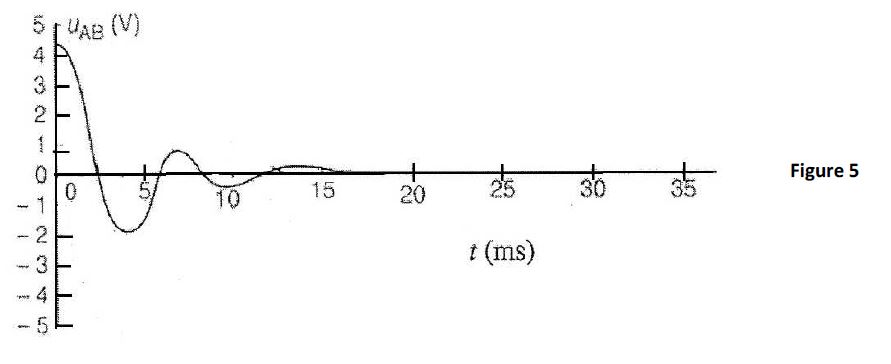
On admet que l'amortissement ne modifie pas sensiblement la fréquence des oscillations...

 

5.3.1 Calculer pour chaque expérience la période propre des oscillations. $(0.5\;point)$

 

5.3.2 Déterminer les valeurs des périodes à partir des figures (3), (4) et (5). $(0.5\;point)$

 

5.3.3 Faire correspondre chaque figure à une des trois expériences en justifiant. $(0.5\;point)$

 

5.3.4 Calculer dans chaque expérience l'énergie dissipée par effet joule lors de la première oscillation. $(0.75\;point)$