Bac Physique Chimie 1er Groupe S1 S3 2016

L'aspirine est bien connue pour ses propriétés analgésiques (diminution de la douleur et de la fièvre) et anticoagulantes. 

 

Sa formule développée est :

 

 

 

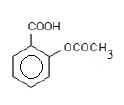
1.1 L'aspirine peut être synthétisée en faisant réagir l'anhydride éthanoïque et l'acide $2$-hygroxybenzoïque (également appelé acide salicylique).

 

1.1.1 Écrire les formules semi-développées de l'anhydride éthanoïque et de l'acide salicylique. $(0.5\;point)$

 

1.1.2 Écrire l'équation bilan de la réaction de synthèse de l'aspirine. $(0.5\;point)$

 

1.1.3 Donner le nom de cette réaction et rappeler ses caractéristiques.  $(0.5\;point)$

 

1.2 Pour réaliser une synthèse de l'aspirine, on introduit dans un erlenmeyer bien sec $3.0\;g$ d'acide salicylique et $7.0\;mL$ d'anhydride éthanoïque et quelques gouttes d'acide sulfurique concentré.

 

Le mélange est correctement chauffé au bain-marie durant quelques minutes.

 

1.2.1 Montrer que l'un des réactifs est en excès. $(0.5\;point)$

 

1.2.2 Après cristallisation et filtration, on obtient une masse d'aspirine $m=3.8\;g.$

 

Calculer le rendement de cette réaction de synthèse et commenter le résultat en rapport avec la prévision théorique. $(0.5\;point)$

 

1.2.3 Écrire l'équation de la réaction parasite qui se produirait si l'erlenmeyer n'était pas bien sec. $(0.5\;point)$

 

On donne :

$$\begin{array}{|c|c|c|} \hline \text{Acide salicylique}&138\;g\cdot mol^{-1}&\text{densité}=1.44\\ \hline \text{Anhydride éthanoïque}&102\;g\cdot mol^{-1}&\text{densité}=1.08\\ \hline \text{Acide acétylsalicylique}&150\;g\cdot mol^{-1}&\text{densité}=1.40\\ \hline \end{array}$$

Données : 

 

masses molaires en $g\;mol^{-1}$ $M(C)=12$ ; $M(O)=16$ $M(H)=1.$

 

2.1 La solucitrine est un médicament indiqué pour le traitement des maux de gorge. 

 

Ce médicament contient de l'acide ascorbique de formule brute $C_{6}H_{8}O_{6}.$

 

On prépare une solution $S_{0}$ en dissolvant un comprimé de « solucitrine $500$ » dans $100\;mL$ d'eau distillée. 

 

On prélève $20\;mL$ de cette solution $S_{0}$ que l'on dose par une solution d'hydroxyde de sodium de concentration $C_{b}=5.0\cdot10^{-2} mol\cdot L^{-1}.$ 

 

La mesure du $pH$ du milieu réactionnel a permis d'obtenir le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline V_{b}(mL)&2.5&3.0&3.5&4.0&4.5&5.0&5.5&6.0\\ \hline pH&3.63&3.74&3.83&3.92&4.01&4.10&4.19&4.28\\ \hline \left[H_{3}O^{+}\right]\left(mol\cdot L^{-1}\right)& & & & & & & &\\ \hline \dfrac{1}{V_{b}}\left(mL^{-1}\right)& & & & & & & &\\ \hline \end{array}$$

 

2.1.1 Écrire l'équation de la réaction qui a lieu entre l'acide ascorbique, noté $AH$, et la solution d'hydroxyde de sodium, au cours du dosage. $(0.25\;point)$

 

2.1.2 Définir l'équivalence acido-basique. $(0.25\;point)$

 

2.2 On note $n_{a}$ la quantité de matière d'acide restant dans le milieu réactionnel, $v_{bE}$ le volume de solution d'hydroxyde de sodium versé dans ce milieu réactionnel à l'équivalence.

 

2.2.1 Établir la relation $n_{a}=C_{b}(v_{bE}-v_{b}).$ $(0.25\;point)$

 

2.2.2 Vous aidant de la relation établie en (2.2.1) exprimer, en fonction de $v_{b}$ et $v_{bE}$ le rapport $\dfrac{[AH]}{[A^{-}]}$ $(0.5\;point)$

 

2.2.3 Exprimer ensuite la concentration $\left[H_{3}O^{+}\right]$ en fonction de $v_{b}$ , $v_{bE}$ et la constante d'acidité $Ka$ du couple $AH/A^{-}.$ $(0.25\;point)$

 

2.3 Exploitation du tableau de valeurs.

 

2.3.1 Recopier puis compléter le tableau de valeurs. $(0.25\;point)$

 

2.3.2 Tracer la courbe $\left[H_{3}O^{+}\right]=f\left(\dfrac{1}{V_{b}}\right)$ $(0.5\;point)$

 

2.3.3 Déterminer, graphiquement, le $pKa$ du couple $AH/A^{-}$ ainsi que le volume $V_{bE}.$ $(0.5\;point)$

 

2.4 calculer la masse d'acide ascorbique contenue dans un comprimé de solucitrine.

 

Justifier l'appellation « solucitrine $500$ ». $(0.25\;point)$

3.1 Deux ressorts identiques, de longueur à vide $L_{0}=10\;cm$, de raideur $k=20N\cdot m^{-1}$ sont tendus et fixés à deux supports $P_{1}$ et $P_{2}$, distants de $L=30\;cm$, sur un plan incliné d'un angle $\alpha=30^{\circ}$

 

Un solide ponctuel S de masse $m=100\;g$ est fixé aux deux ressorts (fig 1).

 

 

 

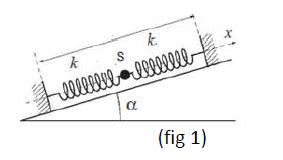
3.1.1 Recopier la figure, puis représenter les forces qui s'exercent sur le solide ponctuel $S$, à l'équilibre. $(0.25\;point)$

 

3.1.2 Calculer, le solide ponctuel $S$ étant en équilibre, les allongements respectifs des ressorts $(R_{1})$ et $(R_{2}).$ $(0.5\;point)$

 

3.2 On associe à cet ensemble un repère constitué d'un axe $(X'X)$ orienté vers le haut et parallèle à la direction des ressorts. 

 

L'origine de ce repère coïncide avec la position du solide $S$, au repos. 

 

A la date $t_{0}=0$, le solide $S$ est déplacé de sa position d'équilibre, le long de l'axe, vers le bas, de $2\;cm$, puis lâché sans vitesse initiale.

 

Le niveau de référence de l'énergie potentielle de pesanteur coïncide avec la position du solide $S$ en équilibre.

 

3.2.1 En négligeant l'action de l'air, établir à partir d'une étude dynamique, l'équation différentielle du mouvement du solide $S.$ $(0.5\;point)$

 

3.2.2 Préciser la nature du mouvement du solide $S$ ; exprimer ensuite la période propre, $T_{0}$, de ce mouvement. $(0.25\;point)$

 

3.2.3 Établir l'expression de l'énergie potentielle du système « ressorts, solide $S$ et terre ». $(0.5\;point)$

 

3.3 On néglige toujours les forces de frottement. 

 

On note $x$ la position du solide $S$ et $\dot{x}=\dfrac{\mathrm{d}x}{\mathrm{d}t}$ sa vitesse.

 

Montrer que ces deux paramètres d'évolution du solide $S$, la position et la vitesse, obéissent à une relation de la forme : 

 

$\dot{x}^{2}+A^{2}x-B^{2}=0$, où $A$ et $B$ sont des constantes positives dont on précisera les expressions. $(0.5\;point)$

 

3.4 Grâce à des capteurs on peut enregistrer l'évolution temporelle de la position $x$ du solide ponctuel $S$ puis tracer les courbes qui donnent son énergie cinétique $E_{c}$ et de l'énergie potentielle $E_{p}$ du système « ressort-solide $(S)$-terre » en fonction du temps.

 

 

 

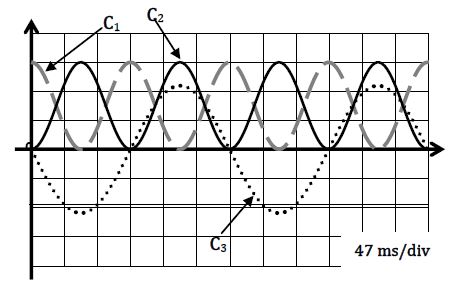
3.4.1 Identifier, en justifiant, la courbe relative à la vitesse du solide, celle relative à son énergie cinétique et celle relative à l'énergie potentielle du système « ressorts-solide $S$ et terre ». $(0.25\;point)$

 

3.4.2 Déterminer graphiquement les valeurs des périodes $T$ et $T_{0}$, respectives, de l'énergie potentielle $E_{p}$ et de la position instantanée $x$ du solide $S.$ 

 

Les comparer. $(0.5\;point)$

 

3.5 Déterminer, en millijoules, la valeur de chaque division de l'axe des énergies.

 

En déduire la vitesse maximale du solide $S.$ $(0.75\;point)$

Dans tout l'exercice les ions se déplacent dans le vide et leur poids est négligeable devant les autres forces. 

 

On cherche à identifier les isotopes de l'hydrogène.

 

4.1 Dans la chambre d'ionisation d'un spectrographe de masse, les atomes d'hydrogène sont transformés en ions $H^{+}.$ 

 

Chaque ion, de masse $m$ et de charge $q$, sort de la chambre d'ionisation avec une vitesse quasiment nulle et est accéléré entre deux plaques $P_{1}$ et $P_{2}$ par une tension $U=V_{P1}-V_{P2}$, de valeur réglable. 

 

Ces ions sont ensuite déviés entre $E$ et $S$ par un champ magnétique uniforme. 

 

Ils sont enfin recueillis à l'entrée fixe $C$ d'un collecteur à la sortie du champ magnétique (voir fig 2).

 

 

 

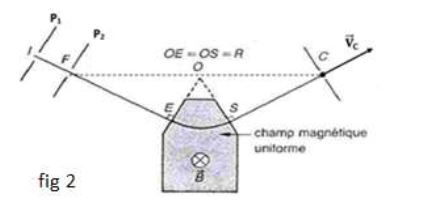
4.1.1 Établir en fonction de la charge $q$, de la masse $m$ de l'ion $H^{+}$ et de la tension $U$ l'expression de la vitesse $V$ avec laquelle un ion hydrogène pénètre en $E$ dans le domaine du champ magnétique. $(0.5\;point)$

 

4.1.2 Montrer que la portion $(E\;,\ S)$ de la trajectoire de chaque ion est un arc de cercle de centre $O$ et de rayon $R.$ 

 

On exprimera ce rayon $R$ en fonction de la charge $q$ , de la vitesse $V$ , de l'intensité $B$ du champ magnétique et de la masse $m$ puis en fonction de $q$, $B$ , de la tension $U$ et $m.$ $(0.5\;point)$

 

4.1.3 Établir l'expression de la durée $\mathcal{t}$ de la traversée de l'espace champ magnétique par les ions en fonction de $q$, $B$, $m$ et de l'angle $\beta=\text{angle}(\widehat{EOS})$ $(0.25\;point)$

 

4.2 La chambre d'ionisation contient un mélange d'isotopes de l'hydrogène.

 

Tous les ions que l'on veut recueillir dans le collecteur doivent suivre le même trajet $(IFESC).$

 

4.2.1 Pour que les ions $\left(^{1}_{1}H^{+}\right)$ soient collectés en $C$, il faut donner à la tension réglable, la valeur $U_{0}=8025V.$

 

Calculer le rayon de leur trajectoire dans le champ magnétique d'intensité $B=0.5T.$ $(0.25\;point)$

 

4.2.2 Pour recueillir les autres isotopes de l'hydrogène dans le collecteur en $C$ suivant le même trajet, il faut donner à la tension réglable, des valeurs comprises entre $U_{1}=2675V$ et $U_{2}=5350V.$

 

En déduire les valeurs des nombres de masse des autres isotopes de l'hydrogène. $(0.5\;point)$

 

4.3 Les points $F$, $O$ et $C$ se trouvent sur une même droite.

 

Établir la relation : $$D=\dfrac{4}{B}\sqrt{\dfrac{mU}{q\left(1-\cos\beta\right)}}\text{ avec }D=FC.\qquad(0.5\;point)$$

 

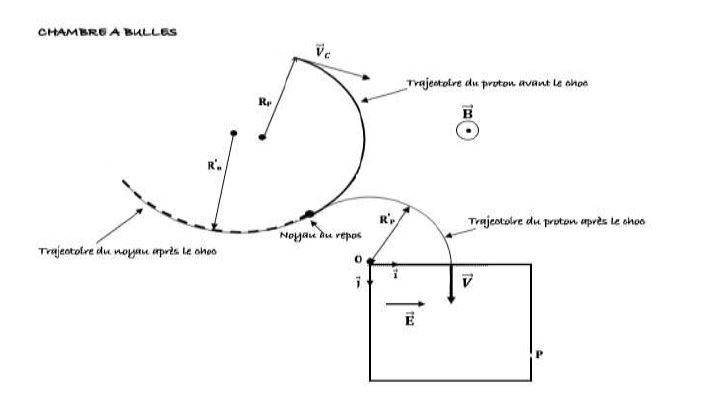
4.4 Sorti du collecteur, l'isotope $^{1}_{1}H^{+}$ qui est le proton, pénètre avec la vitesse $\overrightarrow{v_{c}}$ dans un domaine où règne un champ magnétique uniforme $\overrightarrow{B'}$, perpendiculaire à $\overrightarrow{v_{c}}$ (voir schéma en annexe).

 

4.4.1 Calculer le rayon $R'$ de sa trajectoire. 

 

On donne $B'=0.5T$ et $v_{c}=1.24\cdot10^{6}m\cdot s^{-1}.$ $(0.25\;point)$

 

4.4.2 En réalité, pendant qu'il est dans le domaine où règne le champ magnétique $\overrightarrow{B'}$, le proton heurte une autre particule, un noyau initialement au repos. 

 

Le choc qui en résulte est élastique. 

 

On considérera que les vitesses, juste avant et après le choc, sont colinéaires.

 

Exprimer les normes des vitesses respectives $v'_{p}$ et $v'_{n}$ du proton et du noyau après le choc en fonction de la masse $m_{p}$ du proton, de la masse $m_{n}$ du noyau et de la vitesse $v_{c}.$ $(01\;point)$

 

4.4.3 Le choc a lieu dans une chambre à bulle qui permet de visualiser les trajectoires des particules chargées. 

 

On peut donc mesurer les rayons des trajectoires. 

 

Les charges du noyau et du proton sont égales. 

 

Déterminer alors la masse $m_{n}$ du noyau et donner le nom du nucléide correspondant. $(0.5\;point)$

 

On donne :

 

$R_{p}=\dfrac{5}{2}\;cm\;;\ R'_{n}=\dfrac{10}{3}\;cm\;;\ R'_{p}=\dfrac{5}{6}\;cm.$

 

4.5 Le proton entre enfin dans une région où règne un champ électrostatique uniforme $\overrightarrow{E}$ parallèle au vecteur $\overrightarrow{i}$ (du repère $(O\;,\ \vec{i}\;,\ \vec{j})$ avec une vitesse $\overrightarrow{v}=\overrightarrow{v'_{p}}.$

 

4.5.1 Établir l'équation de la trajectoire du proton dans le repère $(o\;,\ \vec{i}\;,\ \vec{j}).$ $(0.5\;point)$

 

4.5.2 Le proton traverse le trou $K$ de coordonnées $x_{k}=y_{k}=2R'p.$

 

Montrer que l'intensité du champ électrostatique a pour expression $E=\dfrac{m_{p}v_{c}^{2}}{18qR'_{p}}.$ $(0.75\;point)$

 

 

 

Données : 

 

masse molaire de l'iode $131$ : $M=131\;g\;mol^{-1}$ ;

 

nombre d'Avogadro : $N=6.02\cdot10^{23} mol^{-1}$

 

L'iode participe à la synthèse des hormones thyroïdiennes ; il est donc indispensable à l'organisme humain. 

 

L'assimilation de l'iode $127$, non radioactif, se fait sous forme d'ions iodure $(I^{-})$ dans la glande thyroïde. 

 

Lors des accidents nucléaires, il ya émission dans l'atmosphère, d'iode $131$,

radioactif $\beta^{+}.$ Sa période radioactive est $T=8.1$ jours. 

 

Cet iode $131$, $\left(^{131}_{53}I\right)$, donne au cours de sa désintégration, du xénon $\left(^{131}_{54}X_{e}\right).$

 

5.1 Écrire l'équation de la réaction de désintégration de l'iode $131.$

 

Préciser le type de radioactivité correspondant à cette désintégration. $(0.5\;point)$

 

5.2 La population vivant auprès d'une centrale nucléaire a reçu, sous forme d'iodure de potassium, $(KI)$, des comprimés d'iode $127$, à prendre en cas d'accident.

 

Justifier cette mesure de prévention. $(0.5\;point)$

 

5.3 L'iode $131$ est aussi utilisé en médecine pour l'examen des glandes surrénales par scintigraphie.

 

Définir puis déterminer l'activité d'un échantillon d'iode $131$ de masse $m=1.0\;g.$ $(01\;point)$

 

5.4 Pour l'examen par scintigraphie envisagé, on utilise une solution d'iode $131$ d'activité $A_{0}=3.7\cdot10^{7} B_{q}.$ 

 

Calculer la masse $m'$ d'iode $131$ à injecter au patient. $(01\;point)$

 

5.5 Tracer la courbe de décroissance de l'activité, au cours du temps, du produit utilisé. 

 

Déterminer graphiquement la date à laquelle l'activité de ce produit sera divisée par $10.$ $(01.5\;point)$