Bac Physique Chimie 1er Groupe S2 S2A S4 S5 2010

 

Données : 

 

masses molaires en $g\cdot mol^{-1}$ : 

 

$M_{C}=12$ ; 

 

$M_{H}=1$ ; 

 

$M_{O}=16$ ; 

 

$M_{Na}=23$ ; 

 

$M_{N}=14$

Un professeur de lycée cherche à faire identifier un acide carboxylique par un groupe d'élèves de son établissement. 

 

Pour cela il fait dissoudre $7.43\;g$ de l'acide, noté $AH$, dans $1\;L$ d'eau pure. 

 

De la solution ainsi préparée, les élèves prélèvent un volume $V=20\;mL$, qu'ils dosent avec une solution d'hydroxyde de sodium de concentration $C_{b}=0.1mol\cdot L^{-1}.$ 

 

En notant $V_{b}$ le volume de la solution d'hydroxyde de sodium versé dans la solution d'acide, ils obtiennent le tableau de mesures suivant, dans les conditions standard :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline V_{b}(mA)&0&1&2&3&6&10&12&15&17&19\\ \hline pH&3.0&3.7&4.0&4.2&4.5&4.9&5.1&5.3&5.6&6.2\\ \hline \end{array}$$

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline V_{b}(mA)&19.5&20&20.5&21&23&25&27&30\\ \hline pH&6.5&8.7&11.0&11.3&11.8&12.0&12.1&12.2\\ \hline \end{array}$$

 

1.1 Faire le schéma annoté du dispositif expérimental permettant de réaliser le dosage de la solution d'acide. $(0.75\;pt)$

 

1.2 Écrire l'équation de la réaction entre l'acide $AH$ et la solution d'hydroxyde de sodium. $(0.25\;pt)$

 

1.3 Tracez la courbe $pH=f(V_{b})$ (à rendre avec la feuille de copie).

 

Échelles : en abscisses $1\;cm$ pour $2\;mL$ ; en ordonnées $1\;cm$ pour $1$ unité de $pH.$ $(0.75\;pt)$

 

1.4 Déterminer la concentration de la solution de l'acide carboxylique $AH$ et le $pK_{a}$ du couple $AH/A^{-}.$ $(0.5\;pt)$

 

1.5 En déduire la masse molaire et la formule brute de l'acide $AH$ $(01\;pt)$

 

1.6 Le professeur donne aux élèves un extrait d'une liste d'acides avec les $pKa$ des couples correspondants.

$$\begin{array}{|c|c|} \hline \text{Noms}&pKa\text{ du couple}\\ \hline \text{Acide chloroéthanoïque}&2.87\\ \hline \text{Acide benzoïque}&2.40\\ \hline \text{Acide propanoïque}&4.90\\ \hline \text{Acide méthanoïque}&3.80\\ \hline \end{array}$$

 

Identifier l'acide $AH$ à partir des informations du tableau. 

 

Ce résultat est il en accord avec la formule brute trouvée à la question 1.5 ? $(0.75\;pt)$

Les protéines sont les macromolécules communément appelées polypeptides qu'on peut obtenir par des réactions de condensation des acides $\alpha$-animés. 

 

Elles jouent un rôle fondamental en biologie en assurant des fonctions diverses. 

 

Certaines d'entre elles ont une fonction hormonale, d'autres une fonction enzymatique c'est-à dire catalytique dans l'évolution de certaines synthèses biologiques.

 

Dans ce qui suit, on étudie un exemple de réaction de condensation d'acides $\alpha$-aminés et la cinétique de la réaction d'hydrolyse de protéines catalysée par des enzymes.

 

2.1 La leucine est un acide $\alpha$-aminé de formule semi-développée :

 

 

 

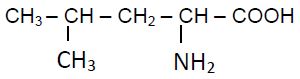
2.1.1 Donner, en nomenclature systématique, le nom de la leucine. $(0.25\;pt)$

 

2.1.2 Cette molécule de la leucine est-elle chirale ? 

 

(Justifier la réponse). $(0.25\;pt)$

 

2.1.3 Donner les représentations de Fischer des deux énantiomères de la leucine. $(0.25\;pt)$

 

2.1.4 Écrire la formule semi-développée de l'amphion correspondant à la molécule de la leucine. $(0.25\;pt)$

 

2.2 On fait réagir la leucine avec un acide $\alpha$--miné $A$ de formule :

 

 ;

 

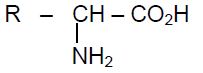
où $R$ est un radical alkyle ou un atome d'hydrogène.

 

Dans cette réaction la leucine est $N$-terminale (son groupement amine est bloqué). 

 

On obtient un dipeptide $P$ dont la masse molaire est égale à $188\;g\cdot moL^{-1}.$

 

2.2.1 Écrire, à l'aide des formules semi-développées ci-dessus, l'équation-bilan de la réaction de condensation qui se produit. $(0.75\;pt)$

 

2.2.2 Déterminer $R$ puis la formule semi-développée et le nom, en nomenclature officielle, de l'acide $\alpha$-aminé $A.$ $(01\;pt)$

 

2.3 La réaction inverse de la réaction de condensation est appelée hydrolyse. 

 

Dans les organismes vivants, les polypeptides des protéines provenant de l'alimentation sont hydrolysés en présence de catalyseurs : les enzymes. 

 

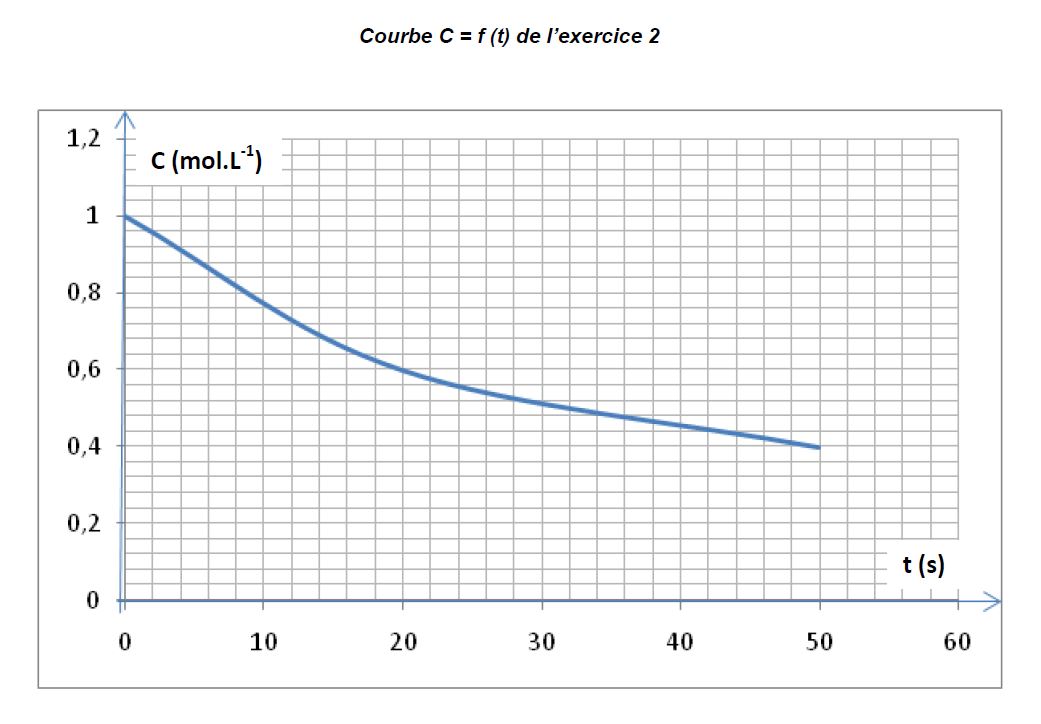
On suit la concentration molaire $C$ d'une protéine dont l'hydrolyse commence à la date $t=0.$ 

 

La courbe jointe en annexe (page 4) représente les variations de la concentration $C$ en fonction du temps $t.$

 

2.3.1 A quel instant la vitesse instantanée de disparition de la protéine est-elle maximale ? $(0.25\;pt)$

 

2.3.2 Déterminer graphiquement la vitesse instantanée aux dates $t_{0}=0$ et $t_{1}=20s.$ $(0.75\;pt)$

 

2.3.3 Déterminer graphiquement le temps de demi-réaction $t^{\dfrac{1}{2}}$ $(0.25\;pt)$

il n'est pas exigé de rendre la courbe avec la feuille de copie ; on explicitera simplement la méthode utilisée pour répondre à chaque question.

Données : 

 

Constante de gravitation $G=6.67\cdot10^{-11}$ $S.I$, 

 

masse de la Terre $M_{T}=6\cdot10^{24} kg$,

 

Rayon de la terre $R_{T}=6400\;km$, 

 

distance Terre-Soleil $d=1.5\cdot10^{8} km.$

 

3.1 Deux corps ponctuels $A$ et $B$, de masses respectives $m$ et $m'$, séparés par une distance $d$, s'attirent selon la loi de la gravitation universelle.

 

Rappeler l'expression de l'intensité des forces d'interaction gravitationnelle, s'exerçant entre les corps $A$ et $B.$ $(0.25\;pt)$

 

3.2 Dans l'espace, le soleil, la Terre et autres astres, peuvent être considérés comme des corps ponctuels. 

 

Le Soleil exerce sur la Terre une force de gravitation d'intensité $F=3.5\cdot10^{22} N.$

 

Déterminer la valeur de la masse du Soleil. $(0.5\;pt)$

 

3.3 Dans le champ de gravitation, un satellite de la Terre, en mouvement dans le plan de l'équateur, y effectue un mouvement circulaire uniforme à l'altitude $h_{1}=400\;km.$

 

3.3.1 Préciser le référentiel d'étude du mouvement de ce satellite. $(0.25\;pt)$

 

3.3.2 Exprimer la vitesse linéaire $V$ de ce satellite, puis calculer sa valeur. $(0.5\;pt)$

 

3.3.3 Établir les expressions littérales de la période $T$ et de la vitesse angulaire $\omega$ du satellite dans ce même repère. 

 

Faire l'application numérique. $(01\;pt)$

 

3.4 Entre autres conditions, un satellite de la Terre est géostationnaire si la période de son mouvement vaut $86400s.$

 

Justifier cette valeur de la période. $(0.25\;pt)$

 

3.5 Exprimer puis calculer l'altitude $h$ d'un satellite géostationnaire. $(0.75\;pt)$

La bobine et le condensateur sont deux composants électriques courants, utilisés dans les circuits les plus divers :

 

Microprocesseurs d'ordinateurs, horloges électroniques, émetteurs et récepteurs radios et télé, amplificateurs, etc...

 

L'objectif visé dans cet exercice est d'étudier la charge d'un condensateur et sa décharge à travers une bobine.

 

4.1 Un condensateur de capacité $C=1\mu F$, initialement déchargé est placé en série avec un conducteur ohmique de résistance $R=10k\Omega$, un interrupteur $K$ et un générateur $G$ de résistance négligeable qui maintient entre ses bornes une tension constante $U_{0}=5V.$

 

Le circuit est schématisé ci-contre (figure 1)

 

 

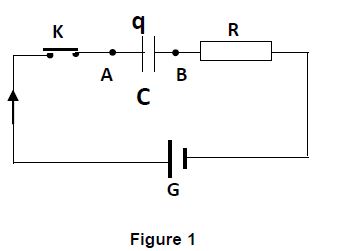
L'interrupteur $K$ est fermé à la date $t=0.$

 

Le sens d'orientation choisi est indiqué sur le schéma et $q$ désigne la charge de l'armature liée à $A.$

 

Établir l'équation différentielle vérifiée par la tension $u_{AB}(t)$ au cours de cette étape de charge du condensateur. $(0.5\;pt)$

 

4.2 Vérifier que $u_{AB}(t)=U_{0}\left(1-\mathrm{e^{-\dfrac{t}{\tau}}}\right)$ est solution de l'équation

différentielle précédemment établie, relation où $\tau$ est une constante que l'on exprimera en fonction de $R$ et $C.$ 

 

Calculer $\tau.$ $(01\;pt)$

 

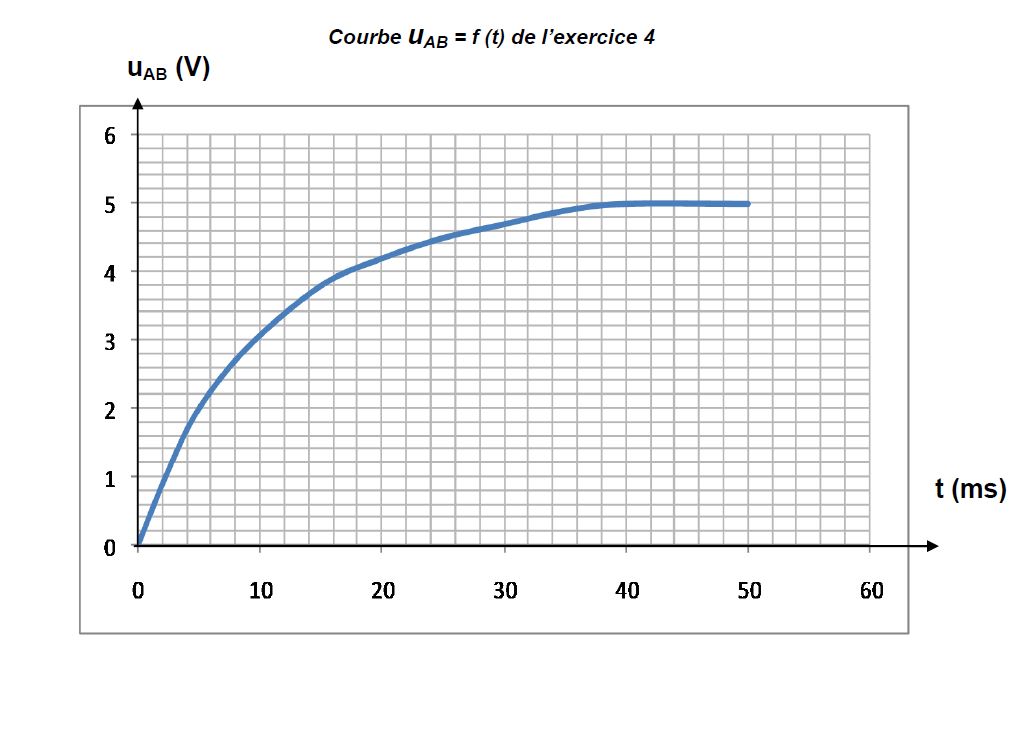
4.3 Afin de vérifier expérimentalement la loi de variation de $u_{AB}(t)$ et de déterminer la valeur de $\tau$ , on relève la valeur de $u_{AB}$ à différentes dates $t.$ 

 

Ce qui a permis de tracer la courbe $u_{AB}=f(t)$

 

jointe en annexe (page 4)

 

4.3.1 L'allure du graphe obtenu est-il en accord avec l'expression de $u_{AB}(t)$ donnée en 4.2 ? $(0.5\;pt)$

 

4.3.2 En utilisant la courbe, déterminer la valeur de $\tau$ (il n'est pas exigé de rendre la courbe avec la feuille de copie ; on pourra simplement expliciter la méthode utilisée pour déterminer $\tau).$

 

Comparer le résultat à la valeur théorique trouvée en 4.2 et conclure. $(0.75\;pt)$

 

4.4 Exprimer l'intensité instantanée du courant électrique $i(t)$ en fonction de $\dfrac{\mathrm{d}u_{AB}}{\mathrm{d}t}$, dérivée première de $u_{AB}(t)$ en fonction du temps. 

 

En déduire l'expression de $i(t)$ en fonction de $U_{0}$, $R$, $C$ et $t.$

 

Représenter l'allure de la courbe $i(t)=f(t).$ $(01\;pt)$

 

4.5 A la date $t=0$, le condensateur précédent, chargé sous la tension $U_{0}=5V$, est déchargé à travers une bobine d'inductance $L$ et de résistance négligeable (figure 2)

 

 

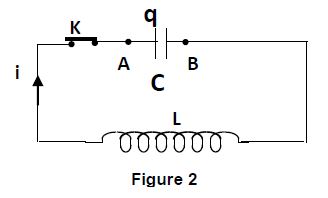
4.5.1 Établir l'équation différentielle traduisant les variations de la charge $q(t)$ du condensateur. $(0.5\;pt)$

 

4.5.2 En déduire alors l'expression littérale puis numérique de la charge du condensateur en fonction du temps.

 

Calculer la période des oscillations électriques du circuit.

 

On prendra $L=10\;mH$ $(0.75\;pt)$

En $1859$, en collaboration avec $R$ Brunsen, $G$ Kirschhoff publie trois lois relatives à l'émission et à l'absorption de lumière par les gaz, les liquides et les solides. 

 

Pour le cas de l'hydrogène, cette émission (ou absorption) de lumière correspondant à des transitions électroniques entre niveaux d'énergie, l'énergie d'un niveau étant donnée par la relation :

 

$E_{n}=-\dfrac{E_{0}}{n^{2}}$ avec $E_{0}=13.6eV$, et $n$ est le nombre quantique principal.

 

5.1 Préciser, pour l'atome d'hydrogène, le niveau de plus basse énergie correspondant à l'état fondamental. $(0.5\;pt)$

 

5.2 L'atome d'hydrogène peut passer d'un état excité de niveau $p$ à un autre de niveau $n<p$ en émettant des radiations. 

 

Exprimer, en fonction de $E_{0}$, $h$, $n$ et $p$, la fréquence des radiations émises par l'atome d'hydrogène lors de cette transition. $(0.75\;pt)$

 

5.3 Dans certaines nébuleuses, l'hydrogène émet des radiations de fréquences $v=4.57\cdot10^{14}Hz.$

 

Ces radiations correspondent à une transition entre un niveau excité d'ordre $p$ et le niveau d'ordre $n=2.$ 

 

Déterminer la valeur de $p$ correspondant au niveau excité. $(0.5\;pt)$

 

5.4 Une série de raies correspond à l'ensemble des radiations émises lorsque l'atome passe des différents niveaux excités $p$ au même niveau $n.$ 

 

Pour l'hydrogène, on a, entre autres, les séries de raies de Lyman $(n=1)$, de Balmer $(n=2)$ et de Paschen $(n=3)$,

 

5.4.1 Dans une série de raies, la raie ayant la plus grande fréquence dans le vide, est appelée raie limite, et sa fréquence est appelée fréquence limite.

 

Montrer que pour l'atome d'hydrogène, la fréquence limite d'une série de raies est donnée par :

 

$v_{lim}=\dfrac{E_{0}}{h\,n^{2}}.$ $(01\;pt)$

 

5.4.2 Calculer la fréquence limite pour chacune des séries de Lyman, de Balmer et de Paschen $(0.75\;pt)$

 

On donne : 

 

Constante de Planck $h=6.63\cdot10^{-34}J\cdot s$ ; 

 

célérité de la lumière dans le vide $C=3\cdot10^{8} m/s$

 

charge élémentaire $e=1.6\cdot10^{-19}C.$