Vous êtes ici

Bac Physique Chimie 1er Groupe S2 S2A S4 S5 2011

Données :

masses molaires atomiques :

$M(C)=12\;g\cdot mol^{-1}$ ;

$M(O)=16\;g\cdot mol^{-1}$ ;

$M(H)=1\;g\cdot mol^{-1}.$

Exercice 1 (04 points)

L'alcool amylique est un composé couramment utilisé en synthèse, en particulier pour la synthèse de l'arome de banane, lui même utilisé pour parfumer des médicaments et des boissons.

La formule brute de l'alcool amylique est de la forme

$C_{n}H_{2n+2}O.$

Deux des isomères de l'alcool amylique, notés

$A$ et

$B$ , ont la même chaîne carbonée et sont des alcools primaires.

L'isomère

$A$ est optiquement actif ; l'isomère

$B$ peut réagir avec l'acide éthanoïque pour donner un ester ayant une odeur de banane.

1.1 On procède à l'oxydation ménagée d'une masse

$m=1.72\;g$ de l'isomère B par un excès d'une solution acidifiée de permanganate de potassium.

Le produit obtenu est dissous dans de l'eau distillée.

On obtient alors une solution

$S$ de volume

$V=375\;mL.$

En présence d'un indicateur coloré approprié, on dose un volume

$V_{a}=10\;mL$ de la solution

$S$ par une solution d'hydroxyde de sodium de concentration

$C_{b}=2.9\cdot10^{-2} mol\cdot L^{-1}.$

Le virage de l'indicateur a lieu lorsqu'on a versé un volume

$V_{b}=18\;mL$ de la solution d'hydroxyde de sodium.

1.1.1 Déterminer la concentration

$C_{a}$ de la solution

$S.$

$(0.5\;point)$

1.1.2 En déduire la masse molaire et la formule brute de l'alcool amylique.

$(0.75\;point)$

1.1.3 La molécule de

$A$ contient un atome de carbone asymétrique.

a) Qu'appelle-t-on atome de carbone asymétrique ?

$(0.25\;point)$

b) Écrire la formule semi développée de

$A$ ; donner le nom de ce composé.

$(0.5\;point)$

1.1.4 Écrire la formule semi développée de

$B$ ; donner son nom.

$(0.5\;point)$

1.2 En présence d'acide sulfurique et en chauffant à reflux, on fait réagir

$16\;g$ d'acide éthanoïque avec

$8\;g$ de l'isomère

$B.$

Le composé organique formé a une masse

$m'=7\;g.$

1.2.1 Préciser le rôle de l'acide sulfurique dans cette réaction.

$(0.25\;point)$

1.2.2 Écrire l'équation-bilan de la réaction, nommer le composé organique obtenu.

$(0.5\;point)$

1.2.3 Le mélange initial est-il dans les proportions stoechiométriques ?

Si non préciser le réactif limitant, justifier

$(0.25\;point)$

1.2.4 Calculer le rendement de la réaction.

$(0.5\;point)$

Exercice 2 (04 points)

On dissout une certaine masse d'un acide carboxylique noté

$AH$ dans de l'eau distillée pour obtenir une solution

$S_{A}$ de volume

$V_{A}=50.0\;mL$ que l'on dose à l'aide d'une solution d'hydroxyde de sodium à

$4.17\cdot10^{-2} mol\cdot L^{-1}.$

$pH$ -mètre permet de suivre l'évolution du

$pH$ du mélange en fonction du volume

$V$ de la solution d'hydroxyde de sodium versé dans la solution

$S_{A}.$

On obtient la courbe (figure 1)

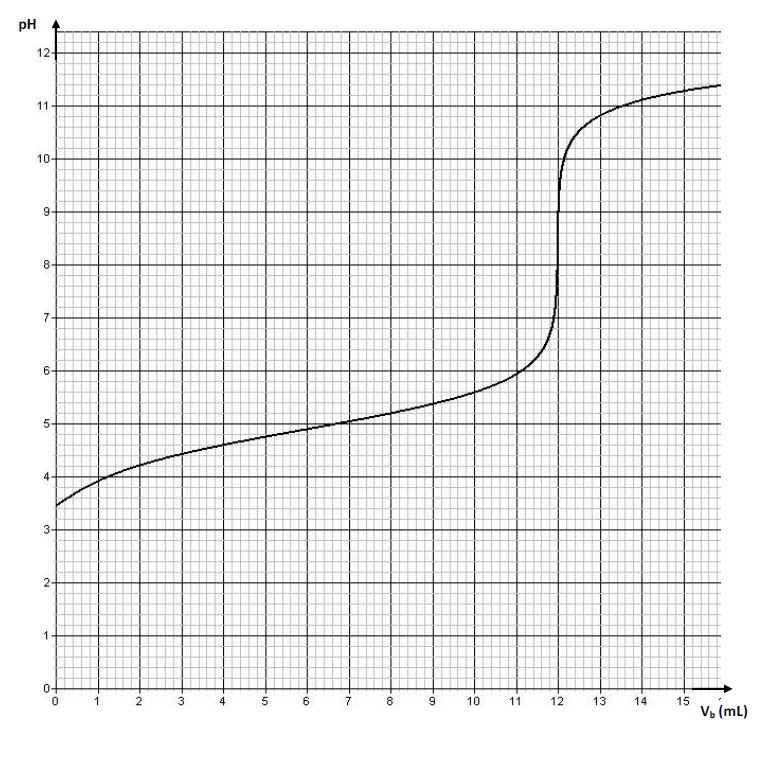
La température est supposée constante et égale à

$25^{\circ}C.$

2.1 Déterminer les coordonnées du point d'équivalence (Il n'est pas demandé de rendre la courbe avec la feuille de copie; on expliquera simplement la méthode utilisée).

$(0.75\;point)$

2.2 Écrire l'équation-bilan de la réaction du dosage.

$(0.5\;point)$

2.3 Déterminer la concentration molaire volumique de la solution

$S_{A}$

$(0.5\;point)$

2.4 Pour déterminer le

$pK_{A}$ du couple

$AH/A^{-}$ deux élèves utilisent des méthodes différentes.

2.4.1 L'un des élèves étudie la composition de la solution obtenue à la demi-équivalence.

Il en déduit une relation simple entre le

$pH$ et le

$pK_{A}$ et détermine alors le

$pK_{A}$ par méthode graphique.

a) Établir la relation entre le

$pK_{A}$ et le

$pH$ de la solution à la demi-équivalence.

$(0.5\;point)$

b) Retrouver la valeur du

$pK_{A}$ trouvée par cet élève (la courbe n'est pas à rendre).

$(0.25\;point)$

2.4.2 L'autre élève considère la solution obtenue à l'équivalence.

Il explique le caractère basique de cette solution en considérant la réaction entre l'ion carboxylate et l'eau.

Il montre alors, en négligeant la concentration de l'acide formé par ladite réaction devant celle de l'ion carboxylate, que la constante d'acidité peut s'exprimer par :

$K_{A}=\dfrac{\left[H_{3}O^{+}\right]^{2}\cdot C_{A}V_{A}}{K_{e}\left(V_{A}+V_{BE}\right)}$ , relation où

$V_{BE}$ représente le volume de la solution d'hydroxyde de sodium à l'équivalence et

$K_{e}$ le produit ionique de l'eau.

a) Écrire l'équation de la réaction entre l'ion carboxylate et l'eau.

$(0.5\;point)$

b) Retrouver l'expression de la constante d'acidité établie par l'élève.

En déduire la valeur du

$pK_{A}$ que cet élève a pu trouver.

Comparer avec la valeur trouvée en 2.4.1.b)

Commenter

$(01\;point)$

Exercice 3 (04 points)

On se propose de déterminer le nombre de masse de l'un des isotopes du potassium, élément chimique, mélange de deux types d'isotopes :

$^{39}K$

$^{x}K$ .

L'isotope

$^{39}K$ est plus abondant.

On utilise alors un spectrographe de masse constitué essentiellement de trois compartiments (figure 2)

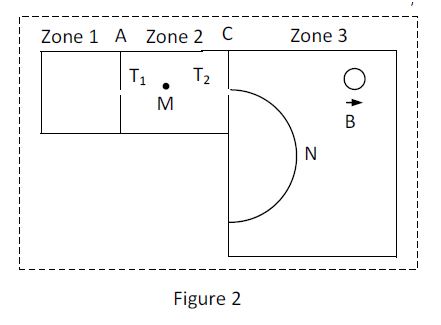
Dans le premier compartiment, les atomes de potassium sont ionisés en cations

$\left(^{39}K^{+}\text{ et }^{x}K^{+}\right)$ ; dans le deuxième compartiment, les ions sont accélérés, leurs vitesses initiales étant négligeables et dans le troisième compartiment, les ions sont soumis à l'action d'un champ magnétique ; en fin de course, ils atteignent un écran luminescent.

Données :

Le mouvement des particules a lieu dans le vide ; le poids d'un ion est négligeable devant la force électrique et la force magnétique.

La charge élémentaire est

$e=1.6\cdot10^{-19}C$ ;

la tension

$U$ établie entre les plaques

$A$ et

$C$ a pour valeur

$U=V_{A}-V_{C}=1.0\cdot10^{3} V$ ;

l'intensité du champ magnétique régnant dans la zone

$3$ est

$B=100\;mT$ ;

la masse d'un nucléon est

$m_{0}=1.67\cdot10^{-27}kg$ ;

la masse de l'ion

$^{39}K^{+}$ est

$m_{1}=39\;m_{0}$ ,

la masse de l'ion

$^{x}K^{+}$ est

$m_{2}=x\;m_{0}$

3.1 Entre les plaques

$A$ et

$C$ , les ions sont accélérés par un champ électrique uniforme.

Leur vitesse au point

$T_{1}$ de la plaque

$A$ est supposée nulle...

3.1.1 Reproduire la figure sur la feuille de copie et représenter la force électrique s'exerçant sur un ion potassium se trouvant en

$M.$

$(0.25\;point)$

3.1.2 Montrer que, arrivés au niveau de la plaque

$C$ , en

$T_{2}$ , tous les ions potassium ont la même énergie cinétique.

$(0.5\;point)$

3.1.3 Montrer alors qu'en

$T_{2}$ , la vitesse de chaque ion

$^{39}K^{+}$ a pour expression :

$V_{1}=\sqrt{\dfrac{2eU}{39\;m_{0}}}.$

En déduire, sans démonstration, l'expression de la vitesse

$V_{2}$ des isotopes

$^{x}K^{+}$ en

$T_{2}.$

$(0.5\;point)$

3.2 A partir de

$T_{2}$ , les ions pénètrent dans la zone

$3$ avec des vitesses perpendiculaires à la plaque

$C.$

Chaque type d'isotope effectue, dans le plan de la figure, un mouvement circulaire uniforme.

3.2.1 En un point

$N$ de l'une des trajectoires, représenter sur la figure déjà reproduite, la vitesse d'un ion potassium et la force magnétique qui s'exerce sur cet ion.

$(0.25\;point).$

3.2.2 Compléter la figure en représentant le sens du champ magnétique régnant dans la zone

$3.$

$(0.25\;point)$

3.3 Montrer que le rayon de la trajectoire des ions

$^{39}K^{+}$ a pour expression

$R_{1}=\dfrac{1}{B}\sqrt{\dfrac{78\;m_{0}U}{e}}$

En déduire l'expression du rayon

$R_{2}$ de la trajectoire des isotopes

$^{x}K^{+}.$

$(0.75\;point)$

3.4 Déterminer, par calcul, la valeur du rayon

$R_{1}$ de la trajectoire des ions

$^{39}K^{+}.$

$(0.25\;point)$

3.5 Les deux types d'isotopes rencontrent l'écran luminescent en deux points d'impact

$I_{1}$ et

$I_{2}$ ; le point d'impact

$I_{1}$ étant plus lumineux.

3.5.1 Préciser, en justifiant, le point d'impact de chaque type d'isotopes.

$(0.25\;point)$

3.5.2 Montrer que le rapport des rayons des trajectoires des isotopes du potassium dans la zone

$3$ est

$\dfrac{R_{1}}{R_{2}}=\sqrt{\dfrac{39}{x}}$

$(0.5\;point)$

3.5.3 La distance entre les points d'impact est

$d=2.5\;cm.$

Déterminer la valeur du nombre de masse

$x$ de l'isotope

$^{x}K^{+}.$

$(0.5\;point)$

Exercice 4 (04.5 points)

Sous le contrôle de leur professeur, un groupe d'élèves se propose de déterminer les caractéristiques électriques d'une bobine et d'un condensateur démontés d'un poste récepteur radio.

Ces élèves associent, en série la bobine

$(L\;,\ r)$ , le condensateur de capacité

$C$ , un conducteur ohmique de résistance

$R=80\Omega$ et un ampèremètre de résistance négligeable.

Aux bornes de cette association, ils branchent un générateur de basse fréquence

$(GBF)$ délivrant une tension sinusoïdale de valeur efficace

$U=3V$ et de fréquence

$N$ variable.

4.1 Représenter, par un schéma clair et annoté, le circuit électrique réalisé par ces élèves.

$(0.5\;point)$

4.2 Ces élèves font varier la fréquence

$N$ de la tension et notent la valeur de l'intensité efficace

$I$ du courant traversant le circuit.

Ils obtiennent le tableau suivant :

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline N(Hz)&800&820&840&850&860&863&870&880&890&900&920&940&1000\\ \hline I(mA)&7.1&10.1&16.8&23.1&29.4&30.0&27.5&20.7&15.4&12.1&8.3&6.3&3.7\\ \hline \end{array}$

4.2.1 Tracer la courbe représentant les variations de l'intensité efficace en fonction de le fréquence :

$I=f(N).$ Échelle :

$1\;cm\rightarrow 100\;Hz$ ;

$1\;cm\rightarrow 2.0\;mA.$

$(0.5\;point)$

4.2.2 Déterminer, graphiquement, la valeur

$N_{0}$ de la fréquence de la tension pour laquelle l'intensité efficace du courant atteint sa valeur maximale

$I_{0}$ que l'on précisera,

$(0.5\;point).$

4.2.3 Déduire, de l'expression de l'intensité efficace maximale

$I_{0}$ , la valeur de la résistance

$r$ de la bobine.

$(0.5\;point).$

4.3 La bande passante du circuit est délimitée par les fréquences, notées

$N_{1}$ et

$N_{2}$ , de la tension délivrée par le

$GBF$ et correspondant aux intensités efficaces

$I_{1}$ et

$I_{2}$ du courant telles que

$I_{1}=I_{2}=\dfrac{I_{0}}{\sqrt{2}}.$

4.3.1 Déterminer, graphiquement, la largeur de la bande passante de ce circuit.

$(0.5\;point)$

4.3.2 En déduire l'inductance

$L$ de la bobine.

$(0.5\;point)$

4.3.3 Calculer la valeur de la capacité

$C$ du condensateur.

$(0.5\;point)$

4.4 Pour vérifier que le mode de fonctionnement du circuit correspond à l'intensité efficace maximale du courant, les élèves branchent aux bornes du conducteur ohmique d'une part, aux bornes du

$GBF$ d'autre part, un oscillographe bicourbe.

Ils observent effectivement, sur l'écran de l'oscillographe, deux courbes disposées comme prévues.

4.4.1 Représenter le schéma du circuit en indiquant les branchements de l'oscillographe.

$(0.5\;point)$

4.4.2 Représenter, qualitativement, les courbes observées sur l'écran de l'oscillographe.

$(0.5\;point)$

Exercice 5 (03.5 points)

Un dispositif d'interférence est constitué d'une source lumineuse ponctuelle

$S$ éclairant deux fentes minces parallèles

$F_{1}$ et

$F_{2}$ et un écran d'observation

$E.$

La distance entre les fentes est notée

$a$ ; des fentes à l'écran d'observation la distance est

$D=1.0\;m.$

La source

$S$ est à égale distance des fentes

$F_{1}$ et

$F_{2}$ ; elle émet une lumière monochromatique de longueur d'onde

$\lambda=589\;nm$ (figure 3)

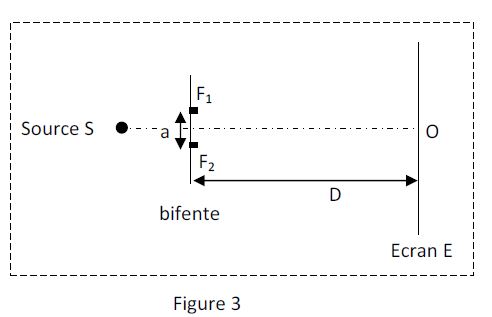
5.1 Représenter, sur un schéma, les faisceaux lumineux issus de la source

$S$ et des fentes

$F_{1}$ et

$F_{2}$ et indiquer clairement sur ce schéma la zone d'interférence.

$(0.5\;point)$

5.2 Représenter puis expliquer, sommairement, ce que l'on observe sur l'écran, au voisinage de

$O$ , point de l'écran situé sur la médiatrice de

$\left[F_{1}F_{2}\right].$

$(0.75\;point)$

5.3 Sur l'écran d'observation,

$20$ interfranges consécutifs couvrent une bande de largeur

$L=4.21\;mm.$

5.3.1 Rappeler l'expression de l'interfrange en fonction de la distance

$a$ entre les fentes, de la longueur d'onde

$\lambda$ de la lumière et de la distance

$D$ entre les fentes et l'écran d'observation :

$(0.25\;point)$

5.3.2 Calculer la distance

$a$ entre les fentes.

$(0.75\;point)$

5.4 La source

$S$ est remplacée par une source

$S'$ émettant deux radiations lumineuses monochromatiques de longueur d'onde respective

$\lambda_{1}=610\;nm\text{ et }\lambda_{2}$ inconnue.

On observe, sur l'écran, la superposition des systèmes d'interférences correspondant aux deux radiations.

5.4.1 Rappeler l'expression de la position, sur l'écran et par rapport au point

$O$ , d'une frange brillante.

$(0.25\;point).$

5.4.2 Montrer que les franges centrales des systèmes d'interférence coïncident.

$(0.25\;point).$

5.4.3 La frange brillante d'ordre

$10$ du système d'interférence correspondant à

$\lambda_{1}=610\;nm$ coïncide avec la frange brillante d'ordre

$11$ du système d'interférence correspondant à

$\lambda_{2}.$

Calculer la valeur de la longueur d'onde

$\lambda_{2}.$

L'ordre d'interférence de la frange centrale est

$0.$

$(0.75\;point)$

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Bac Physique Chimie 1er Groupe S2 S2A S4 S5 2011

Formulaire de recherche

Exercice 1 (04 points)

Exercice 2 (04 points)

Exercice 3 (04 points)

Exercice 4 (04.5 points)

Exercice 5 (03.5 points)

Ajouter un commentaire

Plain text