Bac Physique chimie 1er groupe S2-S2A-S4-S5 2021
Exercice 1
L'iodure de potassium est un sel de l'iode stable non radioactif.
L'iode stable est un élément nutritif essentiel dont la thyroïde a besoin en très petites quantités pour fonctionner correctement. Ainsi son absorption permet de se prémunir contre des maladies telles que le goitre et le cancer de la thyroïde.
Les ions iodure $\left(I^{-}\right)$ peuvent être également transformés par les ions péroxodisulfate $\left(S_{2}O_{8}^{2-}\right)$ en diiode $\left(I_{2}\right)$ selon l'équation-bilan suivante :
$$2I^{-}\ +\ S_{2}O_{8}^{2-}\ \rightarrow\ I_{2}\ +\ 2SO_{4}^{2-}$$
Dans cette transformation chimique, il est intéressant de constater que le diiode est la seule espèce chimique colorée, sa couleur en milieu aqueux jaune pale.
Le diiode prend une coloration bleue en présence d'empois d'amidon.
Au cours de la réaction entre les ions iodure et les ions péroxodisulfate, le mélange réactionnel devient de plus en plus jaune foncé puis marron.
Un groupe d'élèves, avec l'aide de leur professeur, étudie la cinétique de cette transformation chimique dans le laboratoire de leur lycée.
1.1 Quel est le passage du texte qui montre qu'il y a formation progressive du diiode.
1.2 Montrer que la transformation chimique précédente est une réaction d'oxydo-réduction.
On écrira les demi-équations électroniques redox puis on en déduira l'équation-bilan.
On donne les couples oxydant/réducteur mis en jeu :
$I_{2}/I^{-}$ et $S_{2}O_{8}^{2-}/SO_{4}^{2-}$
1.3 Le groupe a mélangé une solution d'iodure de potassium $KI$ de volume $V_{1}$ et de concentration $C_{1}$ avec une solution de péroxodisulfate de potassium $K_{2}S_{2}O_{8}$ volume $V_{2}$ et de concentration $C_{2}$, à un instant pris comme origine des dates.
Ce mélange est partagé en dix $(10)$ prélèvements de même volume chacun ; $V_{p}=10\,mL.$
Après dosages successifs du diiode contenu dans les prélèvements par une solution de thiosulfate de sodium $Na_{2}S_{2}O_{3}$ de concentration $C_{0}=0.1mol\cdot L^{-1}$, le groupe d'élèves trace la courbe $V_{0}=f(t)$ ; $\left(V_{0}\text{ étant le volume de la solution de thiosulfate versé à l'équivalence}\right).$ Il obtient la courbe ci-dessous. (voir figure 1).
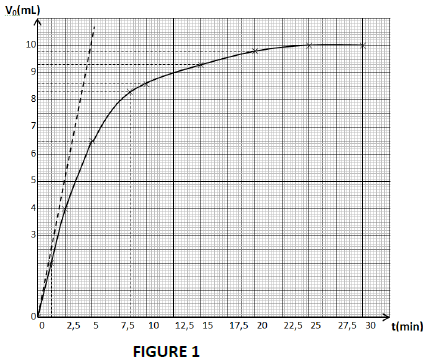
La droite en pointillée représente la tangente à l'origine de la courbe.
L'équation-bilan du dosage du diiode s'écrit :
$$I_{2}\ +\ 3S_{2}O_{3}^{2-}\rightarrow\ 2I^{-}\ +\ S_{4}O_{6}^{2-}$$
1.3.1 Dans chaque prélèvement, le groupe ajoute un peu d'empois d'amidon avant le dosage.
Quel est le rôle de l'empois d'amidon ?
1.3.2 Montrer que la quantité de matière de diiode totale formée dans le mélange réactionnel initial s'exprime par : $n\left(I_{2}\right)=5C_{0}V$
1.3.3 Définir la vitesse instantanée de formation du diiode, puis exprimer cette vitesse en fonction de $C_{0}$ et $V_{0}.$
Déterminer sa valeur maximale.
1.3.4 Déterminer la quantité de matière de $I_{2}$ formée lorsque la réaction entre les ions iodure $\left(I^{-}\right)$ et les ions péroxodisulfate $\left(S_{2}O_{8}^{2-}\right)$ est terminée.
1.3.5 Le groupe a introduit des quantités d'ions iodure et d'ions péroxodisulfate dans le mélange en proportions stoechiométriques.
Déterminer les valeurs de $C_{1}$ et $C_{2}$ sachant que $V_{2}=4V_{1}.$
Exercice 2
mases molaires atomiques en $g/mol$
$M(C)=12$ ;
$M(O)=12$ ;
$M(H)=1$
Certains produits utilisés pour laver les vitres contiennent des acides. Un laborantin propose d'étudier l'acide éthanoïque contenu dans un lave-vitre trouvé dans le marché.
Pour ce faire, Il réalise le dosage d'une solution de volume $V=50\,mL$ de ce produit par une solution d'hydroxyde de sodium de concentration $C_{b}= 0.1mol/L.$
Le dosage est suivi par $pH-$mètrie et on obtient les résultats suivants :
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline V_{b}(mL)&0&1.0&2.0&3.0&4.0&5.0&6.0&7.0&7.5&8.0&8.2&8.5&9.0&9.5&10.0&11.0&12.0\\ \hline pH&3.20&3.80&4.15&4.45&4.75&4.92&5.21&5.55&5.90&6.60&9.40&10.60&11.00&11.20&11.30&11.37&111.45\\ \hline \end{array}$$
2.1 Représenter et annoter le dispositif expérimental du dosage.
2.2 Tracer la courbe $pH=f\left(V_{b}\right)$, $V_{b}$ étant le volume d'hydroxyde de sodium ajouté.
Échelle :
$1\ cm\ \rightarrow\ 1\ \text{unité de }pH$
et $1\ cm\ \rightarrow\ 1\ mL$
2.3 Déterminer graphiquement les coordonnées du point équivalent.
En déduire la force de l'acide
2.4 Déterminer la concentration de l'acide dans le lave-vitre.
2.5 Déterminer graphiquement la valeur du $pKa$ du couple acide-base $\left(CH_{3}COOH/CH_{3}COO^{-}\right).$
2.6 Quelle est la forme prédominante si $pH=3.5$ et si $pH=6$ ?
2.7 On réalise l'estérification d'un mélange équimolaire de cet acide avec du propan$-2-$ol.
2.7.1 Écrire l'équation bilan de la réaction en utilisant les formules semi-développées.
2.7.2 Nommer le produit organique obtenu.
2.7.3 On considère que $60\%$ de l'alcool est estérifié et que sa masse volumique est de $786kg/m^{3}.$
Calculer la masse d'ester obtenue à partir d'un volume d'alcool de $40\,mL.$
Exercice 3
Des élèves de terminale $S$, à la suite de leur cours de dynamique, s'adonnent à un jeu qui consiste à lancer un solide dans une gouttière et à déterminer la position de chute sur le sol, s'il parvient à passer au-dessus d'un obstacle constitué d'une planche disposée verticalement. Le solide $(S)$, de dimensions négligeables et de masse $m=50\,g$, glisse sans frottement dans la gouttière $ABCD$ située dans le plan vertical. Le schéma simplifié du dispositif est représenté ci-dessous. (Voir figure 2)
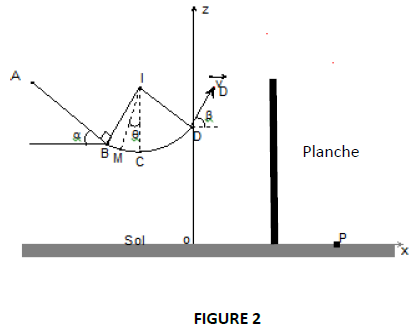
$AB$ est un plan incliné d'un angle $\alpha=30^{\circ}$ par rapport à l'horizontale. On donne $AB=1.6\,m.$
$BCD$ est un quart de cercle de centre $I$ de rayon $r=0.9\,m.$
Le point $C$ est situé sur la verticale passant par $I.$
Au premier essai, le solide est abandonné sans vitesse initiale au point $A.$
3.1 Déterminer la vitesse du solide aux points $B$, $C$ et $D.$
3. Exprimer l'intensité $R$ de la réaction exercée par la piste sur le solide $(S)$ au point $M$ situé entre $B$ et $C$ tel que $\left(\widehat{IM\;,\ IC}\right)=\theta$ en fonction de $V_{M}$, $r$, $g$, $\theta$ et
En déduire sa valeur au point $D$ où $\theta=60^{\circ}$
3.3 Le solide $(S)$ quitte la piste en $D$ avec la vitesse $V_{D}=3m\cdot s^{-1}$ faisant un angle $\beta=60^{\circ}$ avec l'horizontale.
Le point $D$ est situé à l'altitude $z_{D}=2m$ du sol horizontal.
3.3.1 Établir l'équation cartésienne de la trajectoire du mouvement de $(S)$ à partir de $D$ dans le repère $(O\;,\ x\;,\ z).$
3.3.2 La planche de hauteur $h=2.2\,m$ est située à l'abscisse $x=0.3\,m.$
Le solide passera-t-il au-dessus de la planche ?
3.3.3 Dans le cas où le solide passe au-dessus l'obstacle, déterminer la distance $OP$ où $P$ est le point d'impact du solide $(S)$ sur le plan horizontal.
3.4.4 En réalité le point d'impact du solide se situe à une distance $OP'= 0.8\,m.$
Déterminer la vitesse $\left(v'_{D}\right)$ du solide au point $D.$
En déduire l'intensité supposée constante des forces de frottement exercées par la piste $BCD$ sur le solide $(S).$
Exercice 4
Les circuits des appareils électriques utilisés dans plusieurs domaines de la vie courante (jouets, alarmes, télécommandes, chargeurs de téléphones,...) sont constitués de condensateurs, de bobines, de conducteurs ohmiques,...
Cet exercice a pour objectif l'étude de :
$-\ $La réponse d'un dipôle $RL$ soumis à une tension constante ;
$-\ $La réponse d'un dipôle $RC$ soumis à une tension constante ;
$-\ $La décharge oscillante d'un condensateur dans une bobine.
Pour cela, on réalise le montage schématisé ci-dessous constitué d'un générateur de f.é.m. $E=4.0V$, de deux conducteurs ohmiques de même résistance $R=1.0k\Omega$, d'une bobine d'inductance $L=1.0H$, d'un condensateur de capacité $C=2.2\cdot 10^{-6}F$ et de trois interrupteurs $K$ ; $K_{1}$ et $K_{2}.$
4.1 Étude du Dipôle $RL$
Les interrupteurs $K$ et $K_{1}$ sont fermés, $K_{2}$ ouvert.
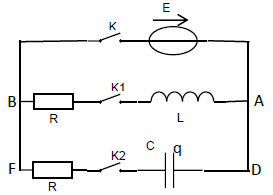
4.1.1 Qu'est-ce qu'un dipôle $RL$ ?
Que vaut la tension aux bornes du dipôle $RL$ de la branche $AB$ ?
4.1.2 Établir l'équation différentielle à laquelle obéit l'intensité $i_{1}$ du courant dans la branche $AB.$
4.1.3 Vérifier que l'expression de l'intensité $i_{1}=\dfrac{E}{r}\left(1-\mathrm{e}^{-\dfrac{t}{\tau}}\right)$ où $\tau$ est une constante à déterminer, est solution de l'équation différentielle.
Quelle est la signification physique de $\tau$ ?
4.2 étude du Dipôle $RC.$
Le condensateur est initialement déchargé. Les interrupteurs $K$ et $K_{2}$ sont fermés, $K_{1}$ ouvert.
4.2.1 Qu'est-ce qu'un dipôle $RC$ ?
Que vaut la tension aux bornes du dipôle $RC$ de la branche $DF$ ?
4.2.2 Établir l'équation différentielle à laquelle obéit la charge $q$ du condensateur.
4.2.3 Vérifier que l'expression $q=CE\left(1-\mathrm{e}^{-\dfrac{t}{\tau}}\right)$, où $\tau$ est une constante à déterminer, est solution de l'équation différentielle.
En déduire l'expression de l'intensité $i_{2}$ en fonction de la date $t.$
4.2.4 Exprimer l'énergie $\varepsilon$ stockée dans le condensateur à la fin de la charge.
4.3 Étude Dipôle $LC.$
Lorsque le régime permanent est établi dans le circuit, on ouvre l'interrupteur $K$ et on ferme les interrupteurs $K_{1}$ et $K_{2}$ à une date qui est choisie comme nouvelle origine des dates.
4.3.1 Quel est le sens de circulation du courant dans le circuit immédiatement après l'ouverture de l'interrupteur $K$ ?
4.3.2 Établir l'équation différentielle à laquelle obéit la charge $q.$
4.3.3 Que devient cette équation différentielle lorsque les résistances sont négligeables ?
Donner une solution de cette équation, puis calculer la période propre $T_{0}$ des oscillations électriques.
Exercice 5
Données :
$E_{0}=13.6eV$ ;
constante de Planck $h=6.62\cdot 10^{-34}J\cdot s$ ;
vitesse de la lumière dans le vide $c=3\cdot 10^{8}m/s$ ;
Constante de Rydberg $R_{H}=1.094\cdot 10^{7}/m$ ;
limites du spectre visible : $400\ nm\ldots\ldots 800\ nm$ ;
$D=4m$ et $S_{1}S_{2}=3mm.$
On se propose de déterminer une des longueurs d'onde du spectre d'émission de l'atome d'hydrogène par $2$ méthodes.
5.1. Première méthode : A partir des niveaux d'énergie de l'atome d'hydrogène.
Les niveaux d'énergie quantifiés de l'atome d'hydrogène sont donnés par la relation : $E_{n}=\dfrac{-E_{0}}{n^{2}}$ avec $n$ étant le nombre quantique principal. Il désigne le niveau de la couche.
5.1.1 Expliquer brièvement l'expression « niveaux d'énergie quantifiés de l'atome d'hydrogène ».
5.1.2 Que vaut $n$ quand l'atome d'hydrogène est dans son état fondamental ?
5.1.3 l'énergie d'ionisation d'un atome est l'énergie qu'il faut fournir à un atome neutre pour lui arracher un électron
5.1.3.1 Calculer, en électronvolts $(eV)$, l'énergie d'ionisation d'un atome d'hydrogène pris dans son état fondamental ?
5.1.3.2 Déterminer la longueur d'onde maximale de la radiation susceptible d'ioniser l'atome d'hydrogène.
5.1.4 Montrer que pour une transition entre un niveau d'énergie $E_{p}$ et un autre niveau d'énergie inférieur $E_{n}(n˂p)$, la relation donnant la longueur d'onde $\lambda$ de la radiation émise est : $\dfrac{1}{\lambda}=R_{H}\left(\dfrac{1}{n^{2}}-\dfrac{1}{p^{2}}\right).$
Calculer $\lambda$ pour $n=2$ et $p=5.$
Cette radiation est-elle visible ?
5.2 deuxième méthode : A partir des interférences lumineuses.
La radiation lumineuse émise par l'atome d'hydrogène lors de sa transition du niveau $p=5$ au niveau $n=2$ correspond à celle d'un laser utilisé pour éclairer deux sources secondaires $S_{1}$ et $S_{2}$ des fentes de Young. On observe des franges d'interférence sur un écran $E$ orthogonal au plan médiateur de $S_{1}S_{2}$ et situé à la distance $D$ de $S_{1}S_{2}.$
Soit $O$ la projection du milieu de $S_{1}S_{2}$ sur l'écran (voir figure 4).
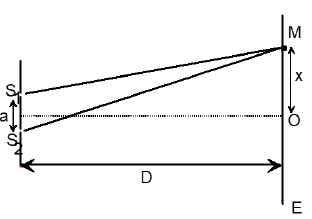
5.5.1 Établir l'expression de la différence de marche $\delta$ en un point $M$ du champ d'interférence tel que $\overline{OM}=x$, en fonction de $a$, $x$ et $D.$
5.5.2 Qu'appelle-t-on interfrange $i$ ?
5.5.3 La distance entre le point $O$ et le milieu de la $10^{ème}$ frange brillante est $d=5.8\,mm.$
Calculer l'interfrange $i.$
En déduire la longueur d'onde $\lambda$ de la radiation.

Ajouter un commentaire