Bac Physique chimie 2e groupe S1, S2 2024

 

On désire synthétiser le dipeptide noté $P_{1}$ de formule semi-développée :

 

 

1.1. Recopier la formule semi-développée de $P_{1}$ et encadrer la liaison peptidique.

 

1.2. Écrire les formules semi-développées des acides $\alpha-$aminés à utiliser pour la synthèse de $P_{1}.$

 

1.3. Écrire l'équation-bilan de la réaction de synthèse de $P_{1}.$

Une solution aqueuse contient à la date $t=0$ de l'éthanoate de méthyle de concentration molaire $10^{-2}mol/L$ et de l'hydroxyde de sodium de concentration molaire $10^{-2}mol/L.$

 

La réaction se fait suivant le schéma :

 

$CH_{3}CO_{2}CH_{3}\ +\ OH^{-}\ \longrightarrow\ CH_{3}CO_{2}^{-}\ +\ CH_{3}OH.$

 

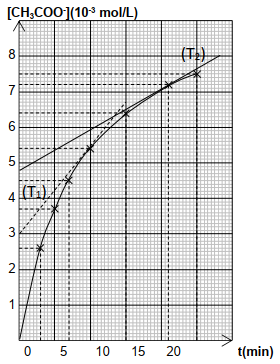
L'étude cinétique de cette réaction a permis de tracer la courbe donnant l'évolution de la concentration des ions éthanoate en fonction du temps (voir courbe ci-dessous).

 

 

2.1. Donner le nom de la réaction. 

 

Quelles sont ses caractéristiques ?

 

2.2. Déterminer graphiquement la vitesse de formation des ions éthanoate aux dates : $t_{1}=10\,min$ et $t_{2}=20\,min.$ Justifier qualitativement l'évolution de la vitesse.

Une solution d'acide benzoïque $C_{6}H_{5}COOH$ molaire a le même $pH$ qu'une solution d'acide chlorhydrique dont la concentration en ion $H_{3}O^{+}$ est $0.008\,mol\cdot L^{-1}.$

 

3.1. Calculer le $pH$ de la solution d'acide benzoïque.

 

3.2. Trouver les concentrations des différentes espèces présentes dans la solution d'acide benzoïque et en déduire son $pka.$ 

 

On donne $Ke=10^{-14}.$

Les composantes du vecteur accélération d'un point mobile sont $\overrightarrow{a}\left\lbrace\begin{array}{lcl} \ddot{x}&=&0\\\ddot{y}&=&-3\\\ddot{z}&=&0 \end{array}\right.$

 

A l'instant $t=0$, le mobile est en $M_{0}\left\lbrace\begin{array}{lcl} x_{0}&=&1\\y_{0}&=&2\\z_{0}&=&0 \end{array}\right.$ et son vecteur vitesse initial est $\overrightarrow{v_{0}}\left\lbrace\begin{array}{lcl} \dot{x}_{0}&=&1\\\dot{y}_{0}&=&1\\\dot{z}_{0}&=&0 \end{array}\right.$

 

$(x\ ;\ y\text{ et }z\text{ sont en mètres}).$

 

4.1. Établir les équations horaires du mouvement du mobile.

 

4.2. Déterminer l'équation cartésienne de la trajectoire du mobile, puis donner sa nature.

 

4.3. Calculer l'altitude maximale atteinte par le point mobile. 

 

Comment nomme-t-on cette altitude

Un noyau d'uranium $235$, sous l'impact d'un neutron se scinde en $2$ noyaux : un noyau de krypton $90$ et un noyau de baryum $143$, avec libération de neutrons. 

 

L'équation de la réaction nucléaire s'écrit : $_{92}^{235}U\ +\ _{0}^{1}n\ \longrightarrow\ _{Z}^{90}Kr\ +\ _{56}^{143}Ba\ +\ x_{0}^{1}n$

 

5.1. De quel type de réaction nucléaire s'agit-il ?

 

5.2. Déterminer les valeurs de $x$ et $Z.$

 

5.3. Calculer l'énergie libérée par cette réaction.

 

Données :

 

Masses en unité de masse atomique $(u)$ : 

 

$m(\text{neutron})=m_{n}=1.00866$ ;

 

$m(\text{proton})=m_{p}=1.00728$ ; 

 

$m(\text{uranium})=m_{U}=234.99332$ ; 

 

$m(\text{krypton})=m_{Kr}=89.89972$ ;

 

$m(\text{baryum})=m_{Ba}=142.88982.$

 

Unité de masse atomique $(u)$ : $1u=931.5\,MeV\cdot c^{-2}.$

Alimenté sous une tension sinusoïdale de pulsation $\omega_{0}$ (pulsation à la résonance d'intensité), un circuit $(R\;,\ L\;,\ C)$ en série a un facteur de qualité $Q=3.$ 

 

Sa bande passante est de $45\pi$ $\text{rad}\cdot s^{-1}$ et lorsque la tension efficace est de $15000\,mV$ alors il est parcouru par un courant d'intensité efficace égale à $250\,mA.$

 

6.1. Déterminer les valeurs de $R\;,\ L\;,\ \omega_{0}\text{ et }C.$

 

6.2. Trouver la valeur de la tension efficace aux bornes du condensateur à la résonance d'intensité.

On étudie à l'aide d'un teslamètre l'intensité $B$ du champ magnétique créé par un courant passant dans un solénoïde en son centre.

 

On utilise un solénoïde de longueur $\ell=0.80\,m$ comportant $N=768$ spires.

 

On obtient les résultats suivants :

$$\begin{array}{|l|c|c|c|c|} \hline I(A)&1.0&2.0&3.0&4.0\\ \hline B(T)&120\cdot 10^{-5}&240\cdot 10^{-5}&360\cdot 10^{-5}&480\cdot 10^{-5}\\ \hline \dfrac{B}{I}(A/T)&&&&\\\hline \end{array}$$

 

7.1. Recopier puis compléter le tableau ci-dessus. 

 

Déduire une relation numérique entre $B$ et $I.$

 

7.2. Dans la formule théorique liant $B$, $n$ et $I$ intervient un coefficient $\mu_{0}$ appelé perméabilité du vide.

 

7.2.1. Rappeler cette formule théorique.

 

7.2.2. Déduire des questions précédentes la valeur de $\mu_{0}.$

Les satellites météorologiques comme Méteosat$-8$ sont des appareils d'observation géostationnaires. 

 

Ce satellite a été lancé par ARIANE 5 le $28$ août $2002.$ 

 

Il est opérationnel depuis le $28$ janvier $2004.$ 

 

Il fournit de façon continue des informations couvrant une zone circulaire de la surface de la Terre.

 

8.1. Préciser les conditions à remplir par Méteosat$-8$ pour qu'il soit géostationnaire.

 

8.2. En déduire, pour Méteosat$-8$, la valeur du rayon $r=R_{T}+h$ de son orbite puis celle de son altitude $h.$

 

Données : 

 

période de révolution de la Terre autour de l'axe de ses pôles $T=86164\,s$ ; 

 

rayon de la Terre $R_{T}=6370\,km$ ; 

 

constante gravitationnelle $K=6.67\cdot 10^{-11}S.I.$ ;

 

masse de la Terre $M_{T}=5.98\cdot 10^{24}kg.$

$$\begin{array}{|l|c|c|c|c|c|c|c|c|} \hline \text{Questions}&Q_{1}&Q_{2}&Q_{3}&Q_{4}&Q_{5}&Q_{6}&Q_{7}&Q_{8}\\ \hline S_{1}-S_{3}(\text{ points})&2&2&2&3&3&2&3&3\\ \hline S_{2}-S_{4}-S_{5}(\text{ points})&2.5&3&2.5&2.5&2.5&2&3&2\\ \hline \end{array}$$