Corrigé Bac Maths S1 1er groupe 2014

1. L'événement $G$ :  "Obtenir deux boules de même couleur" est réalisé si et seulement si on a soit deux boules noires (événement $G_{n}$), soit deux boules blanches (événement $G_{b}$), soit deux boules rouges (événement $G_{r}$).

Puisque ces trois événements sont incompatibles, $$p(G)=p(G_{n}\cup G_{b}\cup G_{r})=p(G_{n})+p(G_{b})+p(G_{r})=\dfrac{C_{n}^{2}}{C_{9}^{2}}+\dfrac{C_{b}^{2}}{C_{9}^{2}}+\dfrac{C_{r}^{2}}{C_{9}^{2}}$$

c'est à dire $g(n,\ b,\ r)=\dfrac{C_{n}^{2}+C_{b}^{2}+C_{r}^{2}}{C_{9}^{2}}=\dfrac{1}{72}[n(n-1)+b(b-1)+r(r-1)]$

 

2. a. Notons $\vec{u}$ le vecteur $\overrightarrow{BN}\wedge\overrightarrow{RN}.$

$$\vec{u}=(9\vec{i}-9\vec{j})\wedge(9\vec{i}-9\vec{k})=81\vec{i}+81\vec{j}+81\vec{k}$$

Le vecteur $\vec{u}$ étant non nul, les trois points $N\;,\ B$ et $R$ ne sont pas alignés ; ils déterminent donc un plan ayant ce vecteur pour vecteur normal ou tout autre vecteur non nul qui lui est colinéaire, par exemple, le vecteur $\vec{u}_{0}$ de coordonnées (1, 1, 1).

On en déduit aussi que le plan $(NBR)$ a pour équation cartésienne $1\times x+1\times y+1\times z+d=0$, $d$ étant un réel à déterminer.

Pour connaître la valeur de $d$, il suffit d'exprimer que, par exemple, $N$ appartient au plan $(NBR)$ ; ce qui signifie que $9+d=0$ c'est à dire $d=-9$. On trouve donc que ce plan a pour équation $x+y+z-9=0$.

 

b. La somme de toutes les boules étant 9, on a $n+b+r=9$; donc le point $M$ appartient au plan $(NBR).$

 

c. Le point $M$ ayant pour coordonnées $(n,\ b,\ r)$, on a $OM^{2}=n^{2}+b^{2}+r^{2}$; donc   

\begin{eqnarray} g(n,\ b,\ r) & = & \dfrac{n(n-1)+b(b-1)+r(r-1)}{72} \nonumber \\ & = & \dfrac{n^{2}+b^{2}+r^{2}-n-b-r}{72} \nonumber \\ & = & \dfrac{OM^{2}-n-b-r}{72} \nonumber \\ & = & \dfrac{OM^{2}-9}{72} \nonumber \end{eqnarray}

 

d. $H$ est le projeté orthogonal de $O$ sur le plan $NBR$ signifie $\left\{\begin{array}{ll} \overrightarrow{OH} \text{ est colinéaire à }\vec{u}_{0} \\ H \text{ appartient au plan }(NBR) \end{array}\right.$

c'est à dire $\left\{\begin{array}{ll} \exists\;t\in\mathbb{R}\ :\ \overrightarrow{OH}=t\vec{u}_{0} \\ \text{les coordonnées de }H\text{ vérifient l'équation du plan }(NBR) \end{array}\right.$

Ce qui est équivalent à $\left\{\begin{array}{ll} \exists\;t\in\mathbb{R}\ :\ H\text{ a pour coordonnées } (t,\ t,\ t) \\ t+t+t-9=0 \end{array}\right.$

 

$\boxed{\text{Donc les coordonnées de }H\text{ sont }(3,\ 3,\ 3)}$

 

e. Pour que $g(n,\ b,\ r)$ soit minimale, il faut et il suffit que $OM^{2}$ le soit. $OM$ doit donc être minimale ; c'est à dire $M$ doit être égale à $H$ ou $n=b=r=3.$

Dans ce cas $g(n,\ b,\ r)=\dfrac{OM^{2}-n-b-r}{72}=\dfrac{3^{2}+3^{2}+3^{2}-9}{72}=\dfrac{1}{4}.$

 

3. a. Ici $g(n,\ b,\ r)=\dfrac{1}{4}$. La variable aléatoire $X$ prend des valeurs -1000 (si las deux boules tirées ne sont pas de même couleur) et $k-1000$ (si les deux boules tirées sont de même couleur) avec les probabilités respectives $1-g(n,\ b,\ r)=\dfrac{3}{4}\ $ et $\ g(n,\ b,\ r)=\dfrac{1}{4}.$

Par conséquent 

$$\boxed{E(X)=-1000\dfrac{3}{4}+(k-1000)\dfrac{1}{4}=\dfrac{k}{4}-1000}$$

 

b. Pour que le jeu soit équitable, il faut et il suffit que $E(X)=0$ c'est à dire $$\boxed{k=4000}$$

1. a. Si $n=1$, la propriété est triviale. Supposons donc $n\geq 2.$

\begin{eqnarray} a\wedge b^{n}=1 & \Leftrightarrow & \exists\;u,\ v\in\mathbb{Z}\ :\ au+b^{n}v=1\quad\text{ d'après Bezout } \nonumber \\ & \Rightarrow & au+bv'=1\quad\quad\text{ avec }v'=b^{n-1}v \nonumber \\ & \Rightarrow & a\wedge b=1 \nonumber  \end{eqnarray}

Réciproquement 

\begin{eqnarray} a\wedge b=1 & \Leftrightarrow & \exists\;u,\ v\in\mathbb{Z}\ :\ au+bv=1\quad\text{ d'après Bezout } \nonumber \\ & \Leftrightarrow & \exists\;u,\ v\in\mathbb{Z}\ :\ bv=1-au \nonumber \\ & \Rightarrow & b^{n}v^{n}=(1-au)^{n} \nonumber \\ & \Leftrightarrow & b^{n}v^{n}=\sum_{p=0}^{n}C_{n}^{p}a^{p}(-u)^{p} \nonumber  \end{eqnarray}

Tous les termes de la somme $\sum_{p=0}^{n}C_{n}^{p}a^{p}(-u)^{p}$ contiennent le facteur $a$ sauf le premier (correspondant à $p=0$) qui vaut 1 ; donc cette somme s'écrit $1+au'\;,\  u'\in\mathbb{Z}$ et 

\begin{eqnarray} a\wedge b=1 & \Rightarrow & b^{n}v'=1+au'\quad\text{ avec }v'=v^{n} \nonumber \\ & \Leftrightarrow & -au'+b^{n}v'=1\nonumber \\ & \Rightarrow & a\wedge b^{n}=1\quad\text{ d'après Bezout } \nonumber  \end{eqnarray}

 

b. Si $a$ et $b$ sont premiers entre eux, alors $a$ est premier avec $b^{n}$, d'après le a.

Comme $a$ divise le produit $b^{n}c$, il doit diviser $c$, d'après Gauss.

 

2. a. La fonction $f\ :\ x\mapsto\ 7x^{3}+2x^{2}+2x-5$ est définie sur $\mathbb{R}$, continue et dérivable et $\forall\;x\in\mathbb{R}\;,\ f'(x)=21x^{2}+4x+2.$

La dérivée est un polynôme du second degré en $x$ dont le discriminant réduit $2^{2}-42$ est strictement négatif ; la dérivée est alors strictement positive sur $\mathbb{R}.$ La fonction $f$ est donc une bijection de $\mathbb{R}$ sur $f(\mathbb{R})=\mathbb{R}$, cette dernière égalité provenant du fait que $\lim_{x\rightarrow +\infty}f(x)=+\infty\ $ et $\ \lim_{x\rightarrow -\infty}f(x)=-\infty.$

L'équation $f(x)=0$ admet donc une solution réelle unique.

$f(0)f(1)=-30<0$ donc la solution réelle de l'équation appartient à  $]0,\ 1[$, d'après le théorème des valeurs intermédiaires.

 

b. Si $p/q$ est solution de l'équation, on doit avoir $7\dfrac{p^{3}}{q^{3}}+2\dfrac{p^{2}}{q^{2}}+2\dfrac{p}{q}-5=0$ soit, en multipliant par $q^{3}$ : $$7p^{3}+2p^{2}q+2pq^{2}-5q^{3}=0$$

Cette relation s'écrit $$p(7p^{2}+2pq+2q^{2})=5q^{3}$$ 

donc $p$ divise $5q^{3}$ et d'après la question précédente, $p$ divise 5.

Cette relation s'écrit aussi $$7p^{3}=q(5q^{2}-2pq-2p^{2})$$

donc $q$ divise $7p^{3}$ et d'après la question précédente, $q$ divise 7.

 

c. Une éventuelle solution rationnelle de l'équation étant positive, on peut considérer que $p$ et $q$ sont positifs ; alors, les seules valeurs possibles de $p$ sont 1 et 5 et les seules valeurs possibles de $q$ sont 1 et 7. Comme en plus la solution appartient à l'intervalle $]0,\ 1[$, les seuls candidats solutions sont 1/7 et 5/7.

Un calcul direct montre que $$\boxed{\text{l'unique solution rationnelle de l'équation est 5/7}}$$

 

3. Ce qui précède montre que $7x-5$ est un facteur du polynôme  $7x^{3}+2x^{2}+2x-5.$

En procédant par identification ou par division euclidienne, on obtient $$7x^{3}+2x^{2}+2x-5=(7x-5)(x^{2}+x+1)$$

les autres solutions de l'équation sont donc celle de $x^{2}+x+1=0.$

Le discriminant de cette équation est $-3=(\mathrm{i}\sqrt{3})^{2}.$

$$\boxed{\text{les solutions complexes de l'équation sont donc }5/7\;,\ \mathrm{j}=\dfrac{-1+\mathrm{i}\sqrt{3}}{2}\text{ et }\overline{\mathrm{j}}=\dfrac{-1-\mathrm{i}\sqrt{3}}{2}}$$ 

Partie A

 

1. a. $$\forall\;x\in\;I\;,\ f_{1}(x)=\dfrac{1}{x}\int_{1}^{x}\dfrac{1}{t}\mathrm{d}t=\dfrac{1}{x}[\ln t]_{1}^{x}=\dfrac{\ln x}{x}$$

 

b. La fonction $f_{0}$ est définie, continue et dérivable sur $I$ et de dérivée $f'_{0}\ :\ x\mapsto\ -\dfrac{1}{x^{2}}$, fonction strictement négative.  

$\lim_{x\rightarrow +\infty}f_{0}(x)=0\ $ et $\ \lim_{x\rightarrow 0}f_{0}(x)=+\infty.$ Voici le tableau de variation de $f_{0}.$

 

$$\begin{array}{|c||lcr|} \hline x  & 0 &  & +\infty \\ \hline f'_{0}(x) &  & - &    \\ \hline  & +\infty  &   &    \\ f_{0}(x) &   &  \searrow &    \\  &   &  & 0  \\ \hline \end{array}$$

 

La fonction $f_{1}$ est définie, continue et dérivable sur $I$ et de dérivée $f'_{1}\ :\ x\mapsto\ \dfrac{1-\ln x}{x^{2}}.$ La dérivée est $\geq 0$ si et seulement si $\ln x\leq 1$ c'est à dire $x\leq\mathrm{e}$ et elle s'annule seulement si $x=\mathrm{e}.$

$\lim_{x\rightarrow +\infty}f_{1}(x)=0\ $ et $\ \lim_{x\rightarrow 0}f_{1}(x)=-\infty.$ Voici le tableau de variation de $f_{1}.$

 

$$\begin{array}{|c||lcccr|} \hline x  & 0 &  & \mathrm{e} &  & +\infty \\ \hline f'_{1}(x) &  & + & | &   &   \\ \hline  &   &   &  1/\mathrm{e} &  &  \\ f_{1}(x) &   &  \nearrow &   & \searrow &  \\  &  -\infty &  &  & &  0  \\ \hline \end{array}$$

 

2. \begin{eqnarray} \forall\;x\in\;I\;,\ f_{1}(x)-f_{0}(x)\geq 0 & \Leftrightarrow & \dfrac{\ln x}{x}-\dfrac{1}{x}\geq 0 \nonumber \\ & \Leftrightarrow & \ln x-1\geq 0 \nonumber \\ & \Leftrightarrow & x\qquad\quad \geq\mathrm{e} \nonumber  \end{eqnarray}

et $f_{1}(x)-f_{0}(x)=0$ seulement si $x=\mathrm{e}.$

Donc dans l'intervalle $]0,\ \mathrm{e}[$, $\mathcal{C}_{1}$ est au dessous de $\mathcal{C}_{0}$ et dans l'intervalle $]\mathrm{e},\ +\infty[$, $\mathcal{C}_{1}$ est au dessus de $\mathcal{C}_{0}.$

 

3. Voici les courbes de $\mathcal{C}_{1}$ et $\mathcal{C}_{0}.$

 

 

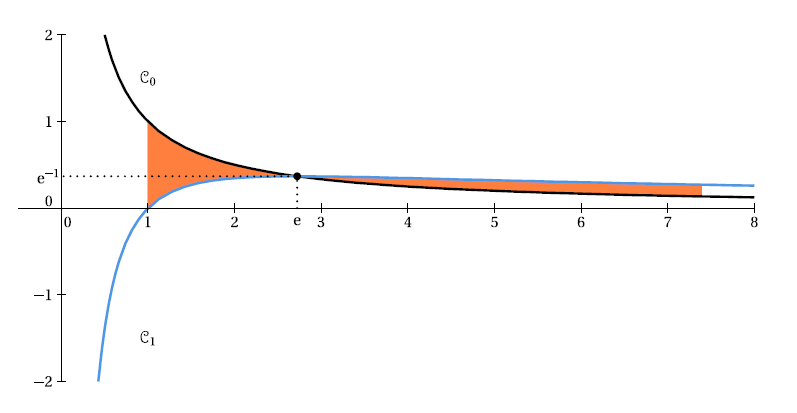
4. L'aire demandée vaut en unités d'aire $$\mathcal{A}=\int_{1}^{\mathrm{e}^{2}}|f_{1}(x)-f_{0}(x)|=\int_{1}^{\mathrm{e}}\left(\dfrac{1}{x}-\dfrac{\ln x}{x}\right)\mathrm{d}x+\int_{\mathrm{e}}^{\mathrm{e}^{2}}\left(\dfrac{\ln x}{x}-\dfrac{1}{x}\right)\mathrm{d}x$$

 

$f_{0}$ a pour primitives dans $I\;,\ x\mapsto\ \ln x+c_{te}.$

Pour tout $x\in\;I\;,\ f_{1}(x)=u'u$ avec $u=\ln x.$

Donc $f_{1}$ a pour primitives dans $I\;,\ x\mapsto\ \dfrac{1}{2}(\ln x)^{2}+c^{te}.$

$$\boxed{\mathcal{A}=\left[\ln x-\dfrac{1}{2}(\ln x)^{2}\right]_{1}^{\mathrm{e}}+\left[\dfrac{1}{2}(\ln x)^{2}-\ln x\right]_{\mathrm{e}}^{\mathrm{e}^{2}}=1-\dfrac{1}{2}+\left(\dfrac{1}{2}4-2-\left(\dfrac{1}{2}-1\right)\right)=1\;u.a=4\;cm^{2}}$$

 

Partie B

 

1. a. Appelons $\mathcal{P}_{n}$ la propriété "$f_{n}$ est dérivable sur $I.$"

Nous savons déjà que $f_{0}$ est dérivable sur $I\;;\ \mathcal{P}_{0}$ est donc vraie.

Supposons $\mathcal{P}_{n}$ vraie pour un entier $n$ donné, c'est à dire $f_{n}$ est dérivable sur $I.$

Alors l'application $g\ :\ x\mapsto\ \int_{1}^{x}f_{n}(t)\mathrm{d}t$ est dérivable sur $I$ et de dérivé $g'\ :\ x\mapsto\ f_{n}(x)$; par conséquent $f_{n+1}$, produit de $f_{0}$ et de $g$ est dérivable sur $I\;;\ \mathcal{P}_{n+1}$ est donc vraie.

 

b. D'après le a, pour tout entier naturel $n\;,\ f_{n+1}$ est dérivable sur $I$ et 

$$\boxed{\forall\;x\in\;I\;,\ f'_{n+1}=f'_{0}(x)g(x)+f_{0}(x)g'(x)=-\dfrac{1}{x^{2}}\int_{1}^{x}f_{n}(t)\mathrm{d}t+\dfrac{1}{x}f_{n}(x)=-\dfrac{1}{x}f_{n+1}(x)+\dfrac{1}{x}f_{n}(x)}$$

 

2. a. Soit $x$ un élément de $I$.

En intégrant la relation de la question précédente, on obtient $$\int_{1}^{x}f'_{n+1}(t)\mathrm{d}t=\int_{1}^{x}\dfrac{-f_{n+1}(t)+f_{n}(t)}{t} f_{n}(t)\mathrm{d}t$$

c'est à dire $$f_{n+1}(x)-f_{n+1}(1)=-F_{n+1}(x)+F_{n}(x)$$

 

ou, puisque $f_{n+1}(1)=0$

$$F_{n}(x)-F_{n+1}(x)=f_{n+1}(x)$$

 

b. Soit $p$ un entier naturel non nul et $x$ un élément de $I.$

En sommant la relation précédente de 0 à $p-1$ on obtient 

$$\sum_{n=0}^{p-1}f_{n+1}(x)=\sum_{n=0}^{p-1}(-F_{n+1}(x)-F_{n}(x))=-F_{p}(x)+F_{0}(x)$$

c'est à dire $$\sum_{n=1}^{p}f_{n}(x)=F_{0}(x)-F_{p}(x)$$

ou, en ajoutant $f_{0}$ aux deux membres $$\sum_{n=0}^{p}f_{n}(x)=f_{0}(x)+F_{0}(x)-F_{p}(x)$$

 

3. a. Pour tout entier naturel non nul $n$, appelons $\mathfrak{P}_{n}$ la propriété "$\forall\;x\in\;I\;,\ f_{n}(x)=\dfrac{\ln^{n}x}{n!x}.$"

Nous savons déjà que $\forall\;x\in\;I\;,\ f_{1}(x)=\dfrac{\ln x}{x}\;;\ \mathfrak{P}_{1}$ est donc vraie.

Supposons $\mathfrak{P}_{n}$ vraie pour un entier non nul $n$ donné, c'est à dire $\forall\;x\in\;I\;,\ f_{n}(x)=\dfrac{\ln^{n}x}{n!x}.$

Alors $$f_{n+1}(x)=\dfrac{1}{x}\int_{1}^{x}\dfrac{\ln^{n}t}{n!t}\mathrm{d}t$$

Mais pour tout $t$ dans $I\;,\ \dfrac{\ln^{n}t}{n!t}$ s'écrit $\dfrac{1}{n!}v^{n}v'$ avec $v=\ln t$, l'application $$t\mapsto\ \dfrac{1}{n!}\dfrac{1}{n+1}v^{n+1}=\dfrac{\ln^{n+1}t}{(n+1)!}$$

est donc une primitive $$t\mapsto\ \dfrac{\ln^{n}t}{n!t}$$

Par conséquent $\forall\;x\in\;I\;,\ f_{n+1}(x)=\dfrac{1}{x}\left[\dfrac{\ln^{n+1}t}{(n+1)!}\right]_{1}^{x}=\dfrac{\ln^{n+1}x}{(n+1)!x}\;;\ \mathfrak{P}_{n+1}$ est donc vraie.

 

b. Pour tout $x$ dans $x\in\;[1,\ \mathrm{e}]$, on a puisque la fonction $\ln$ est croissante : $0\leq\ln x\leq 1$, donc $$\forall\;x\in\;[1,\ \mathrm{e}]\;,\ |f_{n}(x)|=\dfrac{\ln^{n}x}{n!x}\leq \dfrac{1}{n!x}\leq \dfrac{1}{n!}$$

On en déduit que $$|F_{n}(\mathrm{e})|=\left|\int_{1}^{\mathrm{e}}\dfrac{f_{n}(t)}{t}\mathrm{d}t\right|\leq\int_{1}^{\mathrm{e}}\dfrac{|f_{n}(t)|}{t}\mathrm{d}t\leq\int_{1}^{\mathrm{e}}\dfrac{1}{n!t}\mathrm{d}t=\dfrac{1}{n!}[\ln t]_{1}^{\mathrm{e}}=\dfrac{1}{n!}$$

Puisque $\lim_{n\rightarrow +\infty}\dfrac{1}{n!}=0$, le théorème des gendarmes permet de conclure que $\lim_{n\rightarrow +\infty}F_{n}(\mathrm{e})=0$

 

c. De la question 2, on tire en remplaçant $x$ par $\mathrm{e}$ :

$$\sum_{n=0}^{p}f_{n}(\mathrm{e})=f_{0}(\mathrm{e})+F_{0}(\mathrm{e})-F_{p}(\mathrm{e})$$

et en faisant tendre $p$ vers $+\infty$

$$\lim_{p\rightarrow +\infty}\sum_{n=0}^{p}f_{n}(\mathrm{e})=f_{0}(\mathrm{e})+F_{0}(\mathrm{e})-\lim_{n\rightarrow +\infty}F_{p}(\mathrm{e})=f_{0}(\mathrm{e})+F_{0}(\mathrm{e})$$

soit en remplaçant $f_{n}(\mathrm{e})$ par $\dfrac{\ln^{n}\mathrm{e}}{n!\mathrm{e}}=\dfrac{1}{n!\mathrm{e}}$ et sachant que 

$$F_{0}(\mathrm{e})=\int_{1}^{\mathrm{e}}\dfrac{f_{0}(t)}{t}\mathrm{d}t=\int_{1}^{\mathrm{e}}\dfrac{1}{t^{2}}\mathrm{d}t=-\left[\dfrac{1}{t}\right]_{1}^{\mathrm{e}}=1-\dfrac{1}{\mathrm{e}}$$

$$\lim_{p\rightarrow +\infty}\sum_{n=0}^{p}\dfrac{1}{n!\mathrm{e}}=\dfrac{1}{\mathrm{e}}+1-\dfrac{1}{\mathrm{e}}=1$$

Et en multipliant par $\mathrm{e}$ :

$$\boxed{\lim_{p\rightarrow +\infty}\sum_{n=0}^{p}\dfrac{1}{n!}=\mathrm{e}}$$