Corrigé Bac Maths S1 1er groupe 2016
Exercice 1
1. L'application complexe $F$ correspondant à $f$ est de la forme $F(z)=az+b$ avec $a=\dfrac{1}{3}\mathrm{j}^{2}$ et $b=0$. C'est donc la similitude plane directe d'angle $\theta=arg\;a=2arg\;\mathrm{j}=\dfrac{4\pi}{3}$, de rapport
$k=|a|=\dfrac{1}{3}$ et de centre le point d'affixe $\dfrac{b}{1-a}=0$ c'est à dire l'origine.
2. a. Un point $M'$ d'affixe $z'$ appartient à $f(\mathcal{E})$ si et seulement si il existe un point $M$ de $\mathcal{E}$
d'affixe $z$ tel que $F(z)=z'$ c'est à dire $z=\dfrac{3}{\mathrm{j}^{2}}z'.$
Alors en tenant compte des indications sur $\mathrm{j}$ on a :
\begin{eqnarray} M'(z')\in f(\mathcal{E}) &\Leftrightarrow & M(z)\in\mathcal{E} \nonumber \\ &\Leftrightarrow &\mathrm{j}z^{2}+\overline{\mathrm{j}z^{2}}-\dfrac{10}{3}z\overline{z}+192 \qquad\qquad\qquad\qquad\qquad = 0\nonumber \\ &\Leftrightarrow & \mathrm{j}\left(\dfrac{3}{\mathrm{j}^{2}}z'\right)^{2}+\overline{\mathrm{j}\left(\dfrac{3}{\mathrm{j}^{2}}z'\right)^{2}}-\dfrac{10}{3}\dfrac{3}{\mathrm{j}^{2}}z'\overline{\left(\dfrac{3}{\mathrm{j}^{2}}z'\right)}+192= 0 \nonumber \\ &\Leftrightarrow & 9z'^{2}+\overline{9z'^{2}}-30z'\overline{z'}+192\qquad\qquad\qquad\quad\quad\ \ \ \ =0 \nonumber \\ &\Leftrightarrow & 3z'^{2}+\overline{3z'^{2}}-10z'\overline{z'}+64\qquad\qquad\qquad\qquad\quad\ \ \ =0 \nonumber \end{eqnarray}
Si $z'$ s'écrit $x'+\mathrm{i}y'$, alors
\begin{eqnarray}M'(z')\in f(\mathcal{E}) & \Leftrightarrow & 3(z'^{2}+\overline{z'^{2}})-10z'\overline{z'}+64\qquad\qquad\quad\ =0 \nonumber \\& \Leftrightarrow & 3\times2\mathbb{R}e(z'^{2})-10(x'^{2}+y'^{2})+64 \qquad=0 \nonumber \\& \Leftrightarrow & 3\times2(x'^{2}-y'^{2})-10(x'^{2}+y'^{2})+64\ \ \ =0 \nonumber \\& \Leftrightarrow & x'^{2}+4y'^{2}\qquad\qquad\qquad\qquad\qquad\qquad=16 \nonumber \end{eqnarray}
L'équation $x^{2}+4y^{2}=16$ est bien une équation cartésienne de $f(\mathcal{E}).$
b. Cette dernière équation s'écrit aussi $\dfrac{x^{2}}{4^{2}}+\dfrac{y^{2}}{2^{2}}=1.$
$f(\mathcal{E})$ est donc une ellipse de centre l'origine.
Ses foyers $F_{1}'$ et $F_{2}'$ ont pour coordonnées respectives $(-c,\ 0)$ et $(c,\ 0)$ avec $c=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$. Son excentricité est $e=\dfrac{c}{4}=\dfrac{\sqrt{3}}{2}$
3. Les foyers et axes de $\mathcal{E}$ sont les images réciproques des foyers et axes de $f(\mathcal{E})$ par la similitude réciproque de $f$, laquelle a pour centre $O$, pour angle $-\theta=-\dfrac{4\pi}{3}\equiv\dfrac{2\pi}{3}\;[2\pi]$ et pour
rapport $\dfrac{1}{k}=3.$
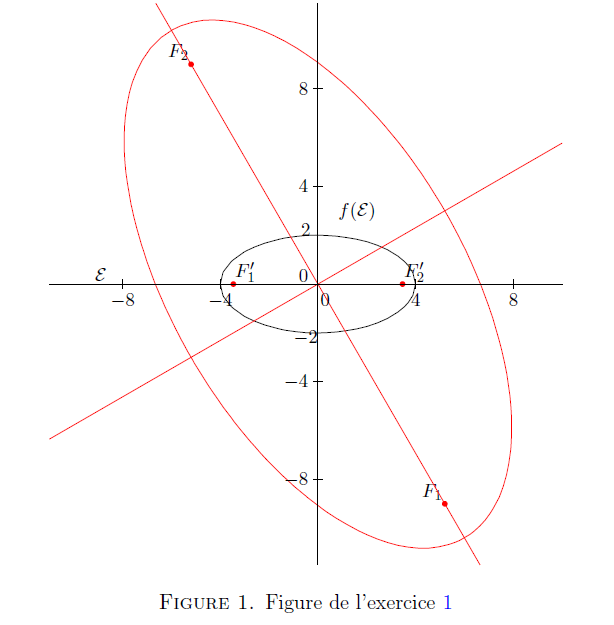
Voir les graphiques de $f(\mathcal{E})$ et de $\mathcal{E}$ dans la figure 1.
Exercice 2
Le nombre total de boules est $n+(8+n)+20=28+2n$.
1.
Notons $p_{N}\;,\ p_{B}$ et $p_{R}$ les probabilités de tirer une noire, une blanche et une rouge respectivement. Puisque les tirages sont avec remise, ces probabilités sont indépendantes du numéro
(premier ou second ) du tirage.
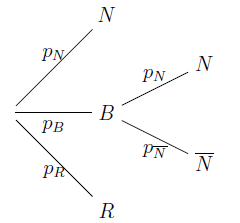
$$p_{N}=\dfrac{8+n}{28+2n}\;;\ p_{B}=\dfrac{20}{28+2n}\;;\ p_{R}=\dfrac{n}{28+2n}$$
Pour gagner, il faut avoir tiré une noire au premier tirage (probabilité $p_{N}$) ou avoir tiré une blanche au premier tirage et une noire au second tirage (probabilité $p_{B}\times p_{N}$). Donc la probabilité de gagner est $p_{N}+p_{B}\times p_{N}=\dfrac{(n+8)(n+24)}{2(n+14)^{2}}=f(n).$
2. a. Étudions d'abord les variations de $f.$
$f$ est continue et dérivable sur $\mathbb{R}_{+}^{*}$ et $\forall\;x\in\mathbb{R}_{+}^{*}\;,\ f(x)=2\dfrac{-x+16}{(x+14)^{3}}$. Voici son tableau de
variations.
$$\begin{array}{|c||lcccccr|}\hline x & 0 & & 1 & & 16 & & +\infty \\\hline f'(x) & & + & & + & 0 & - & \\\hline & & & & & 8/15 & & \\ & & & &\nearrow & &\searrow & \\ f & & & 1/2 & & & & \\& & \nearrow & & & & & 1/2 \\\hline\end{array}$$
On y voit nettement que f atteint un maximum égal à $\dfrac{8}{15}$ au point 16 (qui est heureusement un entier).
Pour que cette probabilité soit maximale, il faut donc et il suffit que $n=16$ et cette probabilité
vaut $\dfrac{8}{15}.$
b. La restriction de $f$ à $\mathbb{N}^{*}$ atteint un minimum égal à $\dfrac{1}{2}$ au point 1.
Pour que cette probabilité soit minimale, il faut donc et il suffit que $n=1$ et cette probabilité vaut $\dfrac{1}{2}.$
Quand $x$ tend vers $+\infty$, $f(x)$ tend vers $\dfrac{1}{2}$ mais cette valeur n'est pas atteinte par $f$ dans
l'intervalle $[16,\ +\infty[$
3. a. $X$ prend les valeurs $x_{1}=p-8\;,\ x_{2}=q-8$ et $x_{3}=-8$ avec les probabilités
$p_{1}=P(X=x_{1})=p_{N}=\dfrac{2}{5}$
$p_{2}=P(X=x_{2})=p_{B}\times p_{N}=\dfrac{2}{15}$
$p_{3}=P(X=x_{3})=1-p_{1}-p_{2}=\dfrac{7}{15}$
$\qquad=\text{ aussi }p_{R}+p_{B}\times p_{\overline{N}}=\dfrac{n}{28+2n}+\dfrac{20}{28+2n}\left(1-\dfrac{8+n}{28+2n}\right)$
L'espérance mathématique de $X$ est
$E(X)=p_{1}x_{1}+p_{2}x_{2}+p_{3}x_{3}=\dfrac{2}{5}(p-8)+\dfrac{2}{15}(q-8)+\dfrac{7}{15}(-8)=\dfrac{2}{5}p+\dfrac{2}{15}q-8$
b. La nullité de l'espérance mathématique signifie donc $3p+q=60.$
Le couple $(p_{0},\ q_{0})=(20,\ 0)$ est une solution "particulière" de l'équation diophantienne $3p+q=60$. La solution générale de cette équation est donc $$q=3k+q_{0}=3k\text{ et }p=-k+p_{0}=-k+20\;,\ k\in\mathbb{Z}$$
Les contraintes supplémentaires sur $p$ et $q$ deviennent $-k+20>3k>8$ c'est à dire $\dfrac{8}{3}<k<5$. $k$ vaut donc 3 ou 4 et les couples $(p,\ q)$ possibles sont $(17,\ 9)$ et $(16,\ 12).$
4. Pour $p=16$ et $q=12$, on sait d'après ce qui précède que l'espérance mathématique est
nulle. La variance vaut alors $V(X)=E(X^{2})-[E(X)]^{2}=E(X^{2})$
$$V(X)=p_{1}x_{1}^{2}+p_{2}x_{2}^{2}+p_{3}x_{3}^{2}=\dfrac{2}{5}8^{2}+\dfrac{2}{15}4^{2}+\dfrac{7}{15}8^{2}=\dfrac{18\times 16}{5}$$
Et l'écart type vaut $\sigma(X)=\sqrt{V(X)}=4\sqrt{\dfrac{18}{5}}$
Poblème
Partie A
1. a.
La fonction $\phi : x\mapsto x-1-\ln x$ est définie, continue et
dérivable sur $\mathbb{R}_{+}^{*}$ et $\forall\;x\in\mathbb{R}_{+}^{*}\;,\ \phi'(x)=1-\dfrac{1}{x}=\dfrac{x-1}{x}$
La dérivée s'annule au point 1 et est >0 si et seulement
si $x>1$. Voici le tableau de variations de $\phi .$
$$\begin{array}{|c||lcccr|}\hline x & 0 & & 1 & & +\infty \\\hline\phi'(x) & & - & 0 & + & \\\hline & & & & & \\\phi(x) & & \searrow & & \nearrow & \\ & & & 0 & & \\\hline\end{array}$$
On y voit nettement que la fonction $\phi$ est positive ; donc $\forall\;x\in\mathbb{R}_{+}^{*}\;,\ \ln x\leq x-1.$
Soit $x$ un réel>0 et $k$ un entier naturel non nul. Dans la relation précédente, en remplaçant $x$ par $\dfrac{x}{k}$, on a $\ln\dfrac{x}{k}\leq\dfrac{x}{k}-1$ puis par intégration :
$$\int_{k-1/2}^{k+1/2}\ln\dfrac{x}{k}\mathrm{d}x \leq\int_{k-1/2}^{k+1/2}\left(\dfrac{x}{k}-1\right)\mathrm{d}x=\left\lbrack\dfrac{x^{2}}{2k}-x\right\rbrack_{x=k-1/2}^{x=k+1/2}=0$$
$$\int_{k-1/2}^{k+1/2}\ln\dfrac{x}{k}\mathrm{d}x \leq\int_{k-1/2}^{k+1/2}\left(\dfrac{x}{k}-1\right)\mathrm{d}x=\left\lbrack\dfrac{x^{2}}{2k}-x\right\rbrack_{x=k-1/2}^{x=k+1/2}=0$$
b. En sommant les relations précédentes de $k=1$ à $k=n$ on a : $$\sum_{k=1}^{n}\int_{k-1/2}^{k+1/2}\ln\dfrac{x}{k}\mathrm{d}x\leq 0\text{ puis }\sum_{k=1}^{n}\int_{k-1/2}^{k+1/2}(\ln x-\ln k)\mathrm{d}x\leq 0$$
ensuite, avec la relation de Chasles : $$\int_{1/2}^{n+1/2}\ln x\mathrm{d}x-\sum_{k=1}^{n}\ln k\leq 0\text{ ou }\int_{1/2}^{n+1/2}\ln x\mathrm{d}x-\ln(n!)\leq 0$$
c. Comme $x\longmapsto x\ln x-x$ est une primitive de $x\longmapsto \ln x$ (résultat que l'on obtient par intégration par parties), $\left\lbrack x\ln x-x \right\rbrack_{1/2}^{n+1/2} -\ln(n!)\leq 0$ c'est à dire $\ln(n!)+n-\left(n+\dfrac{1}{2}\right)\ln\left(n+\dfrac{1}{2}\right)-\ln\sqrt{2}\geq 0$
2. a.
La fonction $g$ est définie, continue et dérivable sur $[0,\ 1[$ et $\forall\;x\in[0,\ 1[\;,\ g'(x)=\dfrac{2x}{(1-x^{2})^{2}}$
Voici le tableau de variations de $g.$
$$\begin{array}{|c|lcr|}\hline x & 0 & & 1 \\\hline g'(x) & & + & \\\hline & & & +\infty \\g(x) & & \nearrow & \\ & 1 & & \\\hline\end{array}$$
- Pour tout $x$ dans $]0,\ 1[$, la fonction $h$ est continue sur $[0,\ x]$, dérivable sur $]0,\ x[$ et pour tout
$u\in]0,\ x[$, $h'(u)=g(u)$. D'après le théorème des accroissements finis, il existe un réel $c$ dans
l'intervalle $]0,\ x[$ tel que $\dfrac{h(x)-h(0)}{x-0}=h'(c)$ c'est à dire $\dfrac{1}{x}\int_{0}^{x}g(t)\mathrm{d}t=g(c)\text{ ou }f(x)=g(c).$
Mais puisque la fonction $g$ est croissante $g(0)\leq g(c)\leq g(x)$ ; donc $1\leq f(x)\leq g(x).$
- Si on veut utiliser la valeur moyenne de $g$ on peut dire : La fonction $g$ étant continue, $\dfrac{1}{x}\int_{0}^{x}g(t)\mathrm{d}t$, valeur moyenne de $g$ sur $[0,\ x]$ est une valeur de $g$ ; il existe donc $c$ dans $[0,\ x]$ tel que $\dfrac{1}{x}\int_{0}^{x}g(t)\mathrm{d}t=g(c).$
La fonction $g$ étant continue, sa limite en 0 est $g(0)=1$. Alors les inégalités $1\leq f(x)\leq g(x)$
et le théorème des gendarmes entraînent que $f$ aussi a pour limite $1=f(0)$ quand $x$ tend vers 0 et donc oui ! $f$ est continue en 0.
c. Pour montrer qu'il existe deux réels $a$ et $b$ tels que $\forall\;t\in\mathbf{I}\;,\ g(t)=\dfrac{a}{1-t}+\dfrac{b}{1+t}$, il suffit de réduire au même dénominateur et d'identifier les numérateurs. On trouve $a=b=\dfrac{1}{2}$ puis $g(t)=\dfrac{1}{2}\left(\dfrac{1}{1-t}+\dfrac{1}{1+t}\right)$
On en déduit par intégration que
$\forall\;x\in]0,\ 1[\;,\ f(x)=\dfrac{1}{x}\int_{0}^{x}\dfrac{1}{2}\left(\dfrac{1}{1-t}+\dfrac{1}{1+t}\right)\mathrm{d}t=\dfrac{1}{2x}\left\lbrack\ln(1+t)-\ln(1-t)\right\rbrack_{0}^{x}=\dfrac{1}{2x}\ln\dfrac{1+x}{1-x}$
3. a. Un calcul direct montre que $\forall\;n\in\mathbb{N}^{*}$,
\begin{eqnarray} u_{n+1}-u_{n} & = & \ln\left[(n+1)! \right]-\left(n+1+\dfrac{1}{2}\right) \ln(n+1)+n+1-\ln(n!)+\left(n+\dfrac{1}{2} \right) \ln n-n \nonumber \\ & = & 1-\dfrac{2n+1}{2}\ln\dfrac{n+1}{n} \nonumber \\ & = & 1-f\left(\dfrac{1}{2n+1}\right) \nonumber \end{eqnarray}
Puisque pour tout $x$ de $[0,\ 1[$, $f(x)$ est $\geq 1$, cette dernière relation entraine que $\forall\;\in\mathbb{N}^{*}\;,\ u_{n+1}-u_{n}$ est $\leq 0$; la suite $(u_{n})$ est donc décroissante.
b.
\begin{eqnarray}\forall\;\in\mathbb{N}^{*}\;,\ u_{n} & = & \ln(n!)+n-\left(n+\dfrac{1}{2}\right)\ln n \nonumber \\ & \geq & \ln(n!)+n-\left(n+\dfrac{1}{2}\right)\ln(n+1)\quad\text{ car }\ln\text{ est croissante } \nonumber \\ & \geq & \ln\sqrt{2}\quad\text{ d'après la question 1.c } \nonumber \end{eqnarray}
c. La suite $(u_{n})$ étant décroissante et minorée est convergente.
Partie B
1. a.
$v_{1}=\int_{0}^{\frac{\pi}{2}}\sin t\mathrm{d}t=\left\lbrack-\cos t\right\rbrack_{0}^{\frac{\pi}{2}}=1$ $\forall\;\in\mathbb{N}^{*}\;,\ v_{n}$ est $\geq 0$
puisque intégrale d'une fonction continue $\geq 0.$
$v_{n+1}-v_{n}=\int_{0}^{\frac{\pi}{2}}\sin^{n} t(\sin t-1)\mathrm{d}t$ est $\leq 0$
puisque intégrale d'une fonction $\leq 0$. La suite $(v_{n})$ est donc décroissante.
b. Pour tout entier naturel $n$, en posant $u=\sin^{n+1} t$ et $v'=\sin t$, on a $u'=(n+1)\sin^{n} t\cos t$
et on peut prendre $v=-\cos t$ ; une intégration par parties donne alors :
\begin{eqnarray}v_{n+2} & = & \int_{0}^{\frac{\pi}{2}}\sin^{n+1} t\sin t\mathrm{d}t \nonumber \\ & = & \left\lbrack uv\right\rbrack_{0}^{\frac{\pi}{2}}+(n+1) \int_{0}^{\frac{\pi}{2}}\sin^{n} t\cos^{2} t\mathrm{d}t \nonumber \\ & = & (n+1)\int_{0}^{\frac{\pi}{2}}\sin^{n} t(1-\sin^{2} t)\mathrm{d}t \nonumber\\ & = & (n+1)(v_{n}-v_{n+2}) \nonumber \end{eqnarray}
Ce qui entraîne bien $v_{n+2}=\dfrac{n+1}{n+2}v_{n}$.
c. On a pour tout entier naturel $n$ :
\begin{eqnarray}\dfrac{n+1}{n+2} & = &\dfrac{v_{n+2}}{v_{n}} \nonumber\\ & \leq & \dfrac{v_{n+1}}{v_{n}}\quad \text{ car la suite }(v_{n})\quad\text{ est décroissante }\nonumber\\ & \leq & 1 \quad\text{ car la suite }(v_{n})\quad\text{ est décroissante }\nonumber\end{eqnarray}
Puisque $\dfrac{n+1}{n+2}$ a pour limite 1 quand n tend vers $+\infty$, le théorème des gendarmes appliqué à la relation $\dfrac{n+1}{n+2}\leq\dfrac{v_{n+1}}{v_{n}}\leq 1$
permet d'affirmer que $$\lim_{n\rightarrow+\infty}\dfrac{v_{n+1}}{v_{n}}=1$$
d. $\dfrac{a_{n+1}}{a_{n}}=\dfrac{(n+2)v_{n+2}v_{n+1}}{(n+1)v_{n+1}v_{n}}=1$; la suite $(a_{n})$ est donc constante. Cette constante est égale à $a_{0}=v_{1}v_{0}=\dfrac{\pi}{2}.$
e. $\forall\;n\in\mathbb{N}\;,\ \dfrac{n}{n+1}a_{n}\dfrac{v_{n}}{v_{n+1}}=\dfrac{n}{n+1}(n+1)v_{n+1}v_{n}\dfrac{v_{n}}{v_{n+1}}=nv_{n}^{2}.$
Comme la suite $(a_{n})$ est constante égale à $\dfrac{\pi}{2}$, la relation précédente s'écrit aussi : $nv_{n}^{2}=\dfrac{n}{n+1}\dfrac{v_{n}}{v_{n+1}}\dfrac{\pi}{2}$; donc $$\lim_{n\rightarrow+\infty}nv_{n}^{2}=\dfrac{\pi}{2}$$.
2. Pour tout entier naturel $n$, on pose $b_{n}=v_{2n}$
a. $nb_{n}^{2}=\dfrac{1}{2}2nv_{2n}^{2}=\dfrac{1}{2}\beta_{2n}\text{ avec }\beta_{n}=nv_{n}^{2}$. et puisque la suite $\beta_{n}$ a pour limite $\dfrac{\pi}{2}$, on peut
écrire d'après les indications de l'énoncé : $$\lim_{n\rightarrow+\infty}nb_{n}^{2}=\dfrac{1}{2}\lim_{n\rightarrow+\infty}\beta_{2n}=\dfrac{\pi}{4}$$
b. Pour tout entier naturel $n$, appelons $P_{n}$ la propriété : $b_{n}=\dfrac{(2n)!}{2^{2n}(n!)^{2}}\dfrac{\pi}{2}$
$b_{0}=v_{0}=\dfrac{\pi}{2}\;,\ P_{0}$ est donc vraie
Supposons $P_{n}$ vraie pour un entier donné $n$.
Alors, avec la relation $(E)$ on peut écrire :
\begin{eqnarray} b_{n+1} & = & v_{2n+2}=\dfrac{2n+1}{2n+2}v_{2n}=\dfrac{2n+1}{2n+2}b_{n} \nonumber\\ & = & \dfrac{2n+1}{2n+2}\dfrac{(2n)!}{2^{2n}(n!)^{2}}\dfrac{\pi}{2}\quad \text{ car }(P_{n})\quad\text{ est supposée vraie }\nonumber\\ & = & \dfrac{(2n+1)(2n+2)}{(2n+2)^{2}}\dfrac{(2n)!}{2^{2n}(n!)^{2}}\dfrac{\pi}{2} \nonumber\\ & = & \dfrac{[2(n+1)]!}{2^{2n+2}}[(n+1)!]^{2}\dfrac{\pi}{2} \nonumber\end{eqnarray}
$P_{n+1}$ est donc vraie.
3. a. Pour tout entier $n$ on a : $\mathrm{e}^{u_{n}}=\mathrm{e}^{\ln n!}\mathrm{e}^{n}\mathrm{e}^{-(n+1/2)\ln n}=n!\mathrm{e}^{n}n^{-n-1/2}=n!\left(\dfrac{\mathrm{e}}{n}\right)^{n}\dfrac{1}{\sqrt{n}}.$
b. Pour tout entier $n$ on a :
\begin{eqnarray}\mathrm{e}^{u_{2n}-2u_{n}} & = & \dfrac{\mathrm{e}^{u_{2n}}}{(\mathrm{e}^{u_{n}})^{2}} \nonumber\\ & = & (2n)!\left(\dfrac{\mathrm{e}}{2n}\right)^{2n}\dfrac{1}{\sqrt{2n}}\left[\dfrac{1}{n!}\left(\dfrac{n}{\mathrm{e}}\right)^{n}\sqrt{n}\right]^{2} \nonumber\\ & = & \dfrac{(2n)!}{2^{2n}(n!)^{2}}\sqrt{\dfrac{n}{2}} \nonumber\\ & = & \dfrac{1}{\pi}b_{n}\sqrt{2n}=\dfrac{\sqrt{2}}{\pi}\sqrt{nb_{n}^{2}} \nonumber\end{eqnarray}
La constante $A$ demandée vaut donc $\dfrac{\sqrt{2}}{\pi}$
On en déduit que $\mathrm{e}^{u_{2n}-2u_{n}}=\dfrac{\sqrt{2}}{\pi}\sqrt{nb_{n}^{2}}$ a pour limite $\dfrac{\sqrt{2}}{\pi}\sqrt{\dfrac{\pi}{4}}=\dfrac{1}{\sqrt{2\pi}}.$
Mais si $l$ est la limite de $(u_{n})$ alors $\mathrm{e}^{u_{2n}-2u_{n}}$ a aussi pour limite $\mathrm{e}^{l-2l}=\mathrm{e}^{-l}$.
Par conséquent $\mathrm{e}^{-l}=\dfrac{1}{\sqrt{2\pi}}$
c'est à dire $l=\ln\sqrt{2\pi}$ et $\mathrm{e}^{u_{n}}$ a pour limite $\mathrm{e}^{l}=\sqrt{2\pi}$
Figure 1. Figure de l'exercice 1
Source: Office du bac Sénégal

Ajouter un commentaire