Corrigé Bac Maths S1 S3 1er groupe 2011
Exercice 1 (4 pts)
1) $u_{0}=27\;,\ u_{1}=77\;,\ u_{2}=227\;,\ u_{4}=677$
Conjecturons que les deux derniers chiffres de un sont 27 ou 77
2) Puisque le premier terme $u_{0}$ est un entier, on montre facilement par récurrence que pour tout $n\in\mathbb{N}^{*}$, un est un entier.
On a pour tout $n\in\mathbb{N}^{*}\ :\ u_{n+2}=3u_{n+1}-4=3(3u_{n}-4)-4=9u_{n}-16$ ;
donc $u_{n+2}-u_{n}=8u_{n}-16=8(u_{n}-2)$
Ainsi $u_{n+2}-u_{n}$ est un multiple de 8 ; ce qui se traduit par $u_{n+2}\equiv u_{n}\;[8]$
En prenant pour $n$ un entier pair $2p\;,\ p\in\mathbb{N}^{*}$ cette relation se traduit par $u_{2(p+1)}\equiv u_{2p}\;[8]$
c'est à dire en posant pour tout $p\in\mathbb{N}^{*}\ :\ u_{2p}=a_{p}\ :\ a_{p+1}\equiv a_{p}\;[8]$
Deux termes consécutifs de la suite $(a_{p})$ sont donc congrus modulo 8 ; donc tous les termes sont congrus au premier terme $a_{0}=u_{0}=27$ qui lui-même est congru à 3. Conclusion $$u_{2n}\equiv 3\;[8]$$
En prenant pour $n$ un entier impair $2p+1\;,\ p\in\mathbb{N}^{*}$ cette relation se traduit par $u_{2(p+1)+1}\equiv u_{2p+1}\;[8]$
c'est à dire en posant pour tout $p\in\mathbb{N}^{*}\ :\ u_{2p+1}=b_{p}\ :\ b_{p+1}\equiv b_{p}\;[8]$
Deux termes consécutifs de la suite $(b_{p})$ sont donc congrus modulo 8 ; donc tous les termes sont congrus au premier terme $b_{0}=u_{1}=77$ qui lui-même est congru à 5. Conclusion $$u_{2n+1}\equiv 5\;[8]$$
3) On a pour tout $n\in\mathbb{N}^{*}\ :\ v_{n+1}=u_{n+1}-2=3u_{n}-6=3(u_{n}-2)=3v_{n}.$
La suite $(v_{n})$ est donc géométrique de raison 3 et de premier terme $v_{0}=u_{0}-2=25.$
Par conséquent, pour tout $n\in\mathbb{N}^{*}\ :\ v_{n}=3^{n}v_{0}$ c'est à dire $u_{n}=2+25\times 3^{n}$ ou $2u_{n}=4+50\times 3^{n}$
4) De cette relation on déduit $2u_{n}-54=50(3^{n}-1)$, ce qui entraîne : $2u_{n}-54\equiv[50]$
De plus $(3^{n}-1)$ est pair parce que $3^{n}$ est impair ; donc $2u_{n}-54$ est un multiple de $2\times 50=100$ c'est à dire $2u_{n}-54\equiv[100].$
Cette dernière relation se traduit par : il existe un entier $p$ tel que $2u_{n}-54+100p$ soit, $u_{n}=27+50p.$
Le nombre $50p$ se terminant par 50 ou 100, le nombre $u_{n}$ se termine par 27 + 50 = 77 ou 27 + 00 = 27
5) Remarquons d'abord que $u_{n}$ est impair parce que son écriture décimale se termine par 7 ; donc tous ses diviseurs sont impairs.
Soit $d$ un diviseur commun positif de $u_{n+1}$ et $u_{n}.$ Il existe deux entiers $p$ et $q$ (dépendant
de $n$) tels que $u_{n+1}=pd$ et $u_{n}=qd.$
La relation $u_{n+1}=3u_{n}-4$ qui définit la suite $(u_{n})$ devient $d(3q-p)=4.$
Ainsi $d$, qui est un nombre impair, divise 4 c'est à dire $d=1$ et $u_{n+1}$ et $u_{n}$ sont bien premiers entre eux.
On peut aussi dire : Si $a$ et $b$ sont deux entiers tels qu'il existe deux entiers $q$ et $r$ avec $a=bq+r$ alors $a\wedge b=b\wedge r$ et l'écriture $u_{n+1}=3u_{n}-4$ montre que $u_{n+1}\wedge u_{n}=u_{n}\wedge 4=1$ la dernière égalité provenant de ce que les seuls diviseurs positifs de 4 sont 1, 2 et 4 et $u_{n}$ est impair.
Exercice 2 (4 pts)
1) a) Pour montrer que $f$ est une isométrie, il suffit de vérifier qu'elle conserve la distance.
Soient $M(x_{M}\;,\ y_{M}\;,\ z_{M})$ et $N(x_{N}\;,\ y_{N}\;,\ z_{N})$ deux points quelconques de $\mathcal{E}$ et $M'(x_{M'}\;,\ y_{M'}\;,\ z_{M'})$
et $N'(x_{N'}\;,\ y_{N'}\;,\ z_{N'})$ leurs images respectives par $f$ c'est à dire
$$\left\lbrace\begin{array}{lcl} x_{M'} &=& y_{M} \\ y_{M'} &=& z_{M}+1 \\ z_{M'} &=& x_{M}-1 \end{array}\right.\quad\text{ et }\quad\left\lbrace\begin{array}{lcl} x_{N'} &=& y_{N} \\ y_{N'} &=& z_{N}+1 \\ z_{N'} &=& x_{N}-1 \end{array}\right.$$
Alors
\begin{eqnarray} M'N'^{2} &=& (x_{N'}-x_{M'})^{2}+(y_{N'}-y_{M'})^{2}+(z_{N'}-z_{M'})^{2} \nonumber \\ &=& (y_{N}-y_{M})^{2}+(z_{N}-z_{M})^{2}+(x_{N}-x_{M})^{2} \nonumber \\ &=& MN^{2} \nonumber \end{eqnarray}
b) Un point $M(x\;,\ y\;,\ z)$ de $\mathcal{E}$ est invariant si et seulement si $f(M)=M$ c'est à dire
$$\left\lbrace\begin{array}{lcl} x &=& y \\ y &=& z+1 \\ z &=& x-1\end{array}\right.$$
Ce système est donc équivalent à $x=y=z+1$
On reconnaît là un système d'équations d'une droite.
L'ensemble des points invariants par $f$ est la droite d'équations : $x=y=z+1$
Le point $A$ appartient manifestement à cette droite puisque $x_{A}=y_{A}=z_{A}+1$
Le point $B(1\;,\ 1\;,\ 0)$ appartient aussi `a cette droite puisque $x_{B}=y_{B}=z_{B}+1.$
Le vecteur $\vec{u}=\overrightarrow{AB}(1\;,\ 1\;,\ 1)$ est donc un vecteur directeur de cette droite
L'ensemble des points invariants par $f$ est bien la droite $\Delta.$
On peut aussi trouver un vecteur directeur de $\Delta$ en partant d'une représentation paramétrique de $\Delta.$
Prenons $z$ comme paramètre. La relation $x=y=z+1$ est équivalente à
$$\left\lbrace\begin{array}{lcl} x &=& t+1 \\ y &=& t+1 \\ z &=& t\end{array}\right.\;;\quad t\in\mathbb{R}$$
Le vecteur $\vec{u}(1\;,\ 1\;,\ 1)$ est donc un vecteur directeur de cette droite.
2) Étant donné que le point $A$ appartient à $P$,
pour prouver que le point $I$ appartient à $P$, il suffit d'établir que $\overrightarrow{AI}$ est orthogonal à $\vec{u}$ c'est à dire $\overrightarrow{AI}.\vec{u}=0.$
$\overrightarrow{AI}$ ayant pour coordonnées $(-1\;,\ 0\;,\ 1)$ on a bien : $\overrightarrow{AI}.\vec{u}= -1.1+0.0+1.1=0$
a) $I'=f(I)$ a pour coordonnées
$$\left\lbrace\begin{array}{lclcr} x_{I'} &=& y_{I} &=& 0 \\ y_{I'} &=& z_{I}+1 &=& 1 \\ z_{I'} &=& x_{I}-1 &=& -2\end{array}\right.$$
Étant donné que le point $A$ appartient à $P$,
pour prouver que le point $I'$ appartient à $P$, il suffit d'établir que $\overrightarrow{AI'}$ est orthogonal à $\vec{u}$ c'est à dire $\overrightarrow{AI'}.\vec{u}=0.$
$\overrightarrow{AI'}$ ayant pour coordonnées $(0\;,\ 1\;,\ -1)$ on a bien : $\overrightarrow{AI'}.\vec{u}= 0.1+1.1-1.1=0$
On peut aussi donner une équation de $P$ et établir que les coordonnées des points $I$ et $I'$ vérifient cette équation.
Puisque le vecteur $\vec{u}$ est normal à $P$, une équation cartésienne de $P$ sera de la forme $x+y+z+d=0.$
Dire que $A$ appartient $P$ signifie alors que $1+d=0$ c'est à dire $d=1.$
3) $f$ étant une isométrie de l'espace dont l'ensemble des points invariants est la droite
$\Delta$, elle est une rotation d'axe $\Delta.$ Son angle a pour mesure $\theta=(\overrightarrow{AI}\;,\ \overrightarrow{AI'}).$
Or $\overrightarrow{AI}.\overrightarrow{AI'}=AI.AI'\cos\theta\;;\ \overrightarrow{AI}$ a pour coordonnées $(-1\;,\ 0\;,\ 1)$ et $\overrightarrow{AI'}$ a pour coordonnées $(1\;,\ 0\;,\ -1).$
Donc $-1=\sqrt{2}\sqrt{2}\cos\theta$ c'est à dire $\cos\theta=-\dfrac{1}{2}$ ; on peut donc prendre
$$\theta=\dfrac{2\pi}{3}\quad\text{ou}\quad-\dfrac{2\pi}{3}\quad\text{(selon l'orientation de}\Delta)$$
4) a) Notons $Q_{1}$ l'ensemble des points $M$ de $\mathcal{E}$ d'images $M'$ tels que le milieu $J$ de $[MM']$ appartient au plan $Q$ d'équation $2x+y-z=0.$
Soit $M(x\;,\ y\;,\ z)$ un point de $\mathcal{E}$ et $M'(x'\;,\ y'\;,\ z')$ son image par $f$ c'est à dire
$$\left\lbrace\begin{array}{lcl} x' &=& y \\ y' &=& z+1 \\ z &=& x-1\end{array}\right.$$
Les coordonnées du milieu $J$ de $[MM']$ sont
$$x_{J}=\dfrac{1}{2}(x+x')\;,\ y_{J}=\dfrac{1}{2}(y+y')\;\text{ et }\;z_{J}=\dfrac{1}{2}(z+z')$$
$$x_{J}=\dfrac{1}{2}(x+y)\;,\ y_{J}=\dfrac{1}{2}(y+z+1)\;\text{ et }\;z_{J}=\dfrac{1}{2}(z+x-1)$$
Donc
\begin{eqnarray} M\in\;Q_{1} &\Leftrightarrow& J\in\;Q \nonumber \\ &\Leftrightarrow& 2(x+y)+(y+z+1)-(z+x-1)=0 \nonumber \\ &\Leftrightarrow& x+3y+2=0 \nonumber \end{eqnarray}
L'ensemble des points $M$ de $\mathcal{E}$ d'images $M'$ tels que le milieu $J$ de $[MM']$ appartient
au plan $Q$ d'équation $2x+y-z=0$ est donc le plan d'équation $x+3y+2=0.$
b) Notons $D_{1}$ l'ensemble des points $M$ de $\mathcal{E}$ d'images $M'$ tels que le milieu $J$ de $[MM']$ appartient à la droite $(D)$ d'équations $x=y=z.$
Soit $M(x\;,\ y\:,\ z)$ un point de $Q_{1}$ et $M'(x'\;,\ y'\;,\ z')$ son image par $f.$
Les coordonnées du milieu $J$ de $[MM']$ sont
$$x_{J}=\dfrac{1}{2}(x+y)\;,\ y_{J}=\dfrac{1}{2}(y+z+1)\;\text{ et }\;z_{J}=\dfrac{1}{2}(z+x-1)$$
Donc
\begin{eqnarray} M\in\;D_{1} &\Leftrightarrow& J\in\;(D) \nonumber \\ &\Leftrightarrow& x+y=y+z+1=z+x-1\quad(*) \nonumber \\ &\Leftrightarrow& \left\lbrace\begin{array}{rcl} x-z-1 &=& 0 \\ -x+y+2 &=& 0 \end{array}\right. \nonumber \end{eqnarray}
L'ensemble des points $M$ de $\mathcal{E}$ d'images $M'$ tels que le milieu $J$ de $[MM']$ appartient
à la droite $(D)$ d'équations $x=y=z$ est donc le droite d'équations
$$\left\lbrace\begin{array}{rcl} x-z-1 &=& 0 \\ x-y-2 &=& 0\end{array}\right.$$
La relation $(*)$ constitue aussi un système d'équations de notre ensemble !
PROBLÈME. (12 pts)
Partie A
1) a) La fonction $f'''$ étant continue dans l'intervalle fermé borné $I$, est bornée (et atteint
même ses bornes)
Il existe donc un réel $K>0$ tel que pour tout $x\in\;I\;,\ |f'''(x)|\leq K.$
Alors
\begin{eqnarray} \left|\int_{0}^{a}(a-x)^{2}f'''(x)\mathrm{d}x\right| &\leq& \text{signe}(a)\int_{0}^{a}\left|(a-x)^{2} f'''(x)\right|\mathrm{d}x \nonumber \\ &\leq& M.\text{signe}(a)\int_{0}^{a}(a-x)^{2}\mathrm{d}x \nonumber \\ &=& \dfrac{1}{3}M.\text{signe}(a)\left[-(a-x)^{3}\right]_{0}^{a} \nonumber \\ &=& \dfrac{1}{3}M.\text{signe}(a)a^{3} \nonumber \\ &=& \dfrac{1}{3}M|a|^{3} \nonumber \end{eqnarray}
Ensuite $$0\leq\left|\dfrac{1}{a^{2}}\int_{0}^{a}(a-x)^{2}f'''(x)\mathrm{d}x\right|\leq\dfrac{1}{3}M|a|\longrightarrow 0\quad\text{lorsque }a\text{ tend vers }\;0$$
et (Théorème des gendarmes) :$$\lim_{a\rightarrow 0}\dfrac{1}{a^{2}}\int_{0}^{a}(a-x)^{2}f'''(x)\mathrm{d}x=0$$
b) La dérivée de $f''g'-f'g''$ est $$\left(f''g'-f'g''\right)'=f'''g'+f''g''-(f''g''+f'g''')=f'''g'-f'g'''$$
En intégrant cette relation de 0 à $a$ on obtient :
$$\int_{0}^{a}\left(f''g'-f'g''\right)'(x)\mathrm{d}x=\int_{0}^{a}\left(f'''(x)g'(x)-f'(x)g''(x)'\right)\mathrm{d}x$$
c'est à dire la relation demandée
$$\int_{0}^{a}f'(x)g'''(x)\mathrm{d}x=\left[(f'g''-f''g')(x)\right]_{0}^{a}+\int_{0}^{a}f'''(x)g'(x)\mathrm{d}x$$
2) On prend $g(x)=\dfrac{1}{6}(a-x)^{3}$
a) $g'(x)=-\dfrac{1}{2}(a-x)^{2}\;,\ g''(x)=a-x\;,\ g'''(x)=-1$ , et la relation précédente devient : $$-\int_{0}^{a}f'(x)\mathrm{d}x=\left[(f'g''-f''g')(x)\right]_{0}^{a}+\int_{0}^{a}f'''(x)g'(x)\mathrm{d}x$$
En remarquant que $g'$ et $g''$ s'annulent au point $a$ :
$$-(f(a)-f(0))=-(f'(0)g''(0)-f''(0)g'(0))-\dfrac{1}{2}\int_{0}^{a}(a-x)^{2}f'''(x)\mathrm{d}x$$
Il ne reste plus qu'à remplacer $g'(0)$ et $g''(0)$ par leurs valeurs respectives $-\dfrac{1}{2}a^{2}$ et $a$ pour avoir la relation demandée $$f(a)=f(0)+f'(0)a+\dfrac{1}{2}f''(0)a^{2}+\dfrac{1}{2}\int_{0}^{a}(a-x)^{2}f'''(x)\mathrm{d}x$$
b) Appliquons le résultat précédent à la fonction $f$ définie par $f(x)=\mathrm{e}^{x}.$
Toutes les dérivées de $f$ en $x$ sont égales à $\mathrm{e}^{x}$ ; donc toutes les dérivées de $f$ en 0 sont égales à 1.
La relation précédente devient alors :
$$\mathrm{e}^{a}=1+1.a+\dfrac{1}{2}.1.a^{2}+\dfrac{1}{2}\int_{0}^{a}(a-x)^{2}\mathrm{e}^{x}\mathrm{d}x$$
c'est à dire $$\dfrac{\mathrm{e}^{a}-a-1}{a^{2}}=\dfrac{1}{2}+\dfrac{1}{2a^{2}}\int_{0}^{a}(a-x)^{2}\mathrm{e}^{x}\mathrm{d}x$$
et la question 1 permet de conclure, puisque la fonction $x\mapsto \mathrm{e}^{x}$ est bornée dans $[-1\;,\ 1]$ :
$$\lim_{a\rightarrow 0}\dfrac{\mathrm{e}^{a}-a-1}{a^{2}}=\dfrac{1}{2}+\lim_{a\rightarrow 0}\dfrac{1}{2a^{2}}\int_{0}^{a}(a-x)^{2}\mathrm{e}^{x}\mathrm{d}x=\dfrac{1}{2}$$
3) a) $\lim_{t\rightarrow 0}x(t)=\lim_{t\rightarrow 0}\dfrac{t}{\mathrm{e}^{t}-1}=1=x(0)$ , donc la fonction $x$ est continue au point 0.
$\lim_{t\rightarrow 0}y(t)=\lim_{t\rightarrow 0}x(t)\mathrm{e}^{t}=1=y(0)$ , donc la fonction $y$ est continue au point 0.
Regardons le taux d'accroissement $\tau_{1}$ de $x$ au point 0
\begin{eqnarray} \forall\;t\neq 0\;,\ \tau_{1}(t) &=& \dfrac{x(t)-x(0)}{t} \nonumber \\ &=& \dfrac{t-\mathrm{e}^{t}+1}{t(\mathrm{e}^{t}-1)} \nonumber \\ &=& -\dfrac{\mathrm{e}^{t}-t-1}{t^{2}}\dfrac{t}{\mathrm{e}^{t}-1} \nonumber \end{eqnarray}
Le premier facteur de ce dernier membre a pour limite $-\dfrac{1}{2}$ quand $t$ tend vers 0 d'après l'application. Le deuxième facteur a pour limite 1 quand $t$ tend vers 0.
Donc $x$ est dérivable au point 0 et $x'(0)=-\dfrac{1}{2}$
Regardons le taux d'accroissement $\tau_{2}$ de $y$ au point 0
\begin{eqnarray} \forall\;t\neq 0\;,\ \tau_{2}(t) &=& \dfrac{y(t)-y(0)}{t} \nonumber \\ &=& \dfrac{x(t)\mathrm{e}^{t}-1}{t} \nonumber \\ &=& x(t)\dfrac{\mathrm{e}^{t}-1}{t}+\dfrac{x(t)-1}{t} \nonumber \end{eqnarray}
Puisque $x(t)$ a pour limite 1 quand $t$ tend vers 0, $\tau_{2}$ a pour limite $1\times 1-\dfrac{1}{2}=\dfrac{1}{2}$ quand $t$ tend vers 0.
Donc $y$ est dérivable au point 0 et $y'(0)=\dfrac{1}{2}$
b) La tangente $T_{B}$ à $\mathcal{C}$ au point $B(1\;,\ 1)$ est la droite passant par $B$ et de vecteur directeur le vecteur de coordonnées $\left(-\dfrac{1}{2}\;,\ \dfrac{1}{2}\right)$
Partie B
1) a) Pour simplifier, nous allons poser $u_{n}=\mathrm{e}+\dfrac{1}{n}.$
La fonction $f_{1}\ :\ x\mapsto \mathrm{e}^{x}$ est dérivable sur $\mathbb{R}$ et $\forall\;x\in\mathbb{R}\;,\ f_{1}'(x)=\mathrm{e}^{x}$ ; la fonction $f_{2}\ :\ x\mapsto \sqrt{x}$ est dérivable sur $\mathbb{R}_{+}^{*}$ et $\forall\;x\in\mathbb{R}_{+}^{*}\;,\ f_{2}'(x)=\dfrac{1}{2\sqrt{x}}.$
Comme $f$ égale $f_{1}\circ f_{2}-u_{n}.f_{2}$, elle est dérivable sur $\mathbb{R}_{+}^{*}$ et
$$\forall\;x\in\mathbb{R}_{+}^{*}\;,\ f'(x)=f_{1}'(f_{2}(x))f_{2}'(x)-u_{n}.f_{2}'(x)=f_{2}'(x)\left(f_{1}'(f_{2}(x))-u_{n}\right)$$
$\forall\;x\in\mathbb{R}_{+}^{*}\;,\ f'(x)=\dfrac{1}{2\sqrt{x}}\left(\mathrm{e}^{\sqrt{x}}-u_{n}\right)$
Pour étudier la dérivabilité de $f_{n}$ à droite en 0, regardons le taux d'accroissement
\begin{eqnarray} \tau(x) &=& \dfrac{f(x)-f(0)}{x}\;,\quad x>0 \nonumber \\ \tau(x) &=& \dfrac{\mathrm{e}^{\sqrt{x}}-u_{n}\sqrt{x}-1}{x} \nonumber \end{eqnarray}
Posons $a=\sqrt{x}.$ Alors quand $x$ tend vers $0^{+}$, $a$ aussi tend vers $0^{+}$ et
$$\tau(x)=\dfrac{\mathrm{e}^{a}-u_{n}a-1}{a^{2}}=\dfrac{\mathrm{e}^{a}-a-1}{a^{2}}+\dfrac{(1-u_{n})}{a}$$
Dans le dernier membre de cette relation, le premier terme a pour limite $\dfrac{1}{2}$ d'après la partie A ; le deuxième terme a pour limite $-\infty.$ Donc $\lim_{x\rightarrow 0^{+}}\tau(x)=-\infty$
La fonction $f_{n}$ n'est donc pas dérivable au point 0 et de plus au point de $\mathcal{C}_{f_{n}}$ d'abscisse 0 (c'est le point de coordonnées $(0\;,\ 1)$) il y a une demi-tangente verticale.
Remarque 1.
Pour étudier la dérivabilité de $f_{n}$ en 0, on utilise souvent le théorème suivant :
Théorème 1.
Soit $f$ une fonction définie et continue sur un intervalle $I$, dérivable sur $I$ sauf peut-être en un point $a$ de $I.$ Alors
(i) Si $f'$ a une limite $\ell$ quand $x$ tend vers $a$, alors $f$ est dérivable en $a$ et $f'(a)=\ell$
(ii) Si $f'$ a pour limite $+\infty$ ou $-\infty$ quand $x$ tend vers $a$, alors $f$ n'est pas dérivable en $a$ et de plus au point de $\mathcal{C}_{f}$ d'abscisse $a$ il y a une tangente verticale.
Dans le cas présent, $\forall\;x>0\;,\ f'_{n}(x)=\dfrac{1}{2\sqrt{x}}\left(\mathrm{e}^{\sqrt{x}}-u_{n}\right)$ et en posant comme précédemment $a=\sqrt{x}$ , on a :
$$\forall\;x>0\;,\ f'_{n}(x)=\dfrac{1}{2}\dfrac{\mathrm{e}^{a}-u_{n}}{a}=\dfrac{1}{2}\dfrac{\mathrm{e}^{a}-1}{a}+\dfrac{1}{2}\dfrac{1-u_{n}}{a}\longrightarrow "\dfrac{1}{2}-\infty"=-\infty$$
lorsque $a$ tend vers $0^{+}$
b) Au voisinage de $+\infty$, on a une indétermination de la forme $"+\infty-\infty".$ Pour lever cette indétermination écrivons : $ f_{n}(x)=\sqrt{x}\left(\dfrac{\mathrm{e}^{\sqrt{x}}}{\sqrt{x}}-u_{n}\right)$ , puis en posant toujours $a=\sqrt{x}\;,\ f_{n}(x)=a\left(\dfrac{\mathrm{e}^{a}}{a}-u_{n}\right)$
Comme $\lim_{a\rightarrow +\infty}\dfrac{\mathrm{e}^{a}}{a}=+\infty$ , il vient $\lim_{a\rightarrow +\infty}f_{n}(x)=+\infty$
On a aussi $\dfrac{f_{n}(x)}{x}=\left(\dfrac{\mathrm{e}^{a}}{a^{2}}-\dfrac{u_{n}}{a}\right)$ puis $\lim_{x\rightarrow +\infty}\dfrac{f_{n}(x)}{x}=+\infty$
Pour $x>0$ on a :
$$\begin{array}{lclcl} f'_{n}(x)>0 & \Leftrightarrow & \mathrm{e}^{\sqrt{x}}-u_{n} >0 & \Leftrightarrow & \mathrm{e}^{\sqrt{x}}>u_{n} \\ & \Leftrightarrow & \sqrt{x}>\ln u_{n} & \Leftrightarrow & x>(\ln u_{n})^{2}\end{array}$$
Voici le tableau de variations de $f_{n}.$
$$\begin{array}{|c|lrcccr|} \hline x & 0 & \alpha_{n} & 1 & (\ln u_{n})^{2} & \beta_{n} & +\infty \\ \hline f'_{n}(x) & | & & - & | & + & \\ \hline & 1 & \vdots & \vdots & | & \vdots & +\infty \\ & & 0 & \vdots & | & 0 & \\ f_{n} & & & -\frac{1}{n} & | & & \\ & & \searrow & & | & \nearrow & \\ & & & & u_{n}(1-\ln u_{n}) & & \\ & & & & & & \\ \hline\end{array}$$
c) Et voici la courbe $\mathcal{C}_{1}$ et ses tangentes verticale et horizontale.
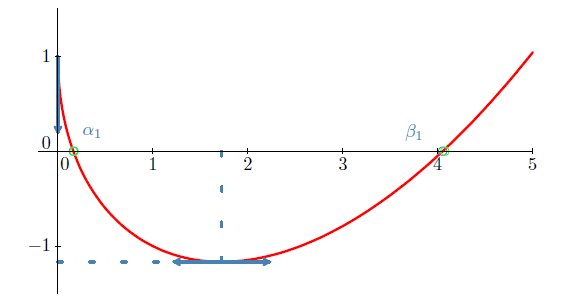
2) a) Puisque un est strictement supérieur à $\mathrm{e}\;,\ \ln u_{n}$ est strictement supérieur 1 ; donc $f((\ln u_{n})^{2})=u_{n}(1-\ln u_{n})$ est strictement négatif.
Comme $f(0)=1$ est strictement positif, d'après le théorème des valeurs intermédiaires, l'équation $f_{n}(x)=0$ admet dans $]0\;,\ (\ln u_{n})^{2}[$ une solution unique $\alpha_{n}.$
De même, $\lim_{x\rightarrow +\infty}f_{n}(x)=+\infty$ permet d'affirmer d'après ce même théorème que l'équation $f_{n}(x)=0$ admet dans $](\ln u_{n})^{2}\;,\ +\infty[$ une solution unique $\beta_{n}.$
$1<(\ln u_{n})^{2}\ $ et $\ f_{n}(1)=-\dfrac{1}{n}<0=f_{n}(\alpha_{n})$ entraîne $\alpha_{n}<1$ car $f_{n}$ est strictement décroissante sur $[1\;,\ (\ln u_{n})^{2}]$
Ainsi on a bien
$$\alpha_{n}<1<(\ln u_{n})^{2}<\beta_{n}$$
b) Pour que la formule d'intégration par parties puisse être appliquée, $v$ doit être tel que
$uv'=\mathrm{e}^{\sqrt{x}}$, ce qui nécessite $v'=\dfrac{\mathrm{e}^{\sqrt{x}}}{\sqrt{x}}$ ou $v'=2\left(\mathrm{e}^{\sqrt{x}}\right)'.$
On peut donc prendre $v=2\mathrm{e}^{\sqrt{x}}.$
La formule donne alors
\begin{eqnarray} \int_{0}^{b}\mathrm{e}^{\sqrt{x}}\mathrm{d}x &=& [uv]_{0}^{b}-\int_{0}^{b}\dfrac{1}{2\sqrt{x}}2\mathrm{e}^{\sqrt{x}}\mathrm{d}x \nonumber \\ &=& [uv]_{0}^{b}-\int_{0}^{b}v'\mathrm{d}x \nonumber \\ &=& [uv-v]_{0}^{b} \nonumber \end{eqnarray}
Finalement $$\int_{0}^{b}\mathrm{e}^{\sqrt{x}}\mathrm{d}x=2+2\mathrm{e}^{\sqrt{b}}(\sqrt{b}-1)$$
c) On a $$\int_{0}^{b}\sqrt{x}\mathrm{d}x=\int_{0}^{b}x^{\frac{1}{2}}\mathrm{d}x=\left[\dfrac{2}{3}x^{\frac{3}{2}}\right]_{0}^{b}=\left[\dfrac{2}{3}x\sqrt{x}\right]_{0}^{b}=\dfrac{2}{3}b\sqrt{b}$$
Par conséquent $$\int_{0}^{b}f(x)\mathrm{d}x=2+2\mathrm{e}^{\sqrt{b}}(\sqrt{b}-1)-\dfrac{2}{3}u_{n}b\sqrt{b}$$
La relation $f_{n}(\alpha_{n})=0$ se traduit par $\mathrm{e}^{\sqrt{\alpha_{n}}}-u_{n}\sqrt{\alpha_{n}}=0$ c'est à dire $\mathrm{e}^{\sqrt{\alpha_{n}}}=u_{n}\sqrt{\alpha_{n}}$
Donc
\begin{eqnarray} I_{n} &=& 2+2\mathrm{e}^{\sqrt{\alpha_{n}}}(\sqrt{\alpha_{n}}-1)-\dfrac{2}{3}u_{n}\alpha_{n}\sqrt{\alpha_{n}} \nonumber \\ &=& 2+2u_{n}{\sqrt{\alpha_{n}}}(\sqrt{\alpha_{n}}-1)-\dfrac{2}{3}u_{n}\alpha_{n}\sqrt{\alpha_{n}} \nonumber \end{eqnarray}
$$I_{n}=2+2u_{n}{\sqrt{\alpha_{n}}}\left(\sqrt{\alpha_{n}}-\dfrac{1}{3}\alpha_{n}-1\right)$$
3) Pour tout $x\in\mathbb{R}_{+}^{*}$ , on pose $\varphi(x)=\dfrac{\mathrm{e}^{x}}{x}$
a) La fonction $\varphi$ est continue et dérivable dans $\mathbb{R}_{+}^{*}$ , et
$$\forall\;x\in\mathbb{R}_{+}^{*}\;,\ \varphi'(x)=\dfrac{x-1}{x^{2}}\mathrm{e}^{x}$$
Le signe de $\varphi'(x)$ est donc celui de $x-1.$
Voici le tableau de variations de $\varphi.$
$$\begin{array}{|c||lcccr|} \hline x & 0 & & 1 & & +\infty \\ \hline \varphi'(x) & & - & | & + & \\ \hline & +\infty & & | & & +\infty \\ \varphi & & \searrow & | & \nearrow & \\ & & & \mathrm{e} & & \\ \hline\end{array}$$
La fonction $\varphi$ est continue et strictement décroissante dans $V_{1}.$ Sa restriction à $V_{1}$ est donc une bijection $h_{1}$ de $V_{1}$ dans $\varphi(V_{1})=W=[\mathrm{e}\;,\ +\infty[.$
La fonction $\varphi$ est continue et strictement croissante dans $V_{2}.$ Sa restriction à $V_{2}$ est donc une bijection $h_{2}$ de $V_{2}$ dans $\varphi(V_{2})=W$
b) La relation $f_{n}(\alpha_{n})=0$ se traduit par $\mathrm{e}^{\sqrt{\alpha_{n}}}-u_{n}\sqrt{\alpha_{n}}=0$ c'est à dire $\dfrac{\mathrm{e}^{\sqrt{\alpha_{n}}}}{\sqrt{\alpha_{n}}}=u_{n}$ ou, puisque $\alpha_{n}$ appartient à $V_{1}\;,\ u_{n}=h_{1}(\alpha_{n}).$
On en déduit, puisque $h_{1}$ est une bijection : $\alpha_{n}=h_{1}^{-1}(u_{n}).$
La fonction $h_{1}$ étant continue et la suite $(u_{n})$ convergente de limite $\mathrm{e}$,
la suite $(\alpha_{n})$ convergente et de limite $h_{1}^{-1}(\mathrm{e})=1$
Sachant que la suite $(\alpha_{n})$ convergente, la relation $I_{n}=2+2u_{n}{\sqrt{\alpha_{n}}}\left(\sqrt{\alpha_{n}}-\dfrac{1}{3}\alpha_{n}-1\right)$ montre que la suite $(I_{n})$ est aussi convergente et de limite $2+2\mathrm{e}.1\left(1-\dfrac{1}{3}-1\right)=2-\dfrac{2}{3}\mathrm{e}$
c) Le même raisonnement montre que la suite $(\beta_{n})$ est convergente et de limite $h_{2}^{-1}(\mathrm{e})=1$
4) a) Les relations $\dfrac{\mathrm{e}^{\sqrt{\alpha_{n}}}}{\sqrt{\alpha_{n}}}=\dfrac{\mathrm{e}^{\sqrt{\beta_{n}}}}{\sqrt{\beta_{n}}}=u_{n}$ montrent que
$\varphi(\sqrt{\alpha_{n}})=\varphi(\sqrt{\beta_{n}})$
c'est à dire , puisque $\sqrt{\alpha_{n}}\in V_{1}$ et $\sqrt{\beta_{n}}\in V_{2}$
$h_{1}(\sqrt{\alpha_{n}})=h_{2}(\sqrt{\beta_{n}})$ ou, $\sqrt{\beta_{n}}=h_{2}^{-1}\circ h_{1}(\sqrt{\alpha_{n}})=h(\sqrt{\alpha_{n}}).$
le point $M_{n}$ appartient bien au graphe de $h.$
b) Soit $x$ un réel
$$x\in\;D_{h}\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} x &\in& D_{h_{1}} \\ h_{1}(x) &\in & D_{h_{2}^{-1}}\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} x &\in& V_{1} \\ h_{1}(x) &\in& V_{2}\end{array}\right.\ \Leftrightarrow\ x \in\;V_{1}$$
Lorsque $x$ tend vers 0, $h_{1}(x)=\varphi(x)$ tend vers $+\infty.$
Lorsque $x$ tend vers $+\infty\;,\ h_{2}^{-1}(x)$ tend vers $+\infty$
donc $$\lim_{x\rightarrow +\infty}h(x)=+\infty$$
Lorsque $x$ tend vers 1, $h_{1}(x)=\varphi(x)$ tend vers $\mathrm{e}.$
Lorsque $x$ tend vers $\mathrm{e}\;,\ h_{2}^{-1}(x)$ tend vers 1
donc $$\lim_{x\rightarrow 1}h(x)=1$$
La fonction h est décroissante car elle la composée de la fonction décroissante $h_{1}$ par la fonction croissante $h_{2}^{-1}.$
c) La fonction $h_{1}$ est dérivable sur $]0\;,\ 1[$ car c'est la restriction de $\varphi$ à $V_{1}.$
La fonction $h_{2}^{-1}$ est dérivable sur $]\mathrm{e}\;,\ +\infty[$ car $h_{2}$ est dérivable sur $V_{2}$ (c'est la restriction
de $\varphi$ à $V_{2}$,) et sa dérivée ne s'annule pas dans $]1\;,\ +\infty[.$
Donc $h=h_{2}^{-1}\circ h_{1}$ est dérivable dans $]0\;,\ 1[.$
Pour tout $x$ appartenant à $V_{1}$ on a
\begin{eqnarray} \varphi[h(x)] &=& h_{2}[h(x)]\quad\text{ car }h(x)\in\;V_{2} \nonumber \\ &=& h_{2}[h_{2}^{-1}\circ h_{1}(x)] \nonumber \\ &=& h_{1}(x) \nonumber \\ &=& \varphi(x)\quad\text{ car }x\in\;V_{1} \nonumber \end{eqnarray}
Remarquons que $\forall\;x\in\mathbb{R}_{+}^{*}\;,\ \varphi'(x)=\dfrac{x-1}{x^{2}}\mathrm{e}^{x}=\dfrac{x-1}{x}\varphi(x).$
En dérivant par rapport à $x$ la relation $\varphi(h(x))=\varphi(x)$, pour $x\in\;]0\;,\ 1[$ on obtient :
$\forall\;x\in\;]0\;,\ 1[\;,\ \varphi'(h(x))h'(x)=\varphi'(x)$ c'est à dire
\begin{eqnarray} \forall\;x\in\;]0\;,\ 1[\;,\ h'(x) &=& \dfrac{\varphi'(x)}{\varphi'(h(x))} \nonumber \\ &=& \dfrac{x-1}{x}\varphi(x)\dfrac{h(x)}{(h(x)-1)\varphi(h(x))} \nonumber \\ &=& \dfrac{x-1}{x}\dfrac{h(x)}{h(x)-1}\quad\text{ car }\varphi(x)=\varphi(h(x)) \nonumber \end{eqnarray}
5) La tangente au point $A$ a pour pente $h'(0\;,\ 4)=\dfrac{0.4-1}{0.4}\dfrac{h(0.4)}{h(0.4)-1}=-3$
Une équation de cette tangente est donc $y=-3(x-0.4)+2$
Finalement $T_{A}\ :\ -3x+3.2$
La tangente $T_{B}$ est déjà déterminée dans la partie A puisque $\mathcal{C}=\mathcal{C}_{h}.$
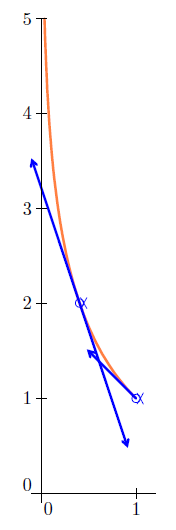

Ajouter un commentaire