Corrigé Bac Maths S2-S2A-S4-S5 1er groupe 2019

 

1) $p_{1}=\dfrac{30}{45}=\dfrac{2}{3}$

 

2) On donne l'arbre de choix pour déterminer les probabilités conditionnelles.

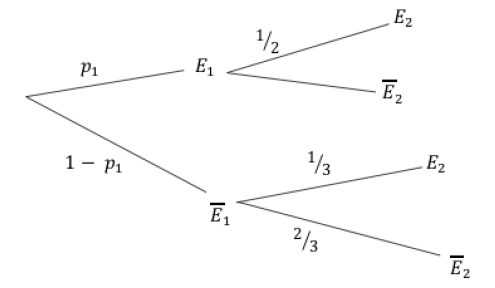
a) $p(E_{2}/E_{1})=\dfrac{1}{2}\ $ et $\ p(E_{2}/\overline{E}_{1})=\dfrac{1}{3}$

 

b) $p(E_{2})=p(E_{2}/E_{1})\times p(E_{1})=\dfrac{1}{2}+p(E_{2}/\overline{E}_{1})\times p(\overline{E}_{1})=\dfrac{4}{9}$

 

3) $E_{n+1}=(E_{n+1}\cap E_{n})\cup(E_{n+1}\cap\overline{E}_{n})$, d'après l'axiome des probabilités totales.

 

D'où : $$p(E_{n+1})=p(E_{n+1}\cap E_{n})+p(E_{n+1}\cap\overline{E}_{n})$$ car $(E_{n+1}\cap E_{n})\ $ et $\ (E_{n+1}\cap\overline{E}_{n})$ sont des événements incompatibles.

 

Donc, $p_{n+1}=p(E_{n+1}/E_{n})\times p_{n}+p(E_{n+1}/\overline{E}_{n})\times p(\overline{E}_{n})$

 

Ce qui donne $p_{n+1}=\dfrac{1}{2}\times p_{n}+\dfrac{1}{3}\times(1-p_{n})$

 

D'où : $$p_{n+1}=\dfrac{1}{6}p_{n}+\dfrac{1}{3}$$

 

4) Soit la suite $(u_{n})$ définie pour tout entier naturel non nul $n$, par : $$u_{n}=p_{n}-\dfrac{2}{5}$$

 

a) 

 

$\begin{array}{rcl} u_{n+1}&=&p_{n+1}-\dfrac{2}{5}\\ \\&=&\dfrac{1}{6}p_{n}+\dfrac{1}{3}-\dfrac{2}{5}\\ \\&=&\dfrac{1}{6}p_{n}-\dfrac{1}{15}\\ \\&=&\dfrac{1}{6}\left(p_{n}-\dfrac{2}{5}\right)\\ \\u_{n+1}&=&\dfrac{1}{6}u_{n}\end{array}$

 

D'où : $(u_{n})_{n\geq 1}$ est une suite géométrique de raison $q=\dfrac{1}{6}$ et de premier terme $u_{1}=\dfrac{4}{15}$

 

b) $u_{n}=u_{1}\left(\dfrac{1}{6}\right)^{n-1}$, 

 

d'où, $u_{n}=\dfrac{4}{15}\left(\dfrac{1}{6}\right)^{n-1}\ $ et $\ u_{n}=\dfrac{4}{15}\left(\dfrac{1}{6}\right)^{n-1}+\dfrac{2}{5}\ $; pour $n\geq 1$

 

c) Ainsi, $\lim_{n\rightarrow +\infty}p_{n}=\dfrac{2}{5}$ car $q=\dfrac{1}{6}<1$

Partie A

 

Pour tout $z\in\mathbb{C}$ on note $f(z)=z^{5}+2z^{4}+2z^{3}-z^{2}-2z-2$

 

1) Déterminons le polynôme $Q$ tel que, $$\forall\;z\in\mathbb{C}\;,\ f(z)=(z^{3}-1)Q(z)$$

 

En faisant la division euclidienne de $f(z)$ par $z^{3}-1$ on trouve que $$Q(z)=z^{2}+2z+2$$

 

2) Résolvons dans $\mathbb{C}$ l'équation $(E)\ :\ f(z)=0$

 

$\begin{array}{rcrcl} f(z)=0&\Leftrightarrow&(z^{3}-1)(z^{2}+2z+2)=0&&\\&\Leftrightarrow&z^{3}-1=0&\text{ou}&z^{2}+2z+2=0\\&\Leftrightarrow&(z-1)(z^{2}+z+1)=0&\text{ou}&z^{2}+2z+2=0\end{array}$

 

Ce qui donne :

 

$z=1\ \text{ ou }\ z=-\dfrac{1-\mathrm{i}\sqrt{3}}{2}\ \text{ ou }\ z=-\dfrac{1+\mathrm{i}\sqrt{3}}{2}\ \text{ ou }\ z=-1-\mathrm{i}\ \text{ ou }\ z=-1+\mathrm{i}$

 

D'où, l'ensemble des solutions de l'équation $f(z)=0$ est : $$S=\left\{1\;;\ -\dfrac{1-\mathrm{i}\sqrt{3}}{2}\;;\ -\dfrac{1+\mathrm{i}\sqrt{3}}{2}\;;\ -1-\mathrm{i}\;;\ -1+\mathrm{i}\right\}$$

 

3) a) Écriture des solutions de $(E)$ sous forme trigonométrique.

 

On pose :

 

$-\ \ z_{0}=1=\cos 0+\mathrm{i}\sin 0\ $ car $arg\;(1)=0\;[2\pi]$

 

$-\ \ z_{1}=-\dfrac{1-\mathrm{i}\sqrt{3}}{2}\;,\ |z_{1}|=1\ $ et $arg\;z_{1}=\dfrac{2\pi}{3}\;[2\pi]$

 

d'où : $z_{1}=\cos\dfrac{2\pi}{3}+\mathrm{i}\sin\dfrac{2\pi}{3}$

 

$-\ \ z_{2}=-\dfrac{1+\mathrm{i}\sqrt{3}}{2}=\overline{z}_{1}\;,\ |z_{2}|=1\ $ et $arg\;z_{2}=-\dfrac{2\pi}{3}\;[2\pi]$

 

d'où : $z_{2}=\cos\dfrac{2\pi}{3}-\mathrm{i}\sin\dfrac{2\pi}{3}$

 

$-\ \ z_{3}=-1+\mathrm{i}\;,\ |z_{3}|=\sqrt{2}\ $ et $arg\;z_{3}=\dfrac{3\pi}{4}\;[2\pi]$

 

d'où : $z_{3}=\cos\dfrac{3\pi}{4}+\mathrm{i}\sin\dfrac{3\pi}{4}$

 

$-\ \ z_{4}=-1-\mathrm{i}=\overline{z}_{3}\;,\ |z_{4}|=\sqrt{2}\ $ et $arg\;z_{4}=-\dfrac{3\pi}{4}\;[2\pi]$

 

d'où : $z_{4}=\cos\dfrac{3\pi}{4}-\mathrm{i}\sin\dfrac{3\pi}{4}$

 

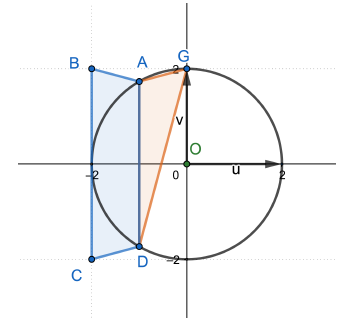
b) Plaçons les points $G\;;\ A\;;\ D\;;\ B\ $ et $\ C$ d'affixes respectives $z_{0}\;;\ z_{1}\;;\ z_{2}\;;\ z_{3}\ $ et $\ z_{4}$ dans le plan complexe $P$ muni d'un repère orthonormale $(O\;;\ \vec{u}\;,\ \vec{v})$

Partie B

 

$z_{\overrightarrow{BC}}=-2\mathrm{i}\ $ et $\ z_{\overrightarrow{AD}}=-\mathrm{i}\ $ d'où $z_{\overrightarrow{BC}}=2z_{\overrightarrow{AD}}$ ce qui implique que $(BC)\ $ et $\ (AD)$ sont parallèles.

 

$z_{\overrightarrow{AB}}=-\dfrac{1}{2}+\mathrm{i}\left(1-\dfrac{\sqrt{3}}{2}\right)\ $ et $\ z_{\overrightarrow{CD}}=\dfrac{1}{2}+\mathrm{i}\left(1-\dfrac{\sqrt{3}}{2}\right)$

 

$\dfrac{z_{\overrightarrow{AB}}}{z_{\overrightarrow{CD}}}$ non réel donc, $(AB)\ $ et $\ (CD)$ sont sécantes.

 

Or $(BC)\ $ et $\ (AD)$ parallèles, et puis $AB=CD$ donc $ABCD$ est un trapèze isocèle.

 

2) $r$ étant une rotation de centre $\Omega$ qui transforme $A\ $ en $\ D.$ On a : $$r(\Omega)=\Omega\quad\text{et}\quad r(A)=D$$

 

Soit $f$ l'application de $\mathbb{C}$ dans $\mathbb{C}$ associée à $r$, alors $$f(z)=az+b\quad\text{avec }\;a\in\mathbb{C}^{*}\setminus\{1\}\;,\ b\in\mathbb{C}\ \text{ et }\ |a|=1$$

 

$r(\Omega)=\Omega$ équivaut à $f(z_{\Omega})=z_{\Omega}\ $ et $\ r(A)=D$ équivaut à $f(z_{A})=z_{D}.$ Ce qui donne : $$\left\lbrace\begin{array}{rcl} z_{\Omega}&=&az_{\Omega}+b\\z_{D}&=&az_{A}+b\end{array}\right.$$

 

$$a=\dfrac{z_{D}-z_{\Omega}}{z_{A}-z\Omega}=\dfrac{1+\mathrm{i}\sqrt{3}}{2}$$

 

$$b=z_{\Omega}-az_{\Omega}=\dfrac{1-\mathrm{i}\sqrt{3}}{2}$$

 

Ce qui donne $$f(z)=\dfrac{1+\mathrm{i}\sqrt{3}}{2}z+\dfrac{1-\mathrm{i}\sqrt{3}}{2}$$

 

3) Nature du triangle $\Omega AD$

 

On sait que $r(A=D$ donc $\Omega A=\Omega D=3\ $, or $AD=|z_{D}-z_{A}|=\sqrt{3}$,

 

d'où triangle $\Omega AD$ est isocèle en $\Omega.$

 

4) Soit $S$ le centre du cercle circonscrit au triangle $\Omega AD.$

 

Puisque le triangle $\Omega AD$ est isocèle en $\Omega$ donc $S$ appartient à la médiatrice du segment $[AD]$ qui est l'axe réel, ce qui implique que $z_{S}$ l'affixe de $S$ est réelle et $SA=SD.$

 

On pose $z_{S}=x\ (x\in\mathbb{R})$ , puisque $S$ est le centre du cercle circonscrit au triangle $\Omega AD$ on a aussi : $$|z_{S}-z_{\Omega}|=|z_{S}-z_{D}|$$

 

Ce qui implique $|x-1|=\left|x+\dfrac{1-\mathrm{i}\sqrt{3}}{2}\right|$

 

d'où : $(x-1)^{2}=\left(x+\dfrac{1}{2}\right)^{2}+\dfrac{3}{4}$

 

ou $x^{2}-2x+1=x^{2}+x+\dfrac{1}{4}+\dfrac{3}{4}$

 

Ce qui donne $x=0.$

 

Donc, $S$ est confondu avec $O$ l'origine du repère d'affixe 0.

 

5) $u_{n}=(z_{A})^{n}\;,\ n\in\mathbb{N}^{*}$ , où $z_{A}$ est l'affixe du point $A.$

 

On sait que $z_{A}=-\dfrac{1}{2}+\mathrm{i}\dfrac{\sqrt{3}}{2}=\mathrm{e}^{\mathrm{i}\frac{2\pi}{3}}$ , d'où $$u_{n}=\mathrm{e}^{\mathrm{i}\frac{2n\pi}{3}}$$

 

$u_{n}$ est réel si, et seulement si, $\sin\dfrac{2\pi n}{3}=0$ , ce qui implique : $$\dfrac{2\pi}{3}n=k\pi\;,\ k\in\mathbb{Z}\;,\ n\in\mathbb{N}^{*}$$ ou $$n=\dfrac{3}{2}k\;,\ k\in\mathbb{Z}\;,\ n\in\mathbb{N}^{*}$$

 

En prenant $k=2$; alors 3 est la valeur minimale de $n$ pour que $u_{n}$ soit un réel.

 

6) La forme algébrique de $u_{2019}$ :

 

$$u_{2019}=\mathrm{e}^{\mathrm{i}\frac{4038\pi}{3}}=\mathrm{e}^{\mathrm{i}1346\pi}$$

 

d'où : $$u_{2019}=1$$

Partie A

 

Soit $g$ la fonction numérique définie pour tout réel $x$ par : $$g(x)=-1+x\mathrm{e}^{\frac{x}{2}}$$

 

1) $\lim_{x\rightarrow +\infty}x\mathrm{e}^{\frac{x}{2}}=+\infty$ ce qui implique que $\lim_{x\rightarrow +\infty}g(x)=+\infty$

 

On sait que $\lim_{X\rightarrow -\infty}X\mathrm{e}^{X}=0$ ce qui implique après un changement de variable que $\lim_{x\rightarrow -\infty}g(x)=-1$

 

2) 

 

$\left\lbrace\begin{array}{l} x\rightarrow\mathrm{e}^{\frac{x}{2}}\ \text{ est définie, continue et dérivable sur }\mathbb{R}\text{ par composée}\\ x\rightarrow x\mathrm{e}^{\frac{x}{2}}\ \text{ est définie, continue et dérivable sur }\mathbb{R}\text{ par produit}\\ \text{d'où }g\ :\ x\rightarrow -1+x\mathrm{e}^{\frac{x}{2}}\ \text{ est définie, continue et dérivable sur }\mathbb{R}\text{ par somme}\end{array}\right.$

 

$\begin{array}{rcl} g'(x)&=&\mathrm{e}^{\frac{x}{2}}+\dfrac{1}{2}x\mathrm{e}^{\frac{x}{2}}\\ \\&=&\mathrm{e}^{\frac{x}{2}}\left(1+\dfrac{1}{2}x\right)\\ \\&=&\dfrac{1}{2}\mathrm{e}^{\frac{x}{2}}(x+2)\end{array}$

 

$$g'(x)=\dfrac{1}{2}\mathrm{e}^{\frac{x}{2}}(x+2)$$

 

$g'(x)$ a le même signe que $x+2$ : 

 

$-\ $ sur $]-\infty\;;\ -2[\;,\ g'(x)<0$

 

$-\ $ sur $]-2\;;\ +\infty[\;,\ g'(x)>0$

 

$-\ $ et $g'(0)=0\ $ si $\ x=-2$

 

$$\begin{array}{|c|lcccr|}\hline x&-\infty&&-2&&+\infty\\ \hline g'(x)&&-&0&+&\\ \hline&-1&&&&+\infty\\ g&&\searrow&&\nearrow&\\&&&-1-\dfrac{2}{\mathrm{e}}&&\\ \hline\end{array}$$

 

3) $g$ est continue et strictement croissante sur $]-2\;;\ +\infty[$, donc $g$ est une bijection de $]-2\;;\ +\infty[$ sur $g(]-2\;;\ +\infty[)=\left]-1-\dfrac{2}{\mathrm{e}}\;;\ +\infty\right[$

 

Or $0\in\left]-1-\dfrac{2}{\mathrm{e}}\;;\ +\infty\right[$, donc l'équation $g(x)=0$ admet une unique solution $\alpha\in]-2\;;\ +\infty[$

 

$g(0.70)\simeq -0.007\ $ et $\ g(0.71)\simeq -0.012$, d'où $g(0.7)\times g(0.71)<0$

 

donc $$\alpha\in]0.70\;;\ 0.71[$$

 

$-\ $ sur $]-\infty\;;\ +\alpha[\;,\ g(x)<0$ ;

 

$-\ $ sur $[\alpha\;;\ +\infty[\;,\ g(x)\geq 0$

 

Partie B

 

1) Soit $f$ la fonction définie pour tout réel $x$ par : $$f(x)=-x+2+(2x-4)\mathrm{e}^{\frac{x}{2}}$$

 

a) 

 

$\left\lbrace\begin{array}{l} x\rightarrow\mathrm{e}^{\frac{x}{2}}\ \text{ est dérivable sur }\mathbb{R}\text{ par composée}\\ x\rightarrow x-2\ \text{ est dérivable sur }\mathbb{R}\\ x\rightarrow(2x-4)\mathrm{e}^{\frac{x}{2}}\ \text{ est dérivable sur }\mathbb{R}\text{ par produit}\\  \text{d'où }f\ :\ x\rightarrow -x+2+(2x-4)\mathrm{e}^{\frac{x}{2}}\ \text{ est dérivable sur }\mathbb{R}\text{ par somme}\end{array}\right.$

 

$\begin{array}{rcl} f'(x)&=&-1+\mathrm{e}^{\frac{x}{2}}\left(2+\dfrac{1}{2}(2x-4)\right)\\ \\&=&-1+\mathrm{e}^{\frac{x}{2}}\left(2+x-2\right)\\ \\&=&-1+x\mathrm{e}^{\frac{x}{2}}\end{array}$

 

d'où $f'(x)=g(x)$ pour tout réel $x.$

 

b) Donc, $f'(x)<0$ sur $]-\infty\;;\ +\alpha[\;;\ f'(x)\geq 0$ sur $[\alpha\;;\ +\infty[$

 

c) On sait que, d'après 3) Partie A, $g(\alpha)=0$ ce qui est équivalent à $\alpha\mathrm{e}^{\frac{\alpha}{2}}$ ou encore $\mathrm{e}^{\frac{\alpha}{2}}=\dfrac{1}{\alpha}$ avec $\alpha\in]0.70\;;\ 0.71[$

 

d'où $f(\alpha)=-\alpha+2+(2\alpha-4)\dfrac{1}{\alpha}$

 

Donc $f(\alpha)=4-\alpha-\dfrac{4}{\alpha}$

 

2) $0.70\leq\alpha\leq 0.71$ 

 

ce qui implique : $4-\dfrac{4}{0.70}-0.71\leq 4-\dfrac{4}{\alpha}-\alpha\leq 4-\dfrac{4}{0.71}-0.70$, d'où $$-2.4\leq f(\alpha)\leq -2.3$$

 

3) a)

 

$\begin{array}{rcl}\lim_{x\rightarrow +\infty}f(x)&=&\lim_{x\rightarrow +\infty}-x+2+(2x-4)\mathrm{e}^{\frac{x}{2}}\\ \\&=&\lim_{x\rightarrow +\infty}(-x+2)\left(1-2\mathrm{e}^{\frac{x}{2}}\right)\\ \\&=&+\infty\end{array}$

 

$\begin{array}{rcl}\lim_{x\rightarrow +\infty}\dfrac{f(x)}{x}&=&\lim_{x\rightarrow +\infty}\left(-1+\dfrac{2}{x}\right)\left(1-2\mathrm{e}^{\frac{x}{2}}\right)\\&=&+\infty\end{array}$

 

b) 

 

$\begin{array}{rcl}\lim_{x\rightarrow -\infty}f(x)&=&\lim_{x\rightarrow -\infty}-x+2+(2x-4)\mathrm{e}^{\frac{x}{2}}\\ \\&=&\lim_{x\rightarrow -\infty}(-x+2)\left(1-2\mathrm{e}^{\frac{x}{2}}\right)\\ \\&=&+\infty\end{array}$

 

4) $\lim_{x\rightarrow -\infty}(f(x)-(-x+2))=\lim_{x\rightarrow -\infty}x\mathrm{e}^{\frac{x}{2}}-4\mathrm{e}^{\frac{x}{2}}=0$

 

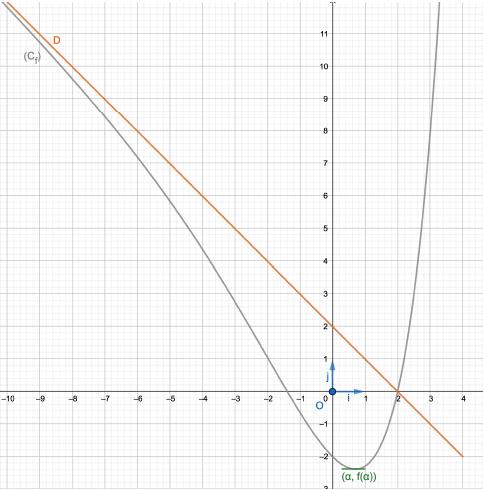
Donc, $(D)\ :\ y=-x+2$ est une asymptote à la courbe $(C_{f})$ au voisinage de $-\infty$

 

5) 

 

$$\begin{array}{|c|lcccr|}\hline x&-\infty&&\alpha&&+\infty\\ \hline f'(x)&&-&0&+&\\ \hline&+\infty&&&&+\infty\\ f&&\searrow&&\nearrow&\\&&&-4-\alpha-\dfrac{4}{\alpha}&&\\ \hline\end{array}$$

 

6)

7) 

 

$\begin{array}{rcl} I(x)&=&\int_{0}^{x}(2t-4)\mathrm{e}^{\frac{t}{2}}\mathrm{d}t\\ \\&=&\left[(4t-16)\mathrm{e}^{\frac{t}{2}}\right]_{0}^{x} \end{array}$

 

d'où $$I(x)=(4x-16)\mathrm{e}^{\frac{x}{2}}+16$$

 

8) 

 

$\begin{array}{rcl} A&=&\int_{\lambda}^{0}\left(-x+2+x-2-(2x-4)\mathrm{e}^{\frac{x}{2}}\right)\mathrm{d}x\times u.a\\ \\&=&\int_{0}^{\lambda}(2x-4)\mathrm{e}^{\frac{x}{2}}\mathrm{d}x\times 4\;cm^{2}\\ \\&=&\left[(4\lambda-16)\mathrm{e}^{\frac{\lambda}{2}}+16\right]\times 4\;cm^{2}\end{array}$

 

$$A=\left[(16\lambda-64)\mathrm{e}^{\frac{\lambda}{2}}+64\right]\;cm^{2}$$

 

$$\lim_{\lambda\rightarrow -\infty}A=\lim_{\lambda\rightarrow -\infty}\left[(16\lambda-64)\mathrm{e}^{\frac{\lambda}{2}}+64\right]\;cm^{2}=64\;cm^{2}$$