Corrigé Bac Physique Chimie 1er groupe S1 S3 2016
Exercice 1
1.1.1 Formules semi-développées :
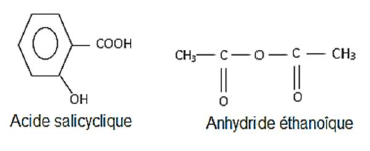
1.1.2 Équation bilan de la réaction :

1.1.3 La réaction est rapide, totale et exothermique : c'est une réaction d'estérification indirecte.
1.2.1 Quantités de matière des réactifs :
$n_{\text{acide}}=\dfrac{3}{18}=2.2\;10^{-2}\;mol$
$n_{\text{anhydre}}=\dfrac{7\times 1.08}{102}=7.4\;10^{-2}\;mol$
L'anhydride est en excès.
1.2.2 Calcul du rendement de la réaction :
$\eta=\dfrac{3.8\times 100}{180\times 2.2\;10^{-2}}=96\%$
Commentaire : la réaction étant totale, le rendement serait sensiblement proche de $100\%.$
La légère différence pourrait relever de la pureté des réactifs utilisés.
1.2.3 Équation de la réaction parasite :
Si l'erlenmeyer n'était pas sec l'anhydride réagirait rapidement avec l'eau suivant la réaction d'équation bilan :
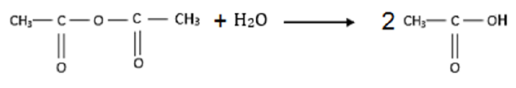
Exercice 2
2.1.1 Équation de la réaction :
$$AH + OH^{-}\ \longrightarrow\ A^{-} + H_{2}0$$
2.1.2 Équivalence acido-basique : lorsque l'acide et les ions hydroxyde sont mélangés dans les proportions stœchiométriques $(n_{AH}=n_{OH^{-}}).$
2.2.1 Établir la relation :
Nombre de mol d'acide présent dans le mélange : $n_{AH(\text{total})}=C_{b}V_{bE}.$
Nombre de mol d'acide ayant réagi avec la base : $n_{AH(\text{réagi})}=C_{b}V_{b}.$
Nombre de mol d'acide restant dans le mélange : $n_{A}=n_{AH(\text{total})}-n_{AH(\text{réagi})}$
On tire que :
$\begin{array}{lrcl}&n_{A}&=&C_{b}V_{bE}-C_{b}V_{b}\\ \Rightarrow&n_{A}&=&C_{b}(V_{bE}-V_{b})\end{array}$
2.2.2 Expression du rapport $\dfrac{[AH]}{[A^{-}]}$
$\begin{array}{lrcl}&\dfrac{[AH]}{[A^{-}]}&=&\dfrac{\dfrac{n_{AH}}{V}}{\dfrac{n_{A^{-}}}{V}}\ =\ \dfrac{C_{b}(V_{bE}-V_{b})}{C_{b}.V_{b}} \\ \\\Rightarrow&\dfrac{[AH]}{[A^{-}]}&=&\dfrac{V_{bE}}{V_{b}}-1\end{array}$
2.2.3 Expression de $[H_{3}O^{+}]$ :
$\begin{array}{lrcl}&K_{a}&=&\dfrac{[H_{3}O^{+}][A^{-}]}{[AH]}\\ \\ \Rightarrow&K_{a}&=&\dfrac{[H_{3}O^{+}]}{\dfrac{V_{bE}}{V_{b}}-1}\\ \\ \Rightarrow&[H_{3}O^{+}]&=&K_{a}\left(\dfrac{V_{bE}}{V_{b}}-1\right)\end{array}$
2.3.1 Tableau de valeur :
$$\begin{array}{|l|c|c|c|c|c|c|c|}\hline V_{b}\;(mL)&2.5&3&3.5&4&4.5&5&5.5\\ \hline pH&3.63&3.74&3.83&3.92&4.01&4.1&4.19\\ \hline [H_{3}O^{+}]\text{ en }10^{-4}\;mol.L^{-1}&2.34&1.82&1.48&1.2&0.98&0.79&0.65\\ \hline \dfrac{1}{V_{b}}\text{ en }mL^{-1}&0.4&0.33&0.29&0.25&0.22&0.2&0.18\\ \hline\end{array}$$
2.3.2 Courbe $[H_{3}O^{+}]=f\left(\dfrac{1}{V_{b}}\right)$
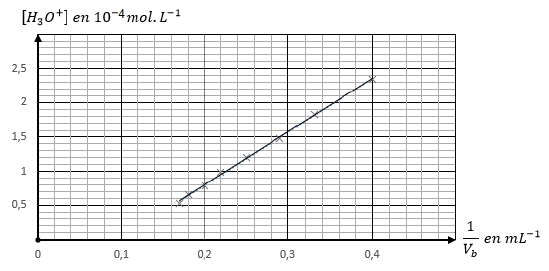
2.3.3 Valeurs du $pK_{a}\ $ et de $\ V_{bE}$ :
Exploitation du graphe donne :
$[H_{3}O^{+}]=7.7\;10^{-4}\times\dfrac{1}{V_{b}}-0.73\;10^{-4}$
De la question 2.2.3 on tire la relation théorique :
$[H_{3}O^{+}]=K_{a}.V_{bE}\dfrac{1}{V_{b}}-K_{a}$
Par identification on tire :
$K_{a}=0.73\;10^{-4}\ \Rightarrow\ pK_{a}=4.1$
$K_{a}.V_{bE}=7.7\;10^{-4}\ \Rightarrow\ V_{bE}\approx 10.5\;mL$
2.4 Masse d'acide dans un comprimé :
$\begin{array}{rcl} m_{AH(\text{total})}&=& n_{AH(\text{total})}.M \\&=&C_{b}.V_{bE}\\ &=&5\;10^{-2}\times 10.5\;10^{-3}\times 5.176\\ &=&0.462\;g \end{array}$
$\boxed{m_{AH(\text{total})}=462\;mg}$
Aux erreurs de mesures près l'indication sur la boîte est proche de la valeur expérimentale donc l'appellation semble correcte.
Exercice 3
3.1.1 Les forces extérieures qui s'appliquent sur $S$ à l'équilibre :
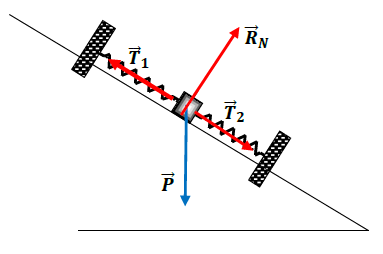
3.1.2 Les allongements $x_{1}\ $ et $\ x_{2}$ à l'équilibre :
$\begin{array}{lrcl}&L&=&(L_{0}+x_{2})+(L_{0}+x_{1}) \\ \Rightarrow&x_{1}+x_{2}&=&L-2L_{0}\end{array}$
T.C.I : $\vec{P}+\vec{R}_{N}+\vec{T}_{1}+\vec{T}_{2}=\vec{0}$
$\begin{array}{lrcl}&-mg\sin\alpha-T_{2}+T_{1}&=&0\\ \Rightarrow&-mg\sin\alpha-kx_{2}+kx_{1}&=&0 \\ \Rightarrow&x_{1}-x_{2}&=&\dfrac{mg\sin\alpha}{k}\end{array}$
Ainsi, $x_{1}=\dfrac{1}{2}\left(L-2L_{0}+\dfrac{mg\sin\alpha}{k}\right)\ $ et $\ x_{2}=\dfrac{1}{2}\left(L-2L_{0}-\dfrac{mg\sin\alpha}{k}\right)$
A.N : $x_{1}=6.25\;cm\ $ et $\ x_{2}=3.75\;cm$
3.2.1 Équation différentielle du mouvement :
T.C.I : $\vec{P}+\vec{R}_{N}+\vec{T}_{1}'+\vec{T}_{2}'=m\vec{a}$
En projetant sur l'axe $xx'$ parallèle au plan et orienté vers le haut on obtient :
$k(x_{1}-x)-k(x_{2}+x)+mg\sin\alpha=m\ddot{x}$
Or $\ mg\sin\alpha+kx_{2}-kx_{1}=0$
On tire : $$\ddot{x}+\dfrac{2k}{m}x=0$$
3.2.2 Nature du mouvement : l'équation différentielle montre que le système étudié un oscillateur harmonique : le mouvement est rectiligne sinusoïdal.
Expression de $T_{0}$ : $$T_{0}=2\pi\sqrt{\dfrac{m}{2k}}$$
3.3 Montrons que : $\ddot{x}+\dfrac{2k}{m}x=0$
Système conservatif, l'énergie mécanique est constante ; $\dfrac{dE_{m}}{dt}=0$
$E_{m}=E_{c}+E_{p}\ $ or $\ E_{c}=\dfrac{1}{2}\dot{x}^{2}\ $ et $\ E_{p}=\dfrac{1}{2}k(x_{2}+x)^{2}+\dfrac{1}{2}k(x_{1}-x)^{2}+mgx\sin\alpha$
donc, $E_{m}=\dfrac{1}{2}\dot{x}^{2}+\dfrac{1}{2}k(x_{2}+x)^{2}+\dfrac{1}{2}k(x_{1}-x)^{2}+mgx\sin\alpha$
$\Rightarrow\ \dfrac{dE_{m}}{dt}=m\dot{x}\ddot{x}+k\dot{x}(x_{2}+x)-k\dot{x}(x_{1}-x)+mg\dot{x}\sin\alpha$
$\Rightarrow\ \dot{x}[k(x_{2}-x_{1}+2x)+mg\sin\alpha+m\ddot{x}]=0$
Or $\ mg\sin\alpha+kx_{2}-kx_{1}=0$
On tire : $$\ddot{x}+\dfrac{2k}{m}x=0$$
3.4.1 Identification
Au passage par $x$ la vitesse est maximale donc l'énergie cinétique est maximale :
$C_{1}$ correspond à $E_{c}.$
Au passage par $x$ l'énergie potentielle est nulle : $C_{2}$ correspond à $E_{p}.$
L'élongation étant la seule grandeur algébrique parmi les trois donc $C_{3}$ correspond à $x.$
3.4.2 Valeurs des périodes :
Période pour $E_{p}\ $ ou $\ E_{c}\ :\ T=47\times 3=141\;ms.$
Période pour $x\ :\ T_{0}=47\times 6=282\;ms.$
Comparaison : $T_{0}=2T$
3.5 Valeur de chaque division :
$\begin{array}{rcl}E_{p}=\dfrac{1}{2}k(x_{1}^{2}+x_{2}^{2})&=&\dfrac{1}{2}.20.((6.25)^{2}+(3.75)^{2}).10^{-4}\\&=&53.125\;10^{-3}\;J\\\Rightarrow\ E_{p}/\text{division}&=&\dfrac{E_{p}}{3}\\&=&17.7\;mJ\ \text{ par division}\end{array}$
Déduction de la vitesse maximale :
$E_{C\text{ max}}=\dfrac{1}{2}mV_{\text{max}}^{2}\ \Rightarrow\ V_{\text{max}}=\sqrt{\dfrac{2.E_{C\text{ max}}}{m}}$
Or, d'après graphe $E_{C\text{ max}}=3\text{ divisions }=53.125\;10^{-3}\;J$
Donc, $V_{\text{max}}=\sqrt{\dfrac{2\times 53.125\;10^{-3}}{0.1}}=1.0\;m/s$
Exercice 4
4.1.1 Expression de la vitesse :
T.E.C entre $P_{1}\ $ et $\ P_{2}$ :
$\begin{array}{lrcl}&\dfrac{1}{2}mV^{2}-0&=&W_{P_{1}\rightarrow P_{2}}^{\vec{F}}\\& &=&qU\\ \Rightarrow&V&=&\sqrt{\dfrac{2.qU}{m}}\end{array}$
4.1.2 Nature de la portion du trajet $(E\;,\ S)$ :
$\begin{array}{rcrcrcl}\vec{F}_{m}&=&m.\vec{a}&\Rightarrow&\vec{a}&=&\dfrac{q}{m}.\vec{V}\wedge\vec{B}\\ \\ & & &\Rightarrow&\vec{a}&\perp&\vec{V}\\ \\ & & &\Rightarrow&a_{t}&=&0\\ \\ & & &\Rightarrow&\dfrac{dV}{dt}&=&0\\ \\ & & &\Rightarrow&V&=&cste\end{array}$
$\begin{array}{rcrcrcl}\vec{a}&=&\dfrac{q}{m}.\vec{V}\wedge\vec{B}&\Rightarrow&a_{t}&=&0\\ \\ & & &\Rightarrow&\vec{a}&=&\vec{a}_{N}\end{array}$
Comme $a=\dfrac{|q|.VB}{m}\ $ et $\ a_{N}=\dfrac{V^{2}}{\rho}$ alors, $\rho=\dfrac{m.V}{|q|.B}=cste$
$(ES)\ $ est un arc de cercle de rayon $R=\dfrac{m.V}{|q|.B}$
4.1.3 Expression de la durée $\tau$ :
$\begin{array}{rcrcrcl}\widehat{ES}\ =\ R.\beta&=&\tau.V&\Rightarrow&\tau&=&\dfrac{\beta.R}{V}\ =\ \dfrac{\beta.m.V}{V.q.B}\\& & &\Rightarrow&\tau&=&\dfrac{m.\beta}{q.B}\end{array}$
4.2.1 Valeur du rayon de la trajectoire pour $_{1}^{1}H^{+}$
$\begin{array}{lrcl}&R&=&\dfrac{m.V}{|q|.B}\quad\text{or }\ V=\sqrt{\dfrac{2.qU}{m}}\\ \\\Rightarrow&R&=&\dfrac{1}{B}.\sqrt{\dfrac{2.m.U}{q}}\\ \\& &=&\dfrac{1}{0.5}.\sqrt{\dfrac{2\;10^{-3}\times8025}{6.02\;10^{23}\times 1.6\;10^{-19}}}\\ \\& &=&2.58\;cm\ \approx\ 2.6\;cm\end{array}$
4.2.1 Valeurs des autres nombre de masse :
$\begin{array}{lrcl}&R^{2}&=&\dfrac{2.m_{1}.U_{1}}{q.B^{2}}\ =\ \dfrac{2.A_{1}.u.U_{1}}{q.B^{2}}\\ \\\Rightarrow&A_{1}&=&\dfrac{R^{2}.q.B^{2}}{2.u.U_{1}}\\ \\& &=&\dfrac{(0.0258)^{2}\times 1.6\;10^{-19}\times(0.5)^{2}}{2\times 1.66\;10^{-27}\times 2675}\\ \\& &=&3\end{array}$
Ainsi, $A_{1}=3\ $ et $\ A_{2}=2$
4.3 Expression de $D=FC$ :
$\sin\dfrac{\beta}{2}=\dfrac{R}{OF}=\dfrac{R}{OC}$ ;
$\left\lbrace\begin{array}{rcl}\cos\beta&=&\cos^{2}\left(\dfrac{\beta}{2}\right)-\sin^{2}\left(\dfrac{\beta}{2}\right)\\ \\1&=&\cos^{2}\left(\dfrac{\beta}{2}\right)+\sin^{2}\left(\dfrac{\beta}{2}\right)\end{array}\right\rbrace\ \Rightarrow\ 1-\cos\beta\ =\ 2\sin^{2}\left(\dfrac{\beta}{2}\right)$
$D=OF+OC=2OF\ $ or $\ OF=\dfrac{R}{\sin\dfrac{\beta}{2}}=\dfrac{D}{2}$
Donc, $\sin\dfrac{\beta}{2}=\dfrac{2R}{D}$
On tire : $\sin^{2}\left(\dfrac{\beta}{2}\right)=\left(\dfrac{2R}{D}\right)^{2}$
$1-\cos\beta=2\times\left[\dfrac{2R}{D}\right]^{2}=\dfrac{8R^{2}}{D^{2}}\ $ or $\ R=\dfrac{1}{B}.\sqrt{\dfrac{2.m.U}{q}}$
On tire : $D=\dfrac{4}{B}.\sqrt{\dfrac{m.U}{q(1-\cos\beta)}}$
4.4.1 Valeur de $R'$ :
$R'=\dfrac{m.V_{c}}{|q|.B}=\dfrac{1.66\;10^{-27}\times 1.24\;10^{6}}{1.6\;10^{-19}\times 0.5}=2.573\;cm$
4.4.2 Expressions des vitesses :
Conservation de la quantité de mouvement :
$m_{p}\vec{V}_{c}=m_{p}\vec{V}_{p'}+m_{n}\vec{V}_{n'}\ \Rightarrow\ m_{n}\vec{V}_{n'}=m_{p}(\vec{V}_{c}-\vec{V}_{p'})$
Conservation énergie cinétique :
$\dfrac{1}{2}mV_{c}^{2}=\dfrac{1}{2}mV_{p'}^{2}+\dfrac{1}{2}mV_{n'}^{2}\ \Rightarrow\ \vec{V}_{c}+\vec{V}_{p'}=\vec{V}_{n'}$
On tire : $\left\lbrace\begin{array}{rcl} V_{p'}&=&\left|V_{c}\left(\dfrac{m_{p}-m_{n}}{m_{p}+m_{n}}\right)\right|\\ \\V_{n'}&=&2V_{c}\dfrac{m_{p}}{m_{p}+m_{n}}\end{array}\right.$
4.4.3 Détermination de $m_{n}$ :
Par exploitation des rayon des trajectoires
$\left(R_{p}=2.5\;cm\;;\ R_{n'}=\dfrac{10}{3}\;cm\quad\text{et}\quad R_{p'}=\dfrac{5}{3}\;cm\right)$
On trouve $m_{n}=2m_{p}\ $; c'est $\ _{1}^{2}H^{+}$
4.5.1 Équation de la trajectoire : mouvement (voir cours).
4.5.2 Montrer que $E=\dfrac{m_{p}V_{c}^{2}}{18qR_{p'}}$
Exercice 5
5.1 Équation de la réaction : $$_{53}^{131}I\ \longrightarrow\ _{54}^{131}Xe\ +\ _{-1}^{\;\ 0}e\ +\ _{0}^{0}\overline{v}$$
La radioactivité est de type $\beta^{-}$
5.2 L'intérêt de la mesure : la prise des comprimés d'iode 127 (non radioactifs) permet une saturation du corps en iode Cette saturation empêche la fixation de l'iode 131 (radioactif) ce qui procure une protection.
5.3 Définition : l'activité radioactive est le nombre de désintégration par unité de temps.
Dans le S.I elle s'exprime en becquerel $(Bq)$
$\begin{array}{rcl} A\ =\ \lambda.N&=&\dfrac{\ln 2}{T}.\dfrac{m}{M}.\mathcal{N}\\ \\ &=&\dfrac{0.69\times 1\times 6.02\;10^{23}}{8.1\times 24\times 3600\times 131}\\ \\&=&4.6\;10^{15}\;Bq\end{array}$
$A_{0}=37\;10^{6}\;Bq$
5.4 Masse m' d'iode à injecter :
$\begin{array}{rcrcrcl}\dfrac{m_{0}}{m}&=&\dfrac{A_{0}}{A}&\Rightarrow&m_{0}&=&\dfrac{A_{0}}{A}.m\\ \\& & & & &=&\dfrac{37\;10^{6}\times 1}{4.6\;10^{15}}\\ \\& & & & &=&8\;10^{-9}\;g\end{array}$
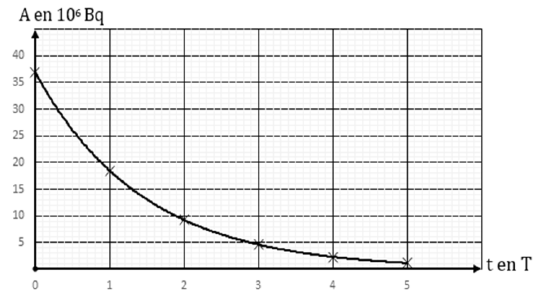
5.5 Courbe de décroissance :
$$\begin{array}{|l|c|c|c|c|c|c|}\hline t\text{ en } T&0&1&2&3&4&5\\ \hline A\text{ en } 10^{6}\;Bq&37&18.5&9.25&4.63&2.31&1.16\\ \hline\end{array}$$

Ajouter un commentaire