On donne les réels $m = 1 - 2\sqrt{3}$,  $p =\sqrt{13 - 4\sqrt{3}}$ et $q =\sqrt{13 + 4\sqrt{3}}$

 

1) Montre que $m$ est négatif (1 pt)
 

2) Calcule $m^2$ puis déduis-en que p et m sont opposés            (0,5 pt + 0,5 pt)

 

3) Encadre $m$ à $10^{-2}$ près sachant que $1,732 <\sqrt{3}< 1,733$            (1,5 pts)

 

4) Montre que : $p \times q = 11$.                            (1,5 pts)

Les lutteurs d'une écurie sont répartis en cinq classes de poids (catégories de poids) d'amplitude $15\;kg.$

 

On a les classes suivantes : $[80\;;\ 95[$, $[95\;;\ 110[$, $[110 \;;\ 125[$, $[125 \;;\ 140[\ $ et $\ [140\; ;\ 155[.$

 

1) Les lutteurs de la classe $[95\;;\ 110[$ sont au nombre de $6$ et représentent $12\%$ de l'effectif de l'écurie.

 

Montre qu'il y a $50$ lutteurs dans cette écurie.                (0,5 pt)

 

2) L'angle de la représentation de la classe $[110\;;\ 125[$ dans le diagramme circulaire de la série est $36°$

 

Montre que le nombre de lutteurs de cette classe est $5$.            (1 pts)

 

3) La fréquence de la classe $[125\;;\ 140[$ est $0.3$. Vérifie que cette classe compte $15$ lutteurs.    (0,5 pt)

 

4) L'effectif de la classe $[140 ; 155[$ est le tiers de l'effectif de la classe $[80\;;\ 95[.$

 

Montre qu'il y a $6$ lutteurs dans la classe $[140\;;\ 155[$.            (1,5 pts)

 

5) Etablis le tableau des effectifs cumulés croissants de cette série puis déduis-en la classe médiane.                        (1 pt + 0.5 pt)

Dans le plan muni d'un repère orthonormal $\left(O, \vec{i}, \vec{j}\right)$, on considère les droites $$(D_1): y= - x + 1\quad\text{ et }\quad(D_2) : x - y + 3 = 0$$

1) Démontre que les droites $(D_1)$ et $(D_2)$ sont perpendiculaires.        (0,5 pt)

2) a) Construis les droites $(D_1)$ et $(D_2)$                    (0,5pt + 0,5pt)

b) Justifie par le calcul que le point $J$ appartient à la droite (D$_1$)     (0,5 pt)

c) On appelle $E$ le point d'intersection de $(D_1)$ et $(D_2)$. Justifie par le calcul que E a pour couple de coordonnées (-1; 2). (1 pt)

d) Calcule la distance $EJ$ (0,5 pt)

e) Détermine une équation de la droite $(D_3)$  passant par $J$ et parallèle à $(D_2)$. (1 pt)

f) Quelle est la position relative de $(D_3)$ et $(D_1)$? Justifie ta réponse.    (0,5 pt)

On considère la figure codée ci-dessous :

 

 

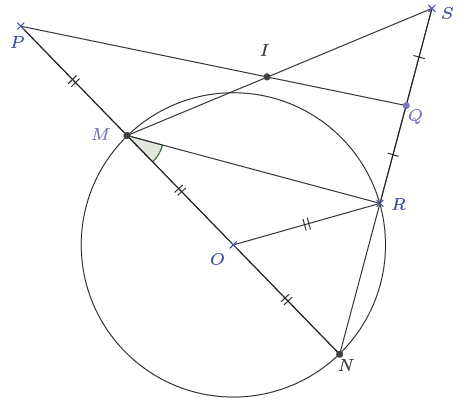
1) Justifie que le triangle $NRM$ est rectangle. (0,5 pt)

 

Dans toute la suite du problème on suppose que $MR = 8\ cm$ et $NR = 6\ cm$

 

2) Calcule $MN$    (1 pt)

 

3) Calcule $tan \widehat{RMN}$ ? (0,5 pt)

 

4) Démontre que $I$ est le milieu de $[MS]$. (1 pt)

 

5) Montre que $NQ =  9\ cm$        (1 pt)

 

6) Démontre que la droite $(OR) $est parallèle à la droite $(MS)$. (1 pt)