BFEM Physique chimie 2010
Exercice 1 (4 points)
Un briquet neuf rempli de gaz butane $(C_{4}H_{10})$ a une masse de $14.8\;g.$ Utilisé pendant quelques jours, le briquet est vidé de son contenu ; sa masse est alors $9\;g.$ Tout le butane a réagi avec le dioxygène de l'air et la combustion est supposée complète.
2.1 Écrire l'équation-bilan de la combustion complète du butane. $\quad(01\;pt)$
2.2 Calculer la quantité de matière (nombre de mol) de butane brûlée. $\quad(01\;pt)$
2.3 En déduire le volume de dioxygène nécessaire à cette combustion. $\quad(01\;pt)$
2.4 Calculer la quantité de chaleur libérée sachant que la combustion d'une mole de gaz butane libère une quantité de chaleur de $2800\;kJ.\quad(01\;pt)$
On donne :
Volume molaire $V_{m}=24 L.mol^{-1}\;;\ M(C)= 12\;g.mol^{-1}\;;\ M(H)=1\;g.mol^{-1}$
Exercice 2 (4 points)
On dispose d'une solution d'acide chlorhydrique $(H^{+}+Cl^{-})$ de concentration molaire $C_{a}$ inconnue.
1.1 On prélève quelques millilitres de la solution que l'on introduit dans un tube à essais contenant de la grenaille de zinc. Il se produit une réaction chimique et on observe un dégagement gazeux. En approchant une flamme au dessus de l'ouverture du tube, on entend une petite explosion.
1.1.1 Quel est le nom du gaz qui se dégage ? Quelle est sa formule chimique ? $\quad(01\;pt)$
1.1.2 Sachant qu'il se forme aussi des ions $Zn^{2^{+}}$, écrire l'équation-bilan de la réaction entre les ions $H^{+}$ et les atomes de zinc. $\quad(01\;pt)$
1.2 On prélève à nouveau $10\;mL$ de la solution d'acide que l'on met dans un bêcher, on y ajoute quelques gouttes de bleu de bromothymol $(BBT).$ On dose alors l'acide par une solution d'hydroxyde de sodium $(Na^{+}+OH^{-})$ de concentration molaire $C_{b} = 5.10^{-2}\;mol.L^{-1}$. Le volume de base versé à l'équivalence est $V_{b}=20\;mL.$
1.2.1 Quelle observation expérimentale permet d'affirmer que l'équivalence est atteinte ? $\quad(01\;pt)$
1.2.2 Déterminer la concentration $C_{a}$ de la solution d'acide. $\quad(01\;pt)$
Exercice 3 (6 points)
On a mesuré la résistance de deux fils cylindriques, de même section $S$, mais de métaux différents. Les résultats obtenus sont regroupés dans le tableau ci-après.
$$\begin{array}{|c|c|c|}\hline\text{Métal}&\text{Longueur du fil en }(m)&\text{Résistance du fil en }(\Omega)\\ \hline\text{Aluminium}&10&7.8\\ \hline\text{Cuivre}&50&25\\ \hline\end{array}$$
3.1 Calculer pour chaque fil la résistance pour une longueur de $100\;m.\quad(02\;pt)$
3.2 Lequel des métaux est meilleur conducteur électrique ? Justifier la réponse. $\quad(02\;pt)$
3.3 La résistivité du cuivre vaut $\rho=1.8\;10^{-8}\;\Omega.m$. En déduire la valeur de la section S des fils. $\quad(02\;pt)$
Exercice 4 (6 points)
4.1 L'objectif de l'appareil sera assimilé à une lentille convergente de distance focale $50\;mm.$ Calculer la vergence de cette lentille. $\quad(01\;pt)$
4.2 L'arbre AB étant situé à une distance $D$ de l'objectif de l'appareil, l'image $A'B'$, de hauteur $h$, se forme à la distance $d$ du centre optique de la lentille comme indiqué sur le schéma ci-contre.
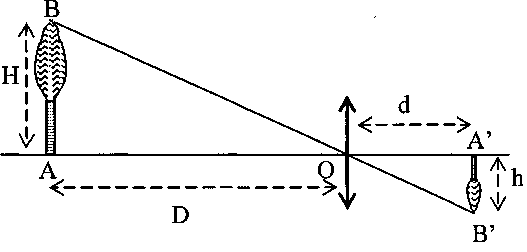
4.2.1 Donner les caractéristiques de l'image $\quad(02\;pt)$
4.2.2 Le groupe d'élèves calcule la hauteur de l'arbre à partir de la relation : $H=\dfrac{Dh}{d}$.
a) Retrouver cette relation à partir du schéma. $\quad(01.5\;pt)$
b) Calculer la hauteur de l'arbre avec les données suivantes :
$D=10\;m\;;\ d=50.2\;mm\ $ et $\ h=1.5\;cm.\quad(01.5\;pt)$
NB : les distances ne sont pas respectées sur le schéma.
