Bac maths, C. étrangers

 

5 points

 

Soit $ABCD$ un tétraèdre tel que $ABC\;,\ ABD$ et $ACD$ soient trois triangles isocèles rectangles en A avec $AB=AC=AD=a$. On appelle $A_{1}$ le centre de gravité du  triangle $BCD.$

 

1. Montrer que la droite $(AA_{1})$ est orthogonale au plan $(BCD)$ (on pourra par exemple calculer $\overrightarrow{AA_{1}}\cdot\overrightarrow{CD}$ et $\overrightarrow{AA_{1}}\cdot\overrightarrow{BC}$)

 

2. En exprimant de deux façons différentes le volume du tétraèdre $ABCD$, calculer la longueur du segment $[AA_{1}].$

 

3. On appelle $G$ l'isobarycentre du tétraèdre $ABCD$ et $I$ le milieu de $[BC].$

 

a. Montrer que $G$ appartient au segment $[AA_{1}]$ et déterminer la longueur $AG.$

 

b. Déterminer l'ensemble des points $M$ de l'espace tels que $$||\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}||=2||\overrightarrow{MB}+\overrightarrow{MC}||$$

 

4. Soit $H$ le symétrique de $A$ par rapport à $G$.

 

a. Démontrer que $$4\vec{GA}+\overrightarrow{AC}+\overrightarrow{AD}=\overrightarrow{BA}$$

 

b. Démontrer l'égalité $$HC^{2}-HD^{2}=\overrightarrow{DC}\cdot\overrightarrow{BA}$$

 

c. En déduire que $HC=HD$.

 

On rappelle que le volume d'une pyramide de hauteur $h$ et d'aire de base $b$ est $V=\dfrac{1}{3}hb.$

Attention à bien lire l'énoncé...

 

Soit $ABCD$ un tétraèdre tel que $ABC\;,\ ABD$ et $ACD$ soient trois triangles isocèles rectangles en $A$ avec $AB=AC=AD=a.$ On appelle $A_{1}$ le centre de gravité du triangle $BCD.$

 

1. $(AA_{1})$ est dans le plan médiateur de $[BC]$ puisque $AB=AC\;;\ $ ($ABC$ isocèle) et $A_{1}B=A_{1}C\;;\ $ ($BCD$ équilatéral), $(BC)$ est donc orthogonale à toutes les directions de ce plan, particulièrement à $(AA_{1}).$

 

Le calcul des produits scalaires n'est pas nécessaire et en plus risque d'embrouiller l'esprit...

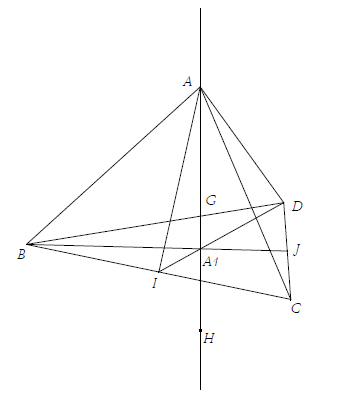
2. D'un côté on a $BC=a\sqrt{2}\;,\quad DI=BC\dfrac{\sqrt{3}}{2}=a\dfrac{\sqrt{6}}{2}$

d'où :

\begin{eqnarray} V&=&\dfrac{1}{3}(BCD).AA_{1} \nonumber \\ &=&\dfrac{1}{3}\left(\dfrac{1}{2}a\sqrt{2}\dfrac{\sqrt{3}}{2}a\sqrt{2}\right)AA_{1} \nonumber \\ &=&\dfrac{a^{2}\sqrt{6}}{6}AA_{1} \nonumber \end{eqnarray}

 

d'un autre côté on a $(DA)$ orthogonal à $(AB)$ et $(AC)$, donc $(DA)$ orthogonal à $(ABC)$, soit \begin{eqnarray} V&=&aire(ABC).DA \nonumber \\ &=&\dfrac{1}{3}\left(\dfrac{1}{2}a^{2}\right)a \nonumber \\ &=&\dfrac{1}{6}a^{3} \nonumber \end{eqnarray} 

on en déduit $$AA_{1}=\dfrac{1}{6}a^{2}\dfrac{6}{a^{2}\sqrt{6}}=\dfrac{a}{\sqrt{6}}$$

 

3. a. $G$ = barycentre de $\{(A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1)\;,\ (D\;,\ 1)\}$ ou encore de $\{(A\;,\ 1)\;,\ (A_{1}\;,\ 3)\}$ , on a donc $\overrightarrow{AG}=\dfrac{3}{4}\overrightarrow{AA_{1}}.$

 

Donc $G$ appartient au segment $[AA_{1}]$ et $AG=\dfrac{3}{4}AA_{1}=\dfrac{3a}{4\sqrt{6}}.$

 

b. On introduit $G$ dans le vecteur de gauche, $I$ dans celui de droite, et on a \begin{eqnarray} ||4\overrightarrow{MG}||&=&2||\overrightarrow{MI}|| \nonumber \\ \Leftrightarrow\ MG&=&MI \nonumber \end{eqnarray}

 

L'ensemble cherché est le plan médiateur de $[GI].$

 

4. a. On met $G$ partout et on utilise $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\vec{0}$ :

$$4\overrightarrow{GA}+\overrightarrow{AG}+\overrightarrow{GC}+\overrightarrow{AG}+\overrightarrow{GD}=\overrightarrow{BG}+\overrightarrow{GA}\ \Leftrightarrow\ \overrightarrow{GA}+\overrightarrow{GC}+\overrightarrow{GD}+\overrightarrow{BG}=\vec{0}$$

 

b. On factorise : \begin{eqnarray} HC^{2}-HD^{2}&=&(\overrightarrow{HC}-\overrightarrow{HD})(\overrightarrow{HC}+\overrightarrow{HD}) \nonumber \\ &=&\overrightarrow{DC}\cdot 2\overrightarrow{HJ} \nonumber \\ &=&\overrightarrow{DC}\cdot\overrightarrow{BA}\quad (\text{Thalès dans }ABHJ) \nonumber \end{eqnarray} 

 

c. Comme $(DC)$ est orthogonal à $(AB)$, on a $HC^{2}=HD^{2}\ \Rightarrow\ HC=HD.$