Bac maths, France

 

3 points

 

 

L'espace est muni du repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}).$

 

Soient $(P)\ $ et $\ (P')$ les plans d'équations respectives $$x+2y-z+1=0\quad\text{et}\quad -x+y+z=0$$ 

 

Soit $A$ le point de coordonnées $(0\;;\ 1\;;\ 1).$

 

1. Démontrer que les plans $(P)\ $ et $\ (P')$ sont perpendiculaires.

 

2. Soit $(d)$ la droite dont une représentation paramétrique est : $$\left\lbrace\begin{array}{lll} x &=& -\dfrac{1}{3}+t\\ y &=& -\dfrac{1}{3} \\ z &=& t \end{array} \right.\;,\quad \text{où }t\text{ est un nombre réel}$$

 

Démontrer que les plans $(P)\ $ et $\ (P')$ se coupent selon la droite $(d).$

 

3. Calculer la distance du point $A$ à chacun des plans $(P)\ $ et $\ (P').$

 

4. En déduire la distance du point $A$ à la droite $(d).$

1. $\vec{n}_{_{P}}\begin{pmatrix} 1\\ 2\\ -1 \end{pmatrix}\;,\ \vec{n}_{_{P'}}\begin{pmatrix} -1\\ 1\\ 1 \end{pmatrix}$ 

 

$\vec{n}_{_{P}}\cdot\vec{n}_{_{P'}}=-1+2-1=0$  donc les plans $(P)$ et $(P')$ sont perpendiculaires.

 

2.

 

$\begin{array}{rcl} \left\lbrace\begin{array}{rcl} x+2y-z+1 &=& 0\\ -x+y+z &=& 0\\ z &=& t \end{array} \right.&\Leftrightarrow&\left\lbrace\begin{array}{lcl} x+2y &=& t-1\\ -x+y &=& -t\\ z &=& t \end{array} \right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x &=& \dfrac{2}{3}+t-1\\ \\ y &=& -\dfrac{1}{3}\\ \\ z &=& t \end{array} \right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{lcl} x &=& t-\dfrac{1}{3}\\ \\ y &=& -\dfrac{1}{3}\\ \\ z &=& t \end{array} \right. \end{array}$ 

 

3.

 

$\begin{array}{rcl} d(A\;;\ P)&=&\dfrac{|0+2-1+1|}{\sqrt{1+4+1}} \\ \\ &=&\dfrac{2}{\sqrt{6}}=2\sqrt{3}\end{array}$

 

$\begin{array}{rcl} d(A\;;\ P')&=&\dfrac{|0+1+1|}{\sqrt{1+1+1}} \\ \\ &=&\dfrac{2}{\sqrt{3}}\end{array}$

 

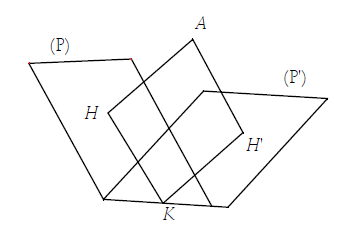
4. Soit $H\ $ et $\ H'$ les projections orthogonales de $A$ sur les plans ; $K$ le point d'intersection entre le plan $(AHH')\ $ et $\ (d)$ ; la distance de $A$ à $(d)$ est $AK.$

 

Par ailleurs, les deux plans sont orthogonaux, $AHKH'$ est donc un rectangle, soit :

 

$\begin{array}{rcl} AK^{2}&=&AH^{2}+AH'^{2} \\ \\ &=&\dfrac{4}{6}+\dfrac{4}{3} \\ \\ &=&\dfrac{12}{6}=2 \\ \\ \Rightarrow\ AK&=&\sqrt{2}\end{array}$

 

Autre méthode : prenons un point $M$ de paramètre $t$ sur $(d)$ ; $$AM^{2}=f(t)=\left(t-\dfrac{1}{3}\right)^{2}+\left(-\dfrac{1}{3}-1\right)^{2}+(t-1)^{2}$$

 

Soit $$f(t)=t^{2}-\dfrac{2}{3}t+\dfrac{1}{9}+\dfrac{16}{9}+t^{2}-2t+1=2t^{2}-\dfrac{8}{3}t+\dfrac{26}{9}$$

 

Le minimum de $f$ est atteint pour $4t-\dfrac{8}{3}=0\ \Leftrightarrow\ t=\dfrac{2}{3}\;,\ $ soit au point $K$ de coordonnées $\left(\dfrac{1}{3}\;;\ -\dfrac{1}{3}\;;\ \dfrac{2}{3}\right)$, et

 

$\begin{array}{rcl} AK^{2}&=&f\left(\dfrac{2}{3}\right) \\ \\ &=&\dfrac{8}{9}-\dfrac{16}{9}+\dfrac{26}{9} \\ \\ &=&2 \\ \\ \Leftrightarrow\ AK&=&\sqrt{2}\end{array}$